RESUMO

Avaliações da função visual são muito complexas por dependerem de mecanismos aferentes, eferentes e cognitivos, além de fatores externos à pessoa examinada, como o tipo de estímulo e o de sua apresentação. O exame da acuidade visual é discutido em seus aspectos formais de definições, quantificações (critérios de medição de um ângulo e tamanho dos optotipos), notações (decimal ou fracionárias), escalas (representando relações angulares, lineares, logarítmicas) e unidades em que os valores são expressos (recíproca do minuto de arco, número puro, freqüência espacial, decibéis e oitavas). Como conseqüência, referências numéricas sobre a acuidade visual e operações que as envolvem (p.ex., cálculo de valores médios, determinação de variações, relações entre elas) podem levar a interpretações muito diferentes e até opostas num mesmo estudo, dependendo dos critérios nele empregados.

Descritores: Acuidade visual; Testes visuais; Testes visuais; Reprodutibilidade de resultados; Campos visuais; Transtornos da visão; Percepção visual; Limiar diferencial

ABSTRACT

Evaluations of the visual function are very intricate since they depend on afferent, efferent and cognitive mechanisms, besides external factors of the examined subject, such as the type of the stimulus and of its presentation. Testing the visual acuity is discussed in its formal aspects related to definitions, quantifications (criteria for the measurements of an angle, size of optotypes), notations (decimal or fractionary), scales (representing angular, linear or logarithmic relationships) and units in which the values are expressed (reciprocal of minutes of arc, pure number, spacial frequency, decibels, octaves). As a consequence, numerical references about visual acuity and respective operations (e.g., calculations of average values, determinations of variations, relationships between them) may lead to very different interpretations of a study, sometimes even opposite, according to the criteria which are used.

Keywords: Visual acuity; Vision tests; Vision tests; Reproducibility of results; Visual fields; Vision disorders; Visual perception; Differential threshold

Acuidade visual. Medidas e notações

Visual acuity. Measurements and notations

Harley E. A. Bicas¹

A avaliação da acuidade visual é, muito provavelmente, o procedimento mais comum entre todos os usados em Oftalmologia. De fato, embora não seja o único dos parâmetros de desempenho funcional do sistema visual, o índice com que se quantifica a capacidade de discriminação de formas e contrastes é o que mais genericamente exprime sua adequação. Diretamente relacionado à transmissão de luz pelas diferentes estruturas oculares, apresenta-se menor, tanto em qualquer dos processos que afetem a transparência delas (nébulas e leucomas corneais, cataratas, opacificações do corpo vítreo), ou impeçam a chegada do estímulo à retina (p.ex., ausência ou ectopia da pupila), quanto na imperfeita formação de imagens pelo sistema óptico ocular (ametropias e aberrações). Basicamente dependente do funcionamento da retina e vias visuais, aparece também reduzida em toda a afecção dessas estruturas (descolamentos, degenerações, inflamações e cicatrizes da parte central da retina, neurites ópticas ou comprometimentos de axônios relacionados às células ganglionares da fóvea, lesões afetando o córtice visual ou outras partes, etc.), ou quando o próprio desenvolvimento das competências neuronais se faz imperfeitamente (ex., ambliopia).

Mas não bastassem todos esses fatores, chamados aferentes, pelos quais atuam estímulo (luz e sua chegada à retina), sensação (a transformação do estímulo em sinal neural), transmissão pelas vias próprias, percepção (a decodificação dos sinais da sensação e sua transformação numa imagem mental) e cognição (o entendimento do significado dessa imagem), a medição da acuidade visual ainda requer uma resposta, subordinada a de elementos eferentes, completando um ciclo de altíssima complexidade. Assim, o registro de um valor de acuidade visual depende não apenas da percepção (cujos componentes são estudados no campo da Oftalmologia), mas também da cognição e de sua resposta (mais comumente investigadas no campo da Psicologia da percepção e da Neurologia), quando afecções como a da agnosia visual (o não entendimento simbólico e semiótico das imagens), a da afasia (o distúrbio de formulação e expressão do pensamento) e a da apraxia (a incapacidade de realização de uma ação desejada) podem comprometer a avaliação e a interpretação do teste realizado.

Em suma: ainda que se costume considerar a tomada da acuidade visual como simples e fácil, não há nessa prova qualquer simplicidade, nem modo de objetivá-la, sem que se levantem sobre o método usado questões de difícil solução. Por isso, até, admite-se o conceito de sua intestabilidade, isto é, o do reconhecimento da impossibilidade de registrá-la, comum ("fisiológica") em crianças pequenas mas presente, também, nas maiores e em adultos, dependendo de estados emocionais (timidez), mentais (retardo no desenvolvimento neuropsicomotor), educacionais (analfabetismo, quando são testadas letras, números ou outros símbolos não aprendidos), etc.

VISÃO: DISCRIMINAÇÃO DE VARIAÇÕES DO ESTÍMULO

Tanto para a iluminação homogênea da retina como para a ausência completa de estimulação visual, embora se possa objetivar entre ambos os casos diferença de resposta bioquímica nas células fotorreceptoras e de sinalização elétrica nos seus axônios ou demais neurônios do sistema visual, há nas duas circunstâncias uma "cegueira" ("luminosa" ou "escura", respectivamente).

Ao contrário, o termo visão é sempre referido para significar a percepção de variação de estímulo luminoso, seja ela temporal (ex., a do aumento homogêneo da iluminação para um olho adaptado ao escuro) ou espacial (ex., o de aparecimento de um ponto de luz num quarto escuro). A distinção temporal entre dois estímulos de mesma intensidade estará condicionada pela capacidade de um fotorreceptor recuperar sua capacidade de resposta ao primeiro, o que corresponde a um período refratário, ou de latência. A transmissão do sinal será então identificada como apresentando uma descontinuidade da freqüência de transmissão ("pulsos") sobre a atividade neural prévia, ou de base. Em termos espaciais, a distinção se faz pela descontinuidade entre campos receptivos estimulados.

Mas, além disso, pode haver, também, uma variação de intensidade entre tais estímulos (temporal ou espacialmente separados), chamada contraste. Assim, os critérios para caracterização da função visual, mesmo no que se refere apenas a uma das qualidades (cores) da luz, são múltiplos e assim seus respectivos testes. Por exemplo, o dos limiares (mínimos) de percepção luminosa, o de adaptação, o da freqüência crítica de fusão de estímulos (estimulação consecutivamente interrompida, um condicionamento temporal), o de formas (estimulação contínua de fotorreceptores espacialmente distanciados), entre os quais o de percepção de alinhamentos (acuidade "vernier", ou hiperacuidade) e o de separações, com ou sem contrastes, etc.

A percepção de formas, aliás, é determinada pelas variações de iluminação (contrastes) entre diferentes áreas da retina, ou por separações espaciais de estímulos de mesma intensidade. No caso da separação espacial de estímulos, admite-se que ela deva ter, no mínimo, a equivalência ao diâmetro de um fotorreceptor foveal (que estaria separando dois outros para que houvesse contraste entre eles; caso contrário, isto é, se não houvesse essa separação mínima entre os estímulos, as suas imagens se fundiriam, dando idéia de continuidade espacial).

Esse tamanho (tradicionalmente estimado como 2 m) relacionado ao segundo ponto nodal do sistema óptico do olho (cerca de 17,2 mm à frente da retina) corresponde a um ângulo de aproximadamente 24²que representa, então, o limite teórico para esse tipo de discriminação, que fundamenta o teste da acuidade visual.

DEFINIÇÃO

Por todas essas razões, não há um consenso sobre como definir acuidade visual, tanto que sua expressão, embora bem entendida e operada por oftalmologistas, costuma trazer embaraços a outros cientistas⁽¹⁾. Geralmente, refere-se acuidade visual como a função (visual) que exprime a capacidade discriminativa de formas; ou como o método com que se mede o reconhecimento da separação angular entre dois pontos no espaço (isto é, distância entre eles, relacionada ao primeiro ponto nodal do olho); ou da resolução (visual) de suas respectivas imagens sobre a retina, relacionadas ao segundo ponto nodal do olho. Nessas "definições", a primeira com ordenação psicobiológica, as outras duas operacionais, não fica claro o que seja "forma" ou "reconhecimento" ou "resolução de imagens". De fato, os próprios conceitos a que tais termos ficam subordinados não são facilmente delimitados. Assim, a resolução visual depende dos níveis diferenciais de iluminação (contrastes) entre as partes do estímulo (por exemplo, entre as tonalidades dos traços de uma figura e as de seu fundo).

Contraste (C) é a relação entre a luminosidade (luminância, refletância) ^(*) máxima (L_M) e mínima (L_m), ou do objeto (L_o) e do fundo (L_f):

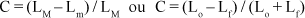
sendo 100% (C = 1 ou ¾1) quando L_o = 1 e L_f = 0, ou vice-versa. De qualquer modo, note-se que o contraste pode ser máximo em diferentes níveis de luminosidade. Ele também varia com o comprimento de onda (cor) da luz incidente.

Aqui se inicia uma parte do problema, já que essa generalização conceitual não é sempre seguida, tornando-se freqüente referir-se acuidade visual às condições de contraste máximo; isto é, à condição de luminosidade (supostamente acima do "limiar de percepção", o que já introduz um fator de "percepção" subjetiva do estímulo) ao lado de uma de "não luminosidade".

Sobretudo, deve-se considerar que o importante não é o contraste do estímulo distal (relações da luminosidade do objeto e de seu fundo) mas do proximal (a luminosidade sobre pontos da retina, depois de sua passagem pelos meios de transmissão da luz, fora e dentro do olho): como é sabido, uma opacificação do cristalino, por exemplo, altera substancialmente a acuidade visual, pela redução dos contrastes.

Assim, a percepção vai, também, depender do tamanho do "objeto" (estímulo), já que aberrações naturais do sistema óptico do olho (esférica, cromática e outras), difrações (relacionadas principalmente ao tamanho pupilar) e ametropias promovem distribuições da luminosidade, sobre a retina, de sorte que as suas transições bruscas entre um ponto e outro são atenuadas: a superposição de luminosidades de uma área mais clara sobre suas vizinhas (e vice-versa) reduz o contraste entre elas. Obviamente, contudo, a luminosidade média dessa região será diferente da de outras partes, podendo facultar ao examinado o entendimento da posição de um acidente do estímulo (por exemplo, a abertura de um anel de Landolt, a "abertura" de uma letra E) embora a correta discriminação das formas não seja possível.

Daí o fato de uma letra ou figura de tamanho grande poder ser percebida, ainda que com borramento de suas margens (atenuação de contraste, por uma ametropia), enquanto a discriminação de uma menor requer "nitidez"; e, ainda, o fato de esta mesma letra (menor), embora nítida, deixar de ser discriminada quando a luminosidade for mais baixa. Por exemplo, na luminosidade de 100 mL (mililamberts), há necessidade de um contraste máximo (100%) para que se discrimine uma separação angular de 30¢¢ (equivalente à AV = 2,00) enquanto se o contraste for de 1% chega-se à separação angular de 20¢ (equivalente à AV = 0,05).

Na prática não há tintas negras que absorvam toda a luz sobre elas incidente (refletância zero) nem papéis brancos que a reflitam totalmente de modo que, estritamente, não há condições concretas de contraste máximo.

QUANTIFICAÇÕES E NOTAÇÕES

A concepção de uma relação inversa para quantificar acuidade visual (V), isto é, a de que ela depende da capacidade de resolução espacial de estímulos, mas que quanto maior a separação angular (a) entre eles (para que se dê a discriminação sensorial), menor o valor que a representa, traz, implicitamente, dificuldades conceituais e operacionais para suas representações numéricas. De fato, os termos de uma relação recíproca (V = a^-1) ficam analiticamente configurados por uma curva assintótica (isto é, que se prolonga até o infinito sem encontrar os eixos das abscissas ou das ordenadas, figura 1a). Mas cuja linearização pode ser tomada com a providência de inverter-se a escala de um dos eixos (por exemplo, o das abscissas, Figura 1b), ou passar a de ambos à escala logarítmica (decimal) (Figura 1c).

MEDIÇÕES DE ÂNGULOS

Um problema prático já é suscitado quando se procura quantificar um ângulo (plano), conceituado como a diferença entre as direções de duas linhas retas (naquele plano). Embora não necessariamente se cruzando, essas duas retas convergiriam para um ponto do espaço, o vértice do ângulo, a partir do qual a medida é feita, por exemplo, com um transferidor. Mas ao serem propostas as relações trigonométricas, tornou-se também possível caracterizar e medir um ângulo por meio de "tamanhos" (h) e "distâncias" (d), considerando-se retas perpendiculares entre si (Figura 2).

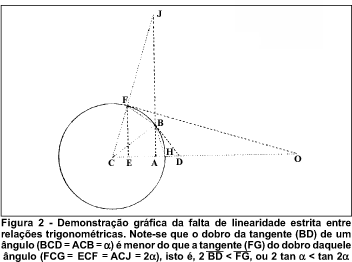
As construções trigonométricas facilitam enormemente o trabalho com ângulos, por suas relações com valores lineares. Por outro lado, essas relações não guardam reciprocidades. Por exemplo, na figura 2 fez-se 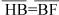de tal modo que os ângulos HCB e BCF sejam iguais (a a).

Nos triângulos ABC e BDC pode-se escrever:

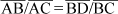
Mas 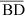é o comprimento da tangente ao círculo (de raio 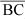) no ponto em que se descreve o ângulo a. Em outras palavras, a relação de 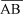(lado oposto ao ângulo) e 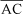(lado adjacente) é igual a (o valor da) tangente do ângulo a, isto é, 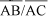= tan a = .

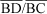Nos triângulos EFC, FGC e AJC pode-se escrever

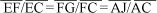
Mas 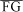é o comprimento da tangente ao círculo (de raio 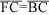) no ponto em que se descreve o ângulo 2a. Assim,

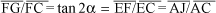
Como 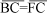vem:

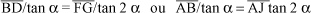
Ora, mesmo visualmente fica fácil notar que 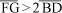ou que 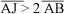e, portanto, tan 2a > 2 tan a. Ou seja, a variação da tangente de um ângulo não é igual à variação dos respectivos ângulos. Assim, por exemplo, tan 35º = 0,700, mas tan 70º = 2,747.

Optotipos e seus tamanhos

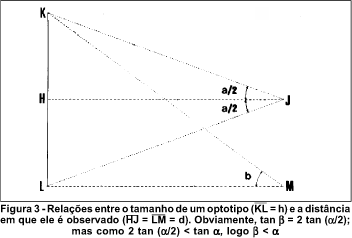
O tamanho de um optotipo (ou, ainda melhor, de seu elemento mínimo pelo qual a acuidade visual que lhe corresponde é definida) deve ser relacionado pela figura 3.

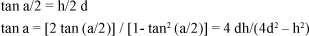
Na verdade, também se considera a definição, bem mais simples:

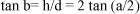
Como não há linearidade entre as tangentes dos ângulos, é óbvio que b e a são diferentes. Inversamente, um dado ângulo (a) deverá corresponder a tamanhos diferentes dos elementos para o teste da acuidade visual (h₁ e h₂) em função das distâncias a que são observados. Assim, os tamanhos totais de optotipos (E₁, E₂, E₃), correspondendo cada um a cinco elementos de ângulo visual a (três barras negras e duas brancas de um optotipo "E" padrão, isto é, 5 h) de acordo a vários conceitos de medidas e arbitrariamente calculados para a distância de 6 metros (= 6000 mm), serão determinados por:

a) No triângulo JHK

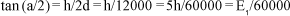
Nessa definição, o tamanho total (E₁ = 5 h) de um optotipo correspondendo à acuidade visual padrão (a = 1¢) será 8,726646321 mm = u₁.

b) No triângulo MLK

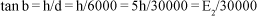
Nessa definição, o tamanho total (E₂=5h) do optotipo correspondendo à acuidade visual padrão (b=1') será 5,726646506 mm = u₂.

Note-se que a diferença absoluta entre u₂ e u₁ é 1,85.10^-10 m = 1,85 Angstrons (na ordem de grandeza do comprimento de onda do raio X) e a relativa igual a 2,12.10^-6 %, equivalendo a uma diferença de menos de um metro (84,8 cm) na circunferência da Terra (40000 km).

c) Pela notação fracionária (6/m ou 20 /p, onde m é o valor da distância em metros e p em pés, à qual o optotipo apresentado deveria ser normalmente visível) há uma proporcionalidade linear entre o tamanho do optotipo (E₃) para a acuidade V e o padrão (u), E₃ = u/V, sendo, entretanto, a acuidade visual fornecida em valores fracionários (V = 20/p)^(**). Portanto, E₃ = u.p/20, onde u é o tamanho do optotipo correspondente à visão normal (u₁ ou u₂). Mesmo para um ângulo de 89º (Tabela II) a diferença de valores de E₃ calculados por um dos padrões (u₁) ou pelo outro (u₂), isto é:

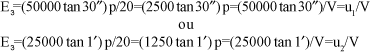
será de 0,8236 mm (isto é, menor do que um milésimo de milímetro).

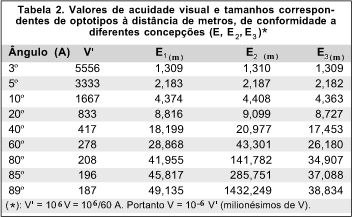
A Tabela 1 mostra as diferenças de tamanhos totais de optotipos (E₁, E₂, E₃) correspondendo a cinco elementos de ângulo visual a ou b, decorrentes dos vários conceitos de medida.

Note-se que mesmo para acuidades visuais muitíssimo baixas (por exemplo, 0,01) a diferença de definição de E₁ para E₂ é praticamente negligenciável, correspondendo a uma variação de 0,02% no tamanho do optotipo (0,154 mm no seu tamanho total). Igualmente desprezíveis são os desvios de cálculo relativos a E₃. Entretanto, para ângulos grandes, os erros são apreciáveis (Tabela 2), passando a diferença de milímetros entre os diferentes conceitos (já dentro de grandeza de um ângulo de 3º, correspondente a uma acuidade de cerca de 0,0056).

Ou, ainda melhor, ao se considerar valores comparativos e não absolutos, acha-se uma diferença de 1% entre E₂ e E₃ (isto é, quando 0,99 E₂ = E₃) para o ângulo A = 9º 54¢ 50,459², isto é, V = 16,81.10^-4 ~ 20/11897.

Para ângulos maiores, fazendo-se V¢ = 10 ⁶ V, sendo V = 1/60 A e passando-se E₁, E₂, E₃ a metros:

Em conclusão, os diferentes critérios de quantificação de tamanhos de optotipos e, ou de medidas de acuidade visual mostram uma concordância muitíssimo grande dentro da faixa de valores costumeiramente empregados. São raros os casos em que se possa quantificar uma acuidade visual menor do que 0,01 pelos métodos tradicionais; e mesmo que isso se tornasse desejável, os resultados práticos não justificariam os cuidados de definições mais, ou menos, rigorosas. Erros em torno de 1% entre formulações só começariam a aparecer em ângulos visuais de cerca de 10º (acuidades da ordem de 1,7.10^-3 ou 20/12000). Assim, dentro da faixa de valores na qual essa diversidade de critérios se aplica, não há diferenças práticas, o que justifica a negligência com que as desuniformidades conceituais sobre a acuidade visual são ainda conservadas.

Mais importante, ainda, é que os valores de E₃, lineares, podem ser considerados proporcionais ao das definições angulares. Desse modo, transfere-se a relação angular de acuidade visual para a de tamanho/distância:

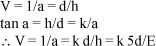
em que k = 2,90888.10^-4; daí V ~ 1,4544. d/1000 E

Para d = 5000 mm, V = 7,272/E

De fato, por essa concepção, a acuidade visual V_F fica definida por:

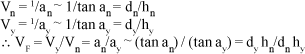
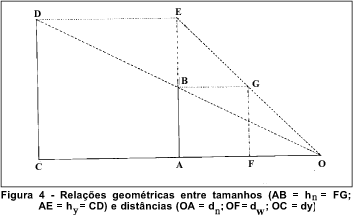
Resulta, pois, que uma relação originariamente angular (a_n/a_y) passa a ser representada por uma linear (a fração de distâncias e, ou tamanhos, d_y h_n/d_n h_y). Nos dois casos, o quociente não tem unidades (é um número "puro") o que suscita a idéia de que os valores sejam absolutamente equivalentes, embora isso não seja verdadeiro. A figura 4 ajuda a esse entendimento.

Por essas duas concepções originam-se os valores de E₁ e E₂ na Tabela 1, baseados respectivamente nos ângulos a e b (Figura 3).

De qualquer modo, fica a possibilidade de se avaliar a acuidade visual a uma distância constante (fazendo-se d_y = d_n) de acordo à variação do tamanho dos objetos testados (optotipos). Desse modo, se tan 1¢ = h_n/d_n e tan a_y = h_y/d_n, isto é, pela Figura 4: d_n = OA (= d_y), h_n = AB, a_n = 1¢, h_y = AE, portanto V_F = AB/AE.

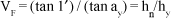
Ou, ao contrário, fixando-se o tamanho do optotipo (fazendo-se h_n = h_y) e verificando-se a distância na qual ele se torna percebido. Se o tamanho fixado (h_n) for o que define a acuidade "padrão" (tan 1¢ = h_n/d_n), vem, pela Figura 4, V_F = (AB/OA) ¸ (FG/OF) = (CD/OC) ¸ (AE/OA) = OF/OA = OA/OC. Portanto:

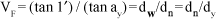
Como a variação de distância implica necessidade de ajustamento focal pelo olho (acomodação), o primeiro processo (variação de tamanho dos optotipos à distância constante) é o mais correto. Mas, paradoxalmente, a notação comumente usada é confusa, sugerindo uma relação de distâncias, como o segundo processo estabelece, embora a acomodação não seja suscitada (como o primeiro requer). Assim, na "clássica" notação dos países de língua inglesa, muito difundida, a acuidade visual padrão é expressa pela relação "20/20", significando isso que d_n = 20 (pés) ou, aproximadamente, 6 metros e h_n = "20", um número arbitrário para definir o tamanho do optotipo, cujas partes equivalem a ângulos de um minuto de arco, a 20 pés. Uma outra acuidade (V_y), definida como 20/200 significa que d_y = 20 (pés), enquanto h_y = 200, quer dizer dez vezes maior do que o padrão (h_n) igual a "20". Em outras palavras, h_y é o tamanho a que um optotipo seria normalmente percebido a 200 pés. Pela figura 4 corresponderia a V_F = OA/OC, isto é, à distância d_y = OA = 20 pés, em que se faz o teste, o optotipo percebido (AE = h_y = CD) deveria ser normalmente visto (sob o ângulo visual a_n) à distância d_n = OC = 200 pés.

A notação fracionária, numericamente, equivale à decimal mas, pela razão de ser mais extensa (o valor da acuidade visual aparece informado pela relação de dois números) torna-se mais informativa. Pelo menos teoricamente, pois o numerador (d_n) deveria expressar a distância à qual a mensuração teria sido realizada. É entretanto comum ouvir-se o relato de "acuidade visual igual a 20/20, tomada a 5 metros", o que se traduz por conhecimento equivocado sobre o assunto. Correta teria sido a referência "5/5"(ou "6/6" se o teste tivesse sido realmente feito a 20 pés...). Na verdade, o uso dessa referência 20/20 para "normalidade" e 20/x para quaisquer outras é condenável pelo que ela supõe como sua unidade referencial de medida (pés): em princípio porque ela não é o padrão de medidas de distância de nosso país, mas sobretudo porque não é o das convenções adotadas internacionalmente (o metro), o que conduz à idéia de que seu uso é inadequado até nos países que se acostumaram a ele.

ESCALAS

Embora todas sejam, fundamentalmente, baseadas no ângulo mínimo de resolução (AMR, ou "MAR, minimal angle of resolution" em inglês), as medidas de acuidade visual podem ser referidas em diferentes escalas, ou representações:

a) Medidas em minutos de arco (a). Nesse caso, as variações (a = AMR) são lineares e inversamente proporcionais à capacidade discriminativa.

b) Medidas na recíproca de AMR, as mais comumente usadas: notações de Snellen (dadas em forma decimal, V = 1/a, ou na fracionária, V_F = 20/20a, com iguais significados). As variações são geometricamente dependentes (caem pela metade conforme ângulos visuais de 1, 2, 4, 8, 16 minutos) mas ficam diretamente relacionadas à capacidade discriminativa.

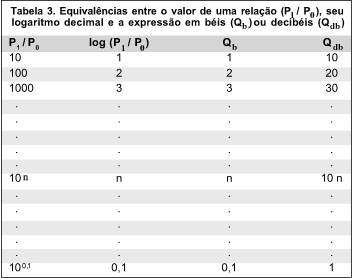
c) Medidas logarítmicas (decimais) do AMR (= log a). Também inversamente proporcionais à capacidade discriminativa, mas mantendo variações numa relação constante (isto é, quando multiplicados ou divididos por um determinado fator, os logaritmos aumentam ou decrescem numa mesma quantidade). Por exemplo, o valor 0,30103, equivalente a log 2, é o que se acresce sucessivamente para achar os valores de a = 2... 4... 8... 16; assim como 0,47712 (equivalente a log 3), é o que se acresce para os valores sucessivos de a = 3... 9... 27...

Essa característica (variação linear numa proporção geométrica que, aliás, é também a da recíproca de a, isto é, escalas de V ou V_F) tem sido muito usada. Uma de suas peculiaridades é a manutenção do mesmo valor numérico, tanto para a expressão de a quanto para a de V (mas, neste caso, com o sinal negativo). Claro, então, que também aparece o sinal "invertido" (negativo para a e positivo para V) com discriminações visuais acima da normalmente convencional (a < 1¢, V > 1,0).

d) Finalmente, a escala de "eficiência visual de Snell-Sterling"⁽²⁾ parte do pressuposto de uma relação progressiva de 83,6% a cada minuto de arco de variação. Essa escala é, pois, exponencialmente decrescente seguindo a fórmula E = 100 e^{-0,179 (a ¾ 1)} em que e é a base dos logaritmos naturais (ou neperianos), e = 2,718281828^(***).

UNIDADES

Mesmo quando apenas relacionada a separações angulares (não se mencionando o contraste), isto é, ao ângulo mínimo de resolução, há diferentes maneiras de exprimir valores de acuidade visual, condições reciprocamente equivalentes⁽³⁾.

a) Recíproca do minuto de arco

Por definição, a acuidade visual (V) é a medida do inverso do ângulo visual (a) com que a pessoa discrimina partes de um objeto (optotipo), ou seja, o ângulo mínimo de resolução (a = MAR).

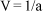
A unidade de ângulo no Sistema Internacional é o grau (º), sendo o minuto (¢) um seu submúltiplo (1º = 60 ¢). A magnitude dos ângulos visuais é da ordem de minutos de arco e assim pode-se dizer que a unidade de acuidade visual é a recíproca do minuto de arco. Poderia ser chamada, por exemplo, de "u". Assim, para discriminação de separações de 1¢ (normal) e de 10¢, ter-se-iam, respectivamente, acuidades visuais de 1 u e de 0,1 u.

b) Número puro

Por outra definição, também muito comum, a acuidade visual (V²) representaria uma relação entre a medida (absoluta) de uma acuidade visual, a_y (isto é, V_y = 1/a_y = y unidades) e a que seria normal, a = 1¢ (isto é, V = 1/a = 1/1¢ = 1 u):

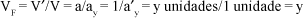
isto é, se o ângulo visual correspondente é a_y = 4¢, V_y = 0,25.

Aliás, a costumeira (mas inadequada) notação "20/20" (para significar V = 1,0), "20/400" (para significar V = 0,05) etc. supõe, tacitamente, uma grandeza sem unidades, pois relaciona duas distâncias: no numerador, a do teste (20 pés); e no denominador a distância em que o optotipo apresentado (e percebido) seria normalmente percebido.

c) Freqüência espacial

Na tomada da acuidade visual, o que se pretende medir é a capacidade de distinguir a separação angular entre dois "pontos" do espaço, cujas imagens na retina se formam em campos receptivos diferentes (na fóvea, o tamanho do fotorreceptor é o do cone). Mas se esses elementos fossem contíguos, a percepção seria a de um único estímulo (maior) e não a de dois, separados. Por exemplo, a percepção de pontos luminosos separados, com imagens formadas em elementos sucessivamente vizinhos é a de uma linha ininterrupta. A "separação" ou descontinuidade corresponde, pois, à existência de um "terceiro" elemento neutro entre os dois estimulados; ou seja, um outro campo receptivo (fotorreceptor, na fóvea) para que se estabeleça o contraste para os dois outros. Em outras palavras, o que importa é a medida (angular) de um elemento entre dois outros (por exemplo, uma faixa escura entre duas claras, que, por suas vezes, supõem outras duas, externas, escuras, para delimitá-las), ou vice-versa, não importando o número de vezes em que isso se repita. Por exemplo, no célebre "E", são cinco as barras, todas de igual medida angular. No optotipo correspondente à acuidade visual igual à unidade, cada uma corresponde ao ângulo visual de um minuto de arco (1¢), mas o tamanho total do optotipo é igual a 5¢. Dada a relativa homogeneidade de distribuição dos campos receptivos, esse padrão é valido tanto para uma direção (horizontal) quanto para outra (vertical).

Ora, a acuidade visual pode então ser medida com mais outros elementos enfileirados, constituindo uma grade, que se define, espacialmente, pelo "comprimento de onda", ou freqüência espacial, com que as alternâncias se sucedem, isto é, pelo número de "ciclos" (ondas, alternâncias).

Assim, o comprimento de onda correspondente à separação angular de uma acuidade visual normal é 2¢ (já que cada barra deve ter a medida de 1¢), o que significa que num grau de arco há 30 "ciclos". Para uma acuidade visual que corresponda ao valor 0,40, a medida das separações é 2,5¢ e portanto o ciclo é de 5¢, o que significa que num grau há 12 desses ciclos. Então:

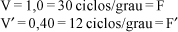
Note-se que F/V = F¢/V¢ = 30; ou seja, basta multiplicar o valor da acuidade visual decimal por 30 para se achar a expressão em ciclos/grau. Ou, ao contrário, dividir essa por 30 para se achar o valor da acuidade visual decimal.

Claro que a freqüência espacial pode vir expressa em ciclos/minuto de arco (F_m). Nesse caso, F_m/V = 0,5: a acuidade visual normal (V = 1) corresponde a 0,5 ciclos/minuto de arco (=F_m); assim, também, V = 0,4 corresponde a 0,2 ciclos/minuto de arco.

Em certos casos, a freqüência espacial é referida não em ciclos/graus (ou ciclos/minutos de arco) mas em ciclos/centímetros⁽⁴⁾. Isso se deve a que, para uma determinada distância, o valor angular pode ser convertido em uma outra medida linear (métrica). Por exemplo: a acuidade visual V = 1,0 corresponde à discriminação de um optotipo E₁ (três barras negras e duas brancas, portanto 2,5 ciclos) de tamanho 7,272 mm (ver Tabela 1); isso pode então ser referido como uma freqüência espacial de 2,5 ciclos/7,272 mm ou 2,5 ciclos/0,7272 cm (= 3,438 ciclos/cm) ou, ainda 2,5 ciclos/0,007272 m (= 343,77 ciclos/m). Obviamente, o tamanho correspondente à acuidade visual normal será diferente a outras distâncias.

Genericamente, as conversões entre acuidade visual em notação decimal (V), ou freqüência espacial (F, em ciclos/grau) e a freqüência espacial em ciclos/cm (= F_c) são dadas em função da distância (d) entre a tela com a grade de barras e o olho por:

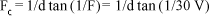
Por exemplo: à distância de 40 cm, a acuidade visual normal (V = 1) é representada por F_c = 42,97 ciclos/cm.

Às vezes pode aparecer referida a unidade "Hertz", mas essa é uma forma imprópria de exprimir freqüência espacial, embora correta para exprimir freqüência temporal (1 Hz = 1s^-1). A representação teoricamente mais apropriada para exprimir freqüência espacial, isto é, o número de ciclos, ou "ondas" (um número "puro", sem unidades) por unidade de comprimento (o metro), eqüivalendo, pois, à recíproca da unidade de comprimento (1 m^-1) é a dioptria, D (1 D = 1 m^-1). Todavia, essas duas formas de expressão de periodicidade, temporal (Hertz) ou espacial (Dioptria) não são dimensionalmente equacionadas às das unidades de ângulos, afinal a grandeza que se pretende medir.

d) Relação logarítmica no sistema decimal ("decibéis")

Ângulos podem ser conceituados como medidas de afastamento direcional entre duas linhas retas, a partir do ponto em que se cruzam; ou como a relação entre dois lados (catetos) de uma figura geométrica formada a partir dessas duas linhas (um triângulo retângulo). Ora, isso pode ser associado ao "bel, b" (por homenagem ao inventor Alexander Graham Bell), uma unidade definida como equivalente ao logaritmo decimal do quociente de duas grandezas, quando a primeira (P₁) é dez vezes maior do que a segunda (P₂). Ou, mais comumente, ao seu respectivo submúltiplo, o decibel, db (1 db = 0,1 b). Lembre-se que essa unidade tem sido convencionalmente aplicada a medidas associadas a movimentos periódicos e para definir intervalos de magnitudes, mas mais especificamente o decibel se associa à medida de níveis de intensidade acústica^(****).

Assim, para uma quantidade em béis (Q_b) igual a y:

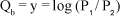
Como 1 decibel = 0,1 b, a quantidade algébrica de decibéis (Q_db) na relação P₁ / P₂, será dada por:

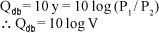
Exprimindo, portanto, uma relação de valores em escala logarítmica, o db (decibel) converte-se numa referência elegante a medidas de acuidade visual.

e) Relação logarítmica no sistema binário ("oitavas")

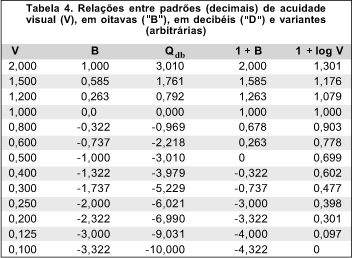
Também por analogia a sons aplica-se a denominação de "oitavas", acima ou abaixo de uma dada freqüência, para significar que uma (oitava) acima, corresponde ao dobro da de uma outra; ou que a freqüência de uma oitava abaixo, é a metade da de uma outra ("cheia")^(*****). Assim, V = 0,50 é a acuidade visual correspondente a "uma oitava abaixo" da normal, e V = 0,25 a "duas oitavas abaixo" da normal, enquanto V = 2,0 representa "uma oitava acima" da normal. V = 0,3 corresponde a uma oitava abaixo da V = 0,6, ou uma acima da V = 0,15. Ora, esse padrão de variação é o de uma escala logarítmica na base 2 (sistema binário), daí podendo se dar uma outra definição a "oitava": o valor de uma unidade de freqüência, medida no sistema numérico binário. Dando-se à acuidade visual padrão (V = 1,0) o referencial para a medida nessa escala logarítmica na base binária ("oitava", B), as relações são dadas pela Tabela IV, conforme a fórmula 2^B = V.

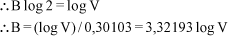
OPERAÇÕES MATEMÁTICAS

Estudos envolvendo valores e variações de acuidade visual ou representações equivalentes (por exemplo, avaliação de um tratamento) suscitam dificuldades operacionais e podem, dependendo da escala empregada nas quantificações, levar a interpretações discrepantes.

Para uma demonstração dessas possibilidades considerar-se-á o valor da acuidade visual no início (V_i) e fim (V_f) da suposta investigação. Realmente, quantificar uma variação pode supor, apenas, conhecê-la absoluta, pela diferença V_f - V_i (melhora, se positiva; piora, se negativa), ou relativizá-la, por exemplo, ao início do procedimento, pelo quociente (V_f - V_i)/V_i ou, então, pelo V_f/V_i.

Mas se uma generalização mais ampla for buscada, com novos questionamentos e respostas, convirá, também, relacionar como parâmetro uma acuidade visual ideal (ou desejável, ou alcançável, etc.), V_e. Seria então possível conhecer-se a limitação do procedimento (pelo estudo da diferença V_f - V_e) e suas eventuais relações com a perda inicial (V_i - V_e) ou com a melhora obtida (V_f ¾ V_i), etc. Na verdade, as combinações são muitas (não se esgotando a totalidade):

a) V_e - V_i, dando a perda total absoluta no início do tratamento;

b) V_e - V_f, dando a perda residual absoluta ao final do tratamento;

c) V_f - V_i, quantificando a melhora total pelo tratamento;

d) V_e/V_i, mostrando a perda relativa, inicial;

e) V_e/V_f, mostrando a perda relativa, final;

f) V_f /V_i, mostrando o ganho relativo com o tratamento;

g) (V_e - V_i) / V_e = 1 ¾ (V_i/V_e), ver "d" e "h";

h) (V_e - V_i) / V_i = (V_e/V_i) - 1, ver "d" e "g";

i) (V_e - V_i) / V_f ou V_f / (V_e - V_i), nível de melhora em função da perda inicial;

j) (V_e - V_f) / V_e = 1 - (V_f/V_e), ver "e" e "l";

k) (V_e - V_f) / V_i, perda residual em função do nível no início do tratamento;

l) (V_e - V_f) / V_f = (V_e/V_f) - 1, ver "e" e "j";

m) (V_f - V_i) / V_e, melhora efetiva relativa ao ideal;

n) (V_f - V_i) / V_i = (V_f /V_i) - 1, ver "f" e "o";

o) (V_f - V_i) / V_f = 1 - (V_i/V_f) ver "f" e "n";

p) (V_e - V_f) / (V_e - V_i), perda residual em função da inicial;

q) (V_f - V_i) / (V_e - V_i), melhora em função da perda absoluta;

r) (V_e - V_f) / (V_f - V_i), perda residual relacionada à melhora;

s) (V_e - V_i) / (V_e - V_f), ver "p";

t) (V_e - V_i) / (V_f - V_i), ver "q";

u) (V_f - V_i) / (V_e - V_f), ver "r";

e outras mais poderiam daí ser tiradas.

Na verdade, há índices mais apropriados que outros. Por exemplo, s, t e u são inversões óbvias de p, q e r, respectivamente. Estes últimos, entretanto, mostrariam valores tanto menores quanto maior a perda inicial (V_e - V_i) e quanto menor a perda residual (p) ou o ganho total (q); ou valores tanto menores, quanto maior o ganho total e menor a perda residual (r). Tais índices, se aplicados à efetividade de um tratamento, mostrariam valores paradoxais (valores menores em tratamentos mais efetivos e vice-versa). Devem, pois, ser evitados, por substituição de suas recíprocas (s, t, u).

Por outro lado, há proporcionalidades entre essas várias relações, cujos significados acabam sendo, basicamente, equivalentes. Por exemplo, supondo-se que se obtenha o valor de uma das três últimas funções (s, t, u) os das duas outras poderão ser derivados. Ou seja, o conhecimento de uma dessas expressões traz implícito o conhecimento das outras. Por exemplo:

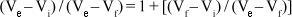
isto é, s = 1 + u.

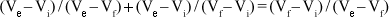
ou seja, s/t = u \ (1 + u)/u = t, ou t = s/(s ¾ 1).

Para demonstração da influência do uso das diferentes escalas na avaliação comparativa de duas condições de tratamento (A e B), consideremos apenas algumas dessas variáveis na análise. Por exemplo, as diferenças (a, b, c) e uma de suas relações respectivas (q). Suponha-se, por exemplo, que se queira estimar a intensidade de uma ambliopia e relacioná-la a um possível ganho após certo tratamento. Seja, então, V_e = 1,0 o padrão a ser alcançado e sobre o qual devam ser medidas as perdas de visão; num caso A, seja V_i = 0,4 a acuidade visual no início de um tratamento e V_f = 0,8 depois de dois meses de um tratamento oclusivo. Dependendo da escala escolhida, variados resultados aparecerão. Um segundo caso (B) deve ser levado em consideração, para comparação com o primeiro; neste, a acuidade visual no início de tratamento (V_i) é 0,1 e ao final do tratamento (V_f) é 0,5. Os cálculos para as escalas de acuidade visual poderiam ser expressos em:

1) valores decimais (V);

2) ângulos mínimos de resolução (a = 1/V);

3) valores logarítmicos do ângulo mínimo de resolução (log a = log V^-1);

4) notação fracionária anglo-saxônica (20/V_F = V);^(******)

5) notação fracionária métrica (6/V_M = V);^(******)

6) freqüência espacial (F = 30V);

7) eficiência porcentual ^(a-1) = 0,8361^(a-1) = E

Mas, obviamente, os significados de V e de F são equivalentes, assim como os de a e V_F V_M ou, pois não só os valores absolutos desses pares repetir-se-ão proporcionalmente (F = 30 V, V_F = 20 a, V_M = 6 a) como suas relações serão absolutamente idênticas.

É claro que, nos dois casos, houve um ganho com o tratamento (V_f ¾ V_i) e que apresenta valores coincidentes em ambos (0,8 ¾ 0,4 = 0,4 = 0,5 ¾ 0,1). Mas como deve ser ele interpretado? Em valores "absolutos" (ou seja, relacionado ao padrão de normalidade, V_e), condição em que eles seriam considerados idênticos? Ou como, eventualmente, considerar um ganho relativo? Em relação ao início do tratamento (V_i), isto é, no primeiro caso 0,4 e no segundo 0,1? À diferença para o que faltaria, ainda, ganhar (V_e ¾ V_f), isto é, no primeiro caso 0,2 e no segundo 0,5?

É óbvio que o critério tomado fará prevalecer conclusões totalmente discrepantes:

a) O ganho foi igual (0,4/1,0 = 0,4/1,0);

b) O ganho foi maior no segundo caso (0,4/0,1, o de início pior) que no primeiro (0,4/0,4);

c) O ganho foi maior no primeiro caso (0,4/0,2), pois faltaria menos para completar o tratamento (0,2) que no primeiro (0,4/0,5), quando ainda faltaria bem mais (0,5).

É possível que ao se apreciar essa questão, a preferência da maioria fique com o critério "b", já que se torna quase intuitivo considerar que (com o critério "a") um ganho de 0,1 a 0,5 ("cinco vezes") não pode ser idêntico a um de 0,4 a 0,8 ("duas vezes"), mas o critério "c" parece também interessante... (Tabela 5)

É de se observar que índices de melhora com o tratamento (V_f ¾ V_i)/V_i, no caso A, são dados como de 100% (para V), 50% (para a), 75,6% (para log a) e 25,1% (para E). Se um outro critério for tomado, como (V_f ¾ V_i)/ (V_e ¾ V_i), as melhoras são, respectivamente, de 66,67%, 83,33%, 75,65% e 81,41%. Ou seja, o melhor índice com o primeiro critério é o pior com o segundo (V). Mas uma constatação é a de que com este critério (q) são mostrados ganhos tanto piores quanto maior a perda inicial (exceto para as medidas do ângulo mínimo de resolução, a), sendo certamente preferível seu inverso. Ou então (V_e ¾ V_i) / (V_e ¾ V_f), isto é, quanto maior a perda inicial e menor a perda residual, melhor o tratamento; ou (V_f ¾ V_i) / (V_e ¾ V_f), quanto maior a melhora e menor a perda residual; ou, ainda, (V_f ¾ V_i)/V_i, quanto maior a melhora e menor a visão discriminativa no começo do tratamento. Curiosamente, todavia, os índices da penúltima e da última coluna não mostram, sempre, as mesmas conclusões. Por exemplo, com o critério da penúltima coluna, as escalas V e E mostram melhores resultados com o tratamento B que com o A, o que também caberia à escala log a (resultado menos negativo). Já com o critério da última coluna dá-se exatamente o inverso.

REFERÊNCIAS

1. Newman M. Visual acuity. In: Moses RA. Editor. Adler's physiology of the eye: clinical application. 6^th ed. St. Louis: Mosby; 1975.         

2. Snell AC, Sterling S. Percentage evaluation of macular vision. Arch Ophthalmol 1925;54:443-61.         

3. Westheimer G. Scaling of visual acuity measurements. Arch Ophthalmol 1979;97:327-30.         

4. Cruz AAV, Rios SS. Acuidade visual. Arq Bras Psicol 1998;50:9-26.         

¹ Professor Titular, Chefe do Departamento de Oftalmologia, Otorrinolaringologia e Cirurgia de Cabeça e Pescoço, Faculdade de Medicina de Ribeirão Preto da Universidade de São Paulo.

Endereço para correspondência: Departamento de Oftalmologia, Otorrinolaringologia e Cirurgia de Cabeça e Pescoço. Faculdade de Medicina de Ribeirão Preto da Universidade de São Paulo - Ribeirão Preto (SP) CEP 14049-900.
Recebido para publicação em 16.01.2002
Aceito para publicação em 05.03.2002

^(*) Certos objetos possuem luminosidade própria (cabendo-lhe os termos iluminação, luminância) enquanto outros apenas a refletem (daí reflexão, refletância).

^(**) A notação 20/p corresponde à distância de 20 pés. Assim, 20 pés 30,48 cm/pé = 6096 mm, para a qual resultaria u₁ = 8,866272663 e u₂ = 8,866272850.

^(***) O valor de e vem de e = 1 + 1^-1 + (1.2) ^-1 + (1.2.3) ^-1 +...+ (1...n) ^-1. Note-se que ln 10 = log_e 10 = 2,302585093.

^(****) O intervalo de um decibel corresponde portanto a uma razão de (aproximadamente) 1,259 entre as intensidades medidas (10^0,1 ~ 1,259). Dez decibéis (um bel) corresponde à relação de grandezas em que uma (P₁) dez vezes maior que outra (P₀). Vinte decibéis (dois béis) corresponde a P₁ = 100 P_o; trinta db correspondem a P₁ = 1000 P_o e assim sucessivamente.

^(*****) Em Música, cada uma das sete notas ("tons") possui uma vibração sonora (freqüência) própria. O intervalo entre duas notas de mesmo nome, isto é, entre a "primeira" (tônica) e a "oitava" (harmônica) dessa escala (chamada diatônica) é definido como o de "uma oitava".

^(******) Note-se que a relação entre as notações fracionárias métrica (baseada em 6 metros) e anglo-saxônica (baseada em 20 pés) não é rigorosamente exata, já que 6 m = 19,685 ft ou 20 ft = 6,096 m. Aliás, 20 ft ou 6 m não são numeradores obrigatórios dessas frações, já que a tomada da acuidade visual pode ser feita a outras distâncias, como por exemplo a de 5 metros, muito usada. A diferença entre a acomodação suscitada para a distância de 6 m (0,17 D) e para a de 5 m (0,20 D) é clinicamente desprezível. Obviamente, todavia, o tamanho de optotipos correspondentes à V = 1,0 será diferente.