
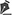
Luis Alberto Vieira de Carvalho1
DOI: 10.1590/S0004-27492008000200013
RESUMO
OBJETIVO: Desenvolver a instrumentação e o "software" para topografia de córnea de grande-ângulo usando o tradicional disco de Plácido. O objetivo é permitir o mapeamento de uma região maior da córnea para topógrafos de córnea que usem a técnica de Plácido, fazendo-se uma adaptação simples na mira. MÉTODOS: Utilizando o tradicional disco de Plácido de um topógrafo de córnea tradicional, 9 LEDs (Light Emitting Diodes) foram adaptados no anteparo cônico para que o paciente voluntário pudesse fixar o olhar em diferentes direções. Para cada direção imagens de Plácido foram digitalizadas e processadas para formar, por meio de algoritmo envolvendo elementos sofisticados de computação gráfica, um mapa tridimensional completo da córnea toda. RESULTADOS: Resultados apresentados neste trabalho mostram que uma região de até 100% maior pode ser mapeada usando esta técnica, permitindo que o clínico mapeie até próximo ao limbo da córnea. São apresentados aqui os resultados para uma superfície esférica de calibração e também para uma córnea in vivo com alto grau de astigmatismo, mostrando a curvatura e elevação. CONCLUSÃO: Acredita-se que esta nova técnica pode propiciar a melhoria de alguns processos, como por exemplo: adaptação de lentes de contato, algoritmos para ablações costumizadas para hipermetropia, entre outros.
Descritores: Topografia da córnea; Córnea; Córnea; Desenho de equipamento; Lentes de contato; Disco óptico; Astigmatismo; Erros de refração; Processamento de imagens assistida por computador; Algoritmos
ABSTRACT
PURPOSE: To develop the instrumentation and software for wide-angle corneal topography using a Placido-based videokeratographer. The objective is to allow the measurement of a greater area of the cornea using a simple adaptation to the Placido mire. METHODS: Using the traditional Placido disc of a commercial corneal topographer, 9 LEDs (Light Emitting Diodes) were installed on the conic mire so that the voluntary patient could gaze in different directions. For each direction Placido images were acquired and processed to form, using a sophisticated computer graphics algorithm, a tridimensional map of the whole cornea. RESULTS: It was shown that up to 100% more area of the cornea may be mapped using the here described technique. We present results for a spherical surface calibration and also for a highly astigmatic cornea and analyze quantitatively the additional area that is recovered in terms of curvature and true elevation. CONCLUSIONS: We believe that this new technique opens opportunities for the improvement of other applications which might benefit from this additional information, such as: contact lens adaptation and design improvement, algorithms for customized refractive surgery, among others.
Keywords: Corneal topography; Cornea; Cornea; Equipment design; Contact Lenses; Optic disc; Astigmatism; Refractive errors; Image processing, computer-assisted; Algorithms
INTRODUÇÃO
O surgimento de técnicas para correção de aberrações oculares, como a ceratotomia radial(1-2) em meados dos anos 80 e o surgimento de lasers para cirurgia refrativa no início dos anos 90(3-4), motivou o desenvolvimento de técnicas mais precisas para a topografia de córnea(5-17), sem falar em instrumentos para ceratometria que já haviam sido desenvolvidos muitos anos antes das cirurgias refrativas, como aquele desenvolvido por Bicas(18) em 1967. Devido a estas necessidades e, ao mesmo tempo, o barateamento dos micro-computadores com processadores mais potentes, surgiram equipamentos sofisticados que automatizaram todo o processo de mapeamento da córnea. Estes instrumentos contêm módulos para processamento das imagens de Plácido e impressão de gráficos coloridos de alta resolução, mostrando a curvatura e elevação em milhares de pontos. Estes instrumentos ficaram conhecidos popularmente como "Topógrafos de córnea" e mais formalmente como videoceratógrafos.
Por vários anos e até os dias de hoje, o videoceratógrafo vem sendo usado com sucesso para triagem pré-cirúrgica em pacientes candidatos a cirurgia refrativa. No entanto, uma das outras grandes promessas destes instrumentos era a melhoria do processo de adaptação de lentes de contato. Para isso as empresas implementaram módulos sofisticados para simulação da adaptação das lentes, permitindo a mudança de vários parâmetros e a visualização de um mapa simulado do padrão de fluoresceína(19). Embora estes módulos tivessem diversos recursos e prometessem economia de tempo na adaptação de lentes rígidas ou gelatinosas, até mesmo em pacientes mais complicados, não foi exatamente isso que ocorreu na prática, especialmente no caso de lentes gelatinosas. Estas lentes têm um diâmetro (aproximadamente 15 mm) bem maior que as lentes rígidas, fazendo com que a região do limbo e esclera seja importante durante a adaptação e para o conforto. No entanto, a topografia de córnea convencional tem amplitude para medir apenas a região central da córnea, mensurando, em média, uma região que varia de 7 a 9 mm em diâmetro. Ou seja, os videceratógrafos convencionais, baseados nos discos de Plácido, não têm condições de medir uma área grande o suficiente para uma simulação fidedigna do processo real de adaptação de lentes de contato gelatinosas. A conseqüência disso é que, durante os anos 90, houve uma grande promessa dos fabricantes e ao mesmo tempo uma grande expectativa dos oftalmologistas, por um sistema que pudesse agilizar e melhorar o processo de adaptação de lentes, mas este objetivo não se concretizou. Junto a isso, esta impossibilidade de mapear o limbo também trouxe conseqüências negativas para os fabricantes de lentes de contato. Para que eles pudessem melhorar o conforto e fluxo lacrimal das lentes, necessitavam de informações de como as lentes se movimentavam na região do limbo, simplesmente indisponíveis nos videoceratógrafos convencionais.
Outra aplicação importante de medidas de maior amplitude da córnea reside nas cirurgias refrativas personalizadas, possíveis apenas recentemente, depois da introdução de lasers capazes de moldar a córnea ponto a ponto (diâmetro do feixe pode chegar a apenas 0,5 mm), denominados "flying-spot" lasers(20-21). Com esta nova tecnologia, as cirurgias refrativas passaram para um segundo estágio de desenvolvimento, de tal modo que não apenas simples miopias simétricas poderiam ser corrigidas, mas também astigmatismos regulares e irregulares, aberrações de ordem mais alta e também hipermetropia. No caso desta última, os algoritmos que calculam a região de retirada de tecido utilizam não somente a região central da córnea mas também as regiões mais periféricas. Isto se deve ao fato de que, para correção de hipermetropia, deve-se gerar uma lente mais abaulada (de maior curvatura) e isso requer uma retirada de tecido maior na periferia do que ao centro da córnea. No entanto, com os atuais videoceratógrafos, conforme mencionado, o mapeamento destas regiões mais periféricas é precário, muitas vezes não permitindo maior precisão dos algoritmos de planejamento da ablação, os quais necessitam de informação na região periférica para poder calcular uma transição suave entre região ablada e região não ablada(22-26). Com a técnica introduzida aqui, será demonstrado que pode-se ter um mapeamento suficientemente abrangente para que estes novos algoritmos de ablação para cirurgia de hipermetropia possam ser utilizados com maior precisão e eficiência. Além do planejamento pré-cirúrgico, passa-se a ter dados mais abrangentes para o estudo e acompanhamento do processo de cicatrização da região operada.
Embora outros sistemas de topografia, que utilizam tecnologias alternativas à de Plácido, existam no mercado, há limitações evidentes. O Orbscan tem sido utilizado em algumas clínicas, mas existem trabalhos mostrando que é um instrumento de baixa reprodutibilidade em alguns casos específicos(27). O Pentacam(28) é uma grande promessa pois, ao invés de utilizar uma fenda vertical em varredura horizontal, utiliza uma fenda que rotaciona centrada no ápice da córnea. Isso garante uma maior precisão e reprodutibilidade do sistema, permitindo um mapeamento preciso de regiões periféricas até o limbo. No entanto, este sistema ainda é novidade e está fase de estudos por diversos colegas pesquisadores; além disso, seu custo é ainda um tanto alto por ser uma tecnologia ainda nova.
MÉTODOS
Captura das imagens
Utilizamos um topógrafo de córnea Eyetec modelo CT4000 com modificações em "hardware" e "software" para realizar este trabalho. Foi instalado na parte de trás dos discos de Plácido um conjunto de 8 LEDs na cor branca (Figura 1). Estes LEDs são controlados por um circuito eletrônico simples, que permite ao operador que acenda-os ou apague-os. Ao acender os LEDs o operador deve pedir ao paciente que fixe o olhar em cada um dos LEDs, inclusive o central que já existe nos equipamentos de série, para que possa então digitalizar cada uma das imagens de Plácido. Conforme o paciente fixa o olhar em cada um dos LEDs, há um movimento de rotação e translação do olho, de tal maneira que o reflexo dos discos de Plácido também ocorre em uma diferente região da córnea (Figura 2).
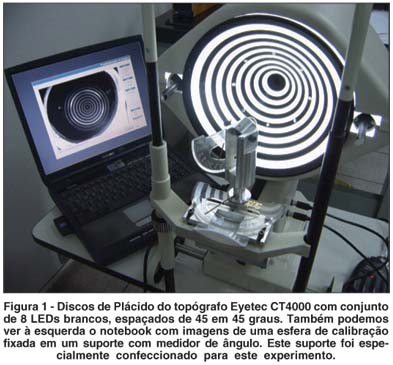
Na figura 2 observa-se primeiramente a imagem convencional da córnea (0), mostrando o reflexo frontal dos discos de Plácido. Nas outras 8 imagens (de 1 a 8) pode-se ver nitidamente a distorção dos discos de Plácido conforme o paciente fixa o olhar em diferentes LEDs periféricos.
Processamento de imagens
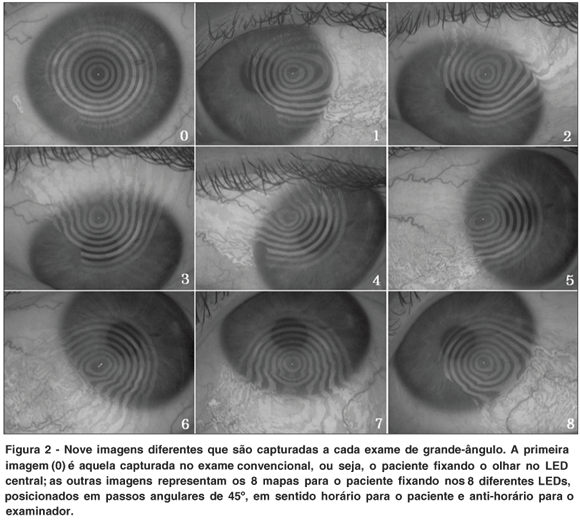
Para o processamento de imagens mostradas na figura 2 foi utilizado o mesmo módulo de processamento da versão comercial do aparelho(29-32). Cada uma das imagens mostradas na figura 2 foi digitalizada e depois processada. Como exemplo mostramos na figura 3 a imagem número (1) da figura 2 durante o processamento.
Como se pode perceber os discos de Plácido foram detectados com bastante eficiência até as regiões próximas ao limbo. No entanto, quando os discos de Plácido são refletidos em regiões próximas à interface limbo-esclera, aumenta-se a irregularidade dos mesmos. Devido à perda de especularidade, o reflexo tende a ser menos uniforme nesta interface, formando discos muito distorcidos e, ao migrar-se para a região de esclera, torna-se praticamente impossível o processamento de imagens e detecção das bordas. Portanto, para a esclera é virtualmente impossível utilizar os algoritmos de cálculo de curvatura e elevação(33). No entanto, como veremos mais adiante, a região mapeada depois da junção das 9 imagens, é significativamente maior do que na videoceratografia convencional e representa praticamente toda a córnea, até a interface limbo-esclera.
Cálculo das elevações dos mapas central e periféricos
Para realizar o cálculo das elevações de cada ponto detectado no passo anterior, utilizamos algoritmos documentados na literatura(34-35), portanto não iremos entrar aqui em detalhes a respeito deste processo. O que é importante mencionar aqui é que os resultados são salvos em matrizes contendo coordenadas cilíndricas, ou seja, a tripla ordenada (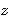 ,
, 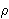 ,
, 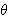 ). Após o cálculo de cada conjunto para cada uma das nove posições do olho, transformamos as coordenadas cilíndricas em cartesianas, através das simples equações:
). Após o cálculo de cada conjunto para cada uma das nove posições do olho, transformamos as coordenadas cilíndricas em cartesianas, através das simples equações:

onde a coordenada z não precisa de transformação pois é a mesma que nas coordenadas cartesianas.
Após esta transformação de coordenadas, passa-se a realizar uma transformação geométrica, associada com as rotações e translações do olho para cada um dos mapas mostrados na figura 2. Estas transformações são necessárias para garantir que todos os pontos mensurados estejam no mesmo referencial.
Transformação de coordenadas
Para compreensão da metodologia utilizada para implementação do algoritmo implementado neste trabalho é essencial que o leitor compreenda o princípio e as equações envolvidas na transformação de todos os pontos do mapa periférico para o sistema de coordenada central. Para ilustrar esta metodologia, na figura 4 temos alguns diagramas que demonstram o princípio básico das transformações geométricas de translação e rotação em apenas duas dimensões.
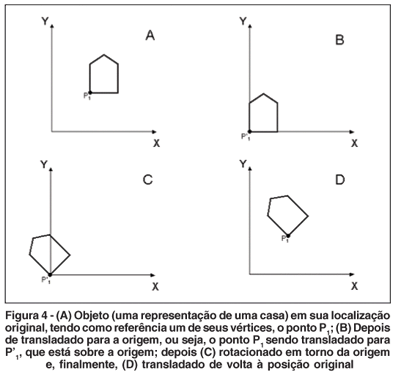
Como podemos ver pela figura 4A, temos inicialmente um objeto cujas coordenadas (x, y) de todos os pontos são conhecidas. Vamos supor que desejamos rotacionar este objeto (como exemplo aqui, o formato de uma casa) em torno de um de seus vértices, representado aqui pelo ponto P1. Para que esta tarefa de transformação seja possível, temos que, inicialmente, transladar o objeto para o centro do sistema de coordenadas. Esta operação de translação está representada pela figura 4B. Depois podemos aplicar a operação de rotação em torno de P'1. Desta maneira percebemos que nestas operações há um princípio interessante em que a operação de rotação deve ter seu eixo de rotação centrado na origem (Figura 4C). Finalmente, após a rotação desejada, o objeto pode ser novamente transladado de volta para a localização original, mas desta vez com todas os seus pontos rotacionados em torno do ponto de referência original P1 (Figura 4D).
Para aplicarmos estes mesmos princípios no olho humano as operações são análogas, mas matematicamente um pouco mais complexas por envolver desta vez o espaço tridimensional e não apenas bidimensional. Para isso nos basearemos no diagrama da figura 5.
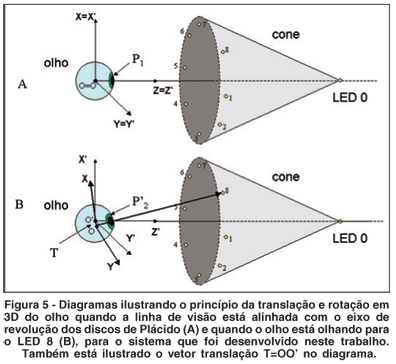
Chamaremos de referencial principal, denotado aqui por (X, Y, Z), aquele que tem como referência o olho, ou seja, podemos dizer que este referencial está estático com relação ao olho (Figura 5A). Isso quer dizer que, mesmo para rotações ou translações do olho, este referencial não sofre mudanças pois ele está "acoplado" ao olho. Podemos também afirmar que o eixo Z deste sistema coincide com a linha de visão do paciente. É neste referencial que se deseja realizar todas as medidas de elevação e curvatura da córnea, para todas as posições do olho quando fixando o olhar para cada um dos 9 LEDs.
Já o referencial do videoceratógrafo, representado aqui por (X', Y', Z'), e diferente daquele do olho, tem como eixo Z o eixo do sólido de revolução representado pelo cone onde estão pintados os discos de Plácido, e também no centro do qual está o LED central (LED 0), caracterizando este eixo também como eixo óptico do videoceratógrafo. Pela figura 5A pode-se perceber que, na situação corriqueira, naquela em que o olho está fixando olhar sobre o LED central, os dois sistemas de coordenadas são coincidentes, ou seja, (X, Y, Z)=(X', Y', Z') e portanto todos os pontos mensurados em um sistema de coordenadas são idênticos aos pontos mensurados no outro, e vice-versa.
Agora analisemos uma situação diferente, em que o olho passa a fixar olhar sobre um ponto que não está sobre o eixo Z do topógrafo, ou seja, um ponto periférico, situado em algum lugar sobre o cone dos discos de Plácido (Figura 5B). Nesta situação o cone continua estático com relação ao seu eixo próprio de coordenadas (X', Y', Z') e o mesmo acontece com o olho (X, Y, Z). No entanto, as medidas realizadas pelo aparelho estão sempre no eixo de coordenadas do aparelho, sendo que as medidas que queremos realizar no olho têm que estar sempre no sistema referencial do próprio olho. Desta maneira temos que realizar a transformação das coordenadas dos pontos no referencial do cone para o referencial do olho.
Como exemplo mostramos, na figura 5A, um ponto qualquer mensurado na córnea P1= (X1, Y1, Z1) onde também vale P1= P1'= (X1', Y1', Z1'), ou seja, como não há translação e nem rotação do olho com relação ao cone, ambos os referenciais são idênticos e portanto as coordenadas medidas em um referencial são exatamente iguais às coordenadas medidas no outro referencial, ou seja, X1= X1', Y1= Y1', Z1= Z1', e este fato vale para todos os milhares de pontos mensurados sobre a córnea. Já para uma situação em que há rotação e translação do olho (Figura 5B), um ponto P2 medido no referencial do olho não tem mais as mesmas coordenadas do mesmo ponto quando do ponto de vista das coordenadas do cone, ou seja, P2¹P2', de tal maneira que X2¹X2', Y2¹Y2', Z2¹Z2'. Mas quando se mede qualquer ponto sobre a córnea lembre-se, como mencionamos anteriormente, o videoceratógrafo sempre usa o seu próprio sistema de coordenadas (X', Y', Z'), sendo que, como também já mencionado, utiliza-se sempre o sistema de referencial do olho para imprimir e visualizar dados da topografia da córnea, ou seja, o sistema (X, Y, Z). Desta maneira, quando há uma translação e rotação do olho, para que as medidas do topógrafo possam ser utilizadas de maneira correta, é necessário que os pontos passem por uma transformação geométrica para que estejam com as novas coordenadas no sistema de coordenadas do olho e não do videoceratógrafo. Este processo pode ser representado matematicamente como:

onde K representa a matriz de transformação. Como temos translação e rotação de um sistema de coordenadas com relação ao outro, é necessária a concatenação das transformações, que pode ser representada por:

onde T representa a matriz de translação e R representa a matriz de rotação.
A translação total de um eixo com relação ao outro pode ser representada pelo vetor T= OO', o qual pode ser visto na Figura 5(B). Podemos também representar o vetor translação 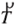 como sendo a soma do deslocamento em cada direção dos eixos cartesianos, ou seja:
como sendo a soma do deslocamento em cada direção dos eixos cartesianos, ou seja:
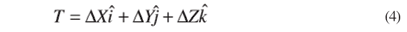
ou seja, onde cada um dos termos em delta representam as respectivas translações em cada direção, que são então multiplicados pelos vetores unitários (versores i, j e k) em cada uma destas direções. Para compreender como se calcula cada um destes componentes podemos nos basear no digrama da figura 6.
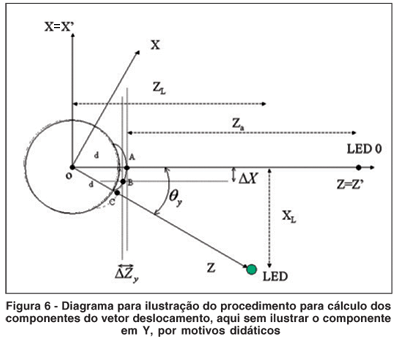
O diagrama da figura 6 ilustra duas situações distintas: primeiro aquela em que as coordenadas do olho são as mesmas do videoceratógrafo, portanto não havendo rotação ou translação; segundo, a situação em que o olho rotacionou de um ângulo q em torno do eixo Y (para olhar para o LED 3, por exemplo). Nesta situação o videoceratógrafo terá que deslocar de DZy para focalizar corretamente o instrumento, pois o ápice na posição anterior (ponto A) passou para uma nova posição (ponto B), não sendo mais localizado no ápice original depois de rotacionado (ponto C). Da figura pode-se determinar, fazendo-se a aproximação de que o novo ápice (ponto B) está a meio caminho em termos de rotação total do olho (do ponto A para o ponto C), sendo então o deslocamento dado por:
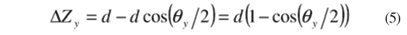
sendo que este deslocamento na direção Z representa somente a contribuição devida à rotação em torno do eixo Y; para computar a contribuição deste deslocamento em termos da contribuição em torno do eixo X, quando houver, basta realizar uma conta análoga, mas agora utilizando a metade do valor do ângulo de rotação em torno do eixo X. Somadas estas contribuições tem-se o componente de translação total em Z, ou seja:

para ser utilizado na equação (4). Agora falta computar os componentes de translação em X e Y. Mas pela figura 4 fica fácil de ver que

e

e tem-se portanto todos os componentes do vetor translação (equação (4)).
Agora precisa-se determinar quais as rotações envolvidas, para que se possa encontrar a forma da matriz R. Não é difícil imaginar quais são estes ângulos. Basta pensarmos no sistema de referencial do oho (X, Y, Z) como sendo estático e imaginar que é o cone do videoceratógrafo que rotaciona. Como o cone não rotaciona em torno do eixo Z, ou seja, não estamos considerando a ciclotorção do olho, pode-se descartar qualquer rotação em torno deste eixo; agora, para posicionar o cone em diferentes direções, pode-se perceber que bastam rotações seqüenciais em torno do eixo X e Y, para cada LED. Vamos representar estes dois ângulos como qx e qy. Dados estes dois ângulos de rotação em torno dos dois eixos conhecidos, a matriz de rotação R pode ser representada como:

onde
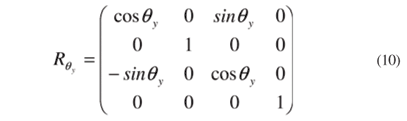
e
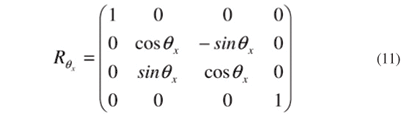
de tal maneira que a multiplicação destas matrizes leva à matriz total de rotação
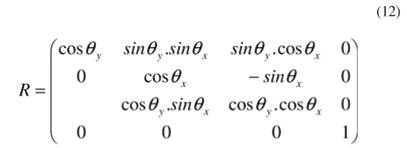
que é a matriz que representa a concatenação das rotações para cada eixo. Isto significa que, sabendo-se calcular os ângulos de rotação qx e qy ter-se-á qual o valor das coordenadas de cada ponto mensurado no referencial do topógrafo no referencial do olho, e com isso ter-se-á então mapeado uma região bem maior da córnea, que é o objetivo principal deste trabalho.
Como pode-se ver, faz-se necessário o conhecimento dos ângulos qx e qy . Usando o diagrama da figura 5 fica mais fácil compreender estes cálculos, que serão demonstrados aqui apenas para o ângulo qx. A figura 5 representa um olho que está fixando o olhar sobre um LED cujas coordenadas (XL, YL, ZL) com relação ao sistema de coordenadas do cone (X', Y', Z') são muito bem conhecidas. Fazendo-se a aproximação de que o centro de rotação do olho (Zrc, na figura 5 representado por d) é estático e conhecido e que o videoceratógrafo, através de suas câmeras laterais, fornece a distância do ápice da córnea até o LED (Za), podemos escrever:

onde

Analogamente, para o outro ângulo temos

ou seja, ambos os ângulos necessários são possíveis de serem determinados, desde que se conheça a posição de cada LED no cone e ao mesmo tempo a distância destes até o ápice da córnea e também fazendo-se as aproximações que já mencionamos. Como as dimensões do cone são perfeitamente conhecidas, assim como a posição dos LEDs, a câmera lateral do aparelho fornece a informação necessária para se computar a posição do ápice.
Aproximação da superfície da córnea por polinômios de Zernike
Aplicando-se a transformação de rotação descrita pela equação (12) a cada conjunto de pontos relativo a cada mapa, utilizando-se os valores de ângulos computados utilizando-se as equações (13) e (15), chega-se a uma matriz completa que inclui todos os pontos mensurados, sendo que agora todos eles têm coordenadas (x, y, z) relativas ao eixo de coordenadas central, ou seja, o eixo de coordenadas do olho. Estes pontos esparsos descrevem todos os pontos examinados sobre a superfície da córnea anterior.
O próximo passo é a interpolação ou aproximação destes pontos por alguma curva ou conjunto de polinômios, de tal maneira que sua representação fique mais compacta e evite a sobreposição de pontos. No entanto, esta técnica precisa ser suficientemente precisa para que seja capaz de descrever as pequenas nuanças e ao mesmo tempo mudanças mais intensas em curvatura e elevação em córneas mais distorcidas. Como demonstrado anteriormente(36) há duas técnicas bastante comuns aplicadas a este problema e que fornecem resultados satisfatórios: aproximação por Polinômios de Zernike ou interpolação por Série de Fourier. Neste caso específico será aplicado o método dos Polinômios de Zernike, pois há interesse não apenas na forma da córnea como também em suas aberrações ópticas, caso específico em que os coeficientes de Zernike são mais propícios. Para maiores detalhes relativos às características específicas destes polinômios favor consultar(37-38), entre outros.
Para representar cada córnea como uma somatório de Polinômios de Zernike fizemos uma aproximação dos dados de elevação do topógrafo Zc (r, q) e passamos a representá-la como uma somatória destes polinômios. Usando um sistema de coordenadas cilíndrico, representamos a elevação pela letra Zc e as coordenadas da borda de um certo ponto sobre um dos discos de Plácido pelo par ordenado r, q, como mostrado no esquema da figura 7.
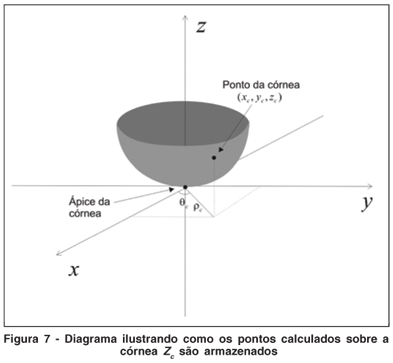
Desta maneira a superfície da córnea pode ser representada pela somatória:
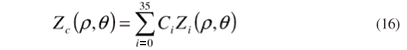
Para encontrar os coeficientes Ci utilizamos o método dos mínimos quadrados. Para tal minimizamos o termo:
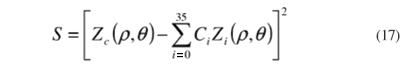
onde o termo à esquerda dentro do colchete representa a elevação da córnea obtida através do videoceratógrafo e o termo à direita representa a somatória de cada Polinômio de Zernike (Zi) multiplicado por seu respectivo coeficiente (Ci). Como pode ser visto, estamos utilizando os 36 primeiros termos de Zernike, embora estes polinômios possam ser gerados até a ordem que se desejar(38). A utilização dos primeiros 15 termos não é uma imposição nossa, é apenas o número comumente sugerido na literatura para aproximações de dados referentes às aberrações do olho e que podem também ser perfeitamente utilizadas para descrever a topografia da córnea(36).
Para minimizar o termo S da equação (17) aplicamos a primeira derivada com relação a todos os coeficientes e igualamos a zero (ponto de mínimo):

Quando fazemos isso montamos um sistema linear de equações que pode ser descrito por

onde A é a matriz dos termos de Zernike calculados nos pontos (r, q) considerados, B é a matriz dos dados de elevação obtidos pela topografia de córnea e C é o vetor que contém os coeficientes de Zernike desejados. Aplicando-se um simples método de inversão de matrizes, como o método de Gauss, por exemplo, chegamos aos valores destes coeficientes para cada córnea considerada. A partir deste ponto os dados da córnea central e dos 8 mapas periféricos estão "fundidos" em um único mapa de pontos e portanto prontos para serem analisados como um todo. A seguir apresentamos nossos resultados preliminares para uma esfera de calibração e uma córnea in vivo.
RESULTADOS
Foram inicialmente realizadas medidas em uma esfera de calibração com raio de curvatura de 7,73 mm. Esta esfera de vidro foi fixada em um suporte especialmente construído para este fim (veja figura 1), de tal maneira que os mesmos ângulos de rotação que ocorrem para o olho humano foram simulados para esta esfera. O objetivo principal de se realizar inicialmente medidas em uma esfera foi verificar se o algoritmo estava funcionando, pois para a esfera conhecemos de antemão tanto o raio de curvatura como a elevação, algo que não ocorre no caso de olhos in vivo.
Como exemplo, na figura 8 podemos ver um mapa 3D das elevações das nove regiões de topografia da esfera depois de implementadas as operações de translação e rotação nos pontos dos discos de Plácido, descritas nas seções anteriores.

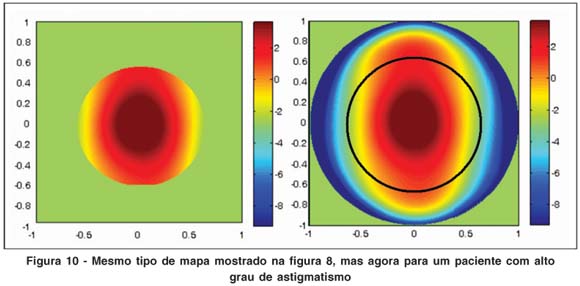
Na figura 9 podemos ver as mesmas superfícies, mas agora impressas na forma de um mapa plano das elevações codificadas por cor, onde a escala de elevação está em mm e os eixos X e Y estão normalizados (1 unidade corresponde a 6 mm). A região originalmente medida por um videoceratoscópio convencional, que equivale à nossa região central, está delineada artificialmente nos mapas de grande-ângulo.
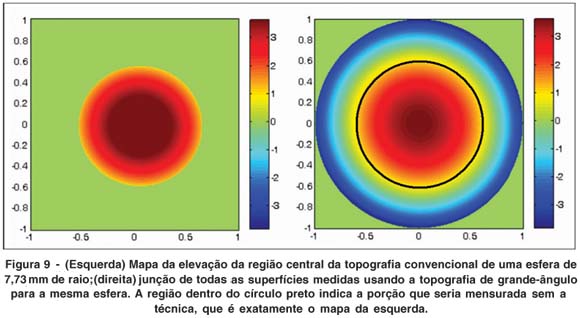
Esta análise mostrou que o algoritmo estava funcionando, pois tanto os gráficos de elevação quanto de curvatura estavam coerentes, mostrando uma continuidade coerente com o esperado. O erro quadrático médio (EQM) da superfície calculada por topografia convencional comparado aos valores teóricos de elevação para uma esfera de 7,73 mm de raio foi 0,2 micrômetros, o mesmo valor obtido com o novo sistema de grande-ângulo. Estes valores indicam que o algoritmo que realiza a fusão dos mapas estava funcionando satisfatoriamente, pois os erros são da mesma grandeza que para topografia central. Isso significa que o processo de rotação e translação, mesmo com as aproximações mencionadas nas seções anteriores, possibilita resultados precisos.
Com estes exames preliminares na esfera de calibração pode-se constatar que o sistema estava, portanto, pronto para ser testado em córneas humanas in vivo. Para isso escolhemos, para esta análise preliminar, uma córnea com alto grau de astigmatismo. Na figura 10 podemos ver os mesmos tipos de mapas que foram impressos para a esfera, mas desta vez para o paciente com astigmatismo.
DISCUSSÃO
Ainda são necessárias medidas em superfícies mais complexas e com contorno conhecido e cuidadosamente controlado para que a real precisão do algoritmo seja conhecida em superfícies diferentes de esferas perfeitas. Isto ocorre porque, mesmo para topografias convencionais, somente usando a imagem central, quando se mede uma superfície esférica, os erros dos algoritmos que calculam elevação são menores do que quando se está se medindo superfícies como ceratocone, por exemplo. Somente após este passo poderemos realizar medidas em uma população in vivo estatisticamente significativa e portanto concluir se a técnica é realmente reprodutível para o olho humano (para isso mediremos o mesmo olho várias vezes) e se esta técnica realmente tem aplicações práticas.
Após este passo poderemos realizar medidas em uma população estatisticamente significativa, contendo vários formatos diferentes de córneas (ceratocone, astigmatismo, pós-PRK, pós-LASIK, pós-ceratoplastia, pós-ceratotomia radial, etc) e averiguar a utilidade da técnica em termos práticos, ou seja, se os dados extras colhidos pela topografia de córnea de grande-ângulo realmente contribuem para melhorias em outros procedimentos, dentre eles a adaptação de lentes de contato, os algoritmos para ablação em cirurgias personalizadas para correção de hipermetropia, entre outras aplicações.
CONCLUSÃO
Finalmente, tanto o Pentacam quanto o Orbscan, principalmente pelo fator custo e também devido a propriedades intelectuais das técnicas, que são recentes, existem em muito menor quantidade que os videoceratógrafos baseados em discos de Plácido, cujo princípio tem mais de 100 anos. Neste sentido acredita-se que a técnica introduzida aqui tenha a chance de beneficiar um número muito maior de oftalmologistas, pois necessitam de mudanças muito simples no hardware dos topógrafos, sendo a maior parte do sistema implementada em software, bastando um up-grade para instalar um módulo à parte. Também acreditamos que esta técnica possa ser utilizada por todos os fabricantes, pois a maioria usa princípios similares para fabricação dos discos de Plácido.
REFERÊNCIAS
1. Cherry PM, Britton R. Experimental radial keratectomy in rabbits for the correction of aphakia. Cornea. 1984;3(1):61-4.
2. van Setten GB, Salonen EM, Vaheri A, Beuerman RW, Hietanen J, Tarkkanen A, et al. Plasmin and plasminogen activator activities in tear fluid during corneal wound healing after anterior keratectomy. Curr Eye Res. 1989;8(12):1293-8.
3. Binder PS. Corneal epithelial and stromal reactions to excimer laser photorefactive keratectomy. III. The excimer laser and radial keratotomy: two vastly different approaches for myopia correction. Arch Ophthalmol. 1990;108(11):1541-2.
4. McDonnell PJ, Garbus JJ, Salz JJ. Excimer laser myopic photorefractive keratectomy after undercorrected radial keratotomy. Refract Corneal Surg. 1991;7(2):146-50.
5. Schor P. Idealização, desenho, construção e teste de um ceratômetro cirúrgico quantitativo. [tese]. São Paulo: Universidade Federal de São Paulo; 1997.
6. York MA, Mandell RB. A new calibration system for photokeratoscopy. II. Corneal contour measurements. Am J Optom. Arch Am Acad Optom. 1969; 46(11):818-25.
7. Klyce SD. Computer-assisted corneal topography, high resolution graphics presentation and analysis of keratoscopy. Invest Ophthalmol Vis Sci.1984; 25(12):1426-35.
8. Koch DD, Foulks GN, Moran CT, Wakil JS. The corneal EyeSys System: accuracy, analysis and reproducibility of first-generation prototype. Refract Corneal Surg. 1989;5(6):424-9.
9. Mammone RJ, Gersten M, Gormley DJ, Koplin RS, Lubkin VL. 3-D corneal modeling system. IEEE Trans Biomed Eng. 1990;37(1):66-72.
10. Belin MW, Litoff D, Strods SJ, Winn SS, Smith RS. The PAR Technology Corneal Topography System. Refract Corneal Surg. 1992;8(1):88-96.
11. Carvalho LA, Tonissi SA, Castro JC. Preliminary results of a computerized Placido disc surgical corneal topographer. In: 9º SPIE Conference on Ophthalmic Technologies, San Jose, California. 1999. p.53-62.
12. Carvalho LA, Paranaguá R, Santos LE, Tonissi AS, Romão AC, Oliveira AC, Yasuoka FM, Castro JC. Desenvolvimento de um instrumento computadorizado para avaliação da curvatura da córnea humana. Rev Fís Apl Instrum. 1997;12(3):81-90.
13. Carvalho LA, de Faria e Souza SJ, Castro JC. Desenvolvimento de um sistema para medida da curvatura da córnea durante o ato cirúrgico. Rev Fís Apl Instrum. 1996;11(3):119-26.
14. Ventura L, Sousa SJ, Masili M, Santos LE, Vieira LA, Castro JC. Desenvolvimento de um "Software" para a determinação automatizada da miopia, hipermetropia e astigmatismo oculares. Rev Fís Apl Instrum. 1996; 11(2):77-83.
15. Carvalho LA, Tonissi SA, Romão AC, Santos LE, Yasuoka F, Oliveira AC, et al. Desenvolvimento de um instrumento computadorizado para medida do poder refrativo da córnea (videoceratógrafo). Arq Bras Oftalmol. 1998;61(4):640-54.
16. Carvalho LA, Tonissi AS, Castro JC. Preliminary tests and construction of a computerized quantitative surgical keratometer. J Cataract Refract Surg. 1999; 25(6):821-6. Comment in: J Cataract Refract Surg. 2000;26(8):1104-5.
17. Carvalho LA, Romão AC, Tonissi S, Yasuoka F, Castro JC, Schor P, et al. Videokeratograph (VKS) for monitoring corneal curvature during surgery. Arq Bras Oftalmol. 2002;65(1):37-41.
18. Bicas HEA. Sobre um novo princípio de ceratometria (e da sua aplicação através de um instrumento servindo também a outras finalidades, adaptável aos biomicroscópios) [tese]. Ribeirão Preto: Universidade de São Paulo; 1967.
19. Jani BR, Szczotka LB. Efficiency and accuracy of two computerized topography software systems for fitting rigid gas permeable contact lenses. CLAO J. 2000;26(2):91-6.
20. Stojanovic A, Nitter TA. 200 Hz flying-spot technology of the LaserSight LSX excimer laser in the treatment of myopic astigmatism: six and 12 month outcomes of laser in situ keratomileusis and photorefractive keratectomy. J Cataract Refract Surg. 2001;27(8):1263-77.
21. Doga AV, Shpak AA, Sugrobov VA. Smoothness of ablation on polymethylmethacrylate plates with four scanning excimer lasers. J Refract Surg. 2004;20(5 Suppl):S730-3.
22. Vinciguerra P, Epstein D, Azzolini M, Radice P, Sborgia M. Algorithm to correct hyperopic astigmatism with the Nidek EC-5000 excimer laser. J Refract Surg. 1999;15(2 Suppl):S186-7.
23. Alpins NA, Taylor HR, Kent DG, Lu Y, Liew M, Couper T, et al. Three multizone photorefractive keratectomy algorithms for myopia. The Melbourne Excimer Laser Group. J Refract Surg. 1997;13(6):535-44.
24. Shimmick JK, Telfair WB, Munnerlyn CR, Bartlett JD, Trokel SL. Corneal ablation profilometry and steep central islands. J Refract Surg. 1997;13(3): 235-45. Comment in: J Refract Surg. 1997;13(3):215-8.
25. Schwiegerling J, Snyder RW. Corneal ablation patterns to correct for spherical aberration in photorefractive keratectomy. J Cataract Refract Surg. 2000; 26(2):214-21.
26. Schwiegerling J, Snyder RW. Custom photorefractive keratectomy ablations for the correction of spherical and cylindrical refractive error and higher-order aberration. J Opt Soc Am A Opt Image Sci Vis. 1998;15(9):2572-9.
27. Basmak H, Sahin A, Yildirim N. The reliability of central corneal thickness measurements by ultrasound and by Orbscan system in schoolchildren. Curr Eye Res. 2006;31(7-8):569-75.
28. Uçakhan OO, Ozkan M, Kanpolat A. Corneal thickness measurements in normal and keratoconic eyes: Pentacam comprehensive eye scanner versus noncontact specular microscopy and ultrasound pachymetry. J Cataract Refract Surg. 2006;32(6):970-7.
29. Carvalho LA, Bruno OM. Técnicas diferentes para análise de imagens de Plácido podem melhorar precisão da videoceratografia. Arq Bras Oftalmol. 2005;68(6):797-805.
30. Carvalho LA. A simple and effective algorithm for detection of arbitrary Hartmann- Shack patterns. J Biomed Inform. 2004;37(1):1-9.
31. Bruno OM, Plotze RO, Carvalho LA. Algoritmo para processamento de imagens da retina in vivo com aplicações na biometria. Scientia. 2004;15(2):13-21.
32. Carvalho LA, Romão AC. Instrumentação para digitalização e processamento computacional de imagens da pupila in vivo. Rev Fís Apl Instrum. 2003; 16(1):24-9.
33. Klein SA, Corzine J, Corbin J, Wechsler S, Carney T. Wide angle cornea-sclera (ocular) topography. [serial on the Internet] Proc SPIE. 2002[cited 2006 Oct 21];4611. Available from: http://cornea.berkeley.edu/pubs/157.pdf
34. Klein SA. Corneal topography reconstruction algorithm that avoids the skew ray ambiguity and the skew ray error. Optom Vis Sci. 1997;74(11):945-62.
35. Klein SA. Axial curvature and the skew ray error in corneal topography. Optom Vis Sci. 1997;74(11):931-44.
36. Carvalho LA. Accuracy of Zernike polynomials to characterizing optical aberrations and the corneal surface of the eye. Invest Ophthalmol Vis Sci. 2005;46(6):1915-26.
37. Carvalho LA, Castro JC. Preliminary results of an instrument for measuring the optical aberrations of the human eye. Braz J Phys. 2003;33(1):140-7.
38. Born M, Worf E. Principles of optics: electromagnetic theory of propagation, interference and diffraction of light. 7th ed. Cambridge: Cambridge University Press; 1999.
Endereço para correspondência:
Grupo de Óptica, Instituto de Física de São Carlos
Universidade de São Paulo
Av. Trabalhador Sãocarlense, 400 - Cx. Postal 369
São Carlos (SP) CEP 13560-970
E-mail: [email protected]
Recebido para publicação em 16.09.2006
Última versão recebida em 02.11.2007
Aprovação em 22.11.2007
Trabalho realizado no Laboratório de Óptica Oftálmica, Grupo de Óptica do Instituto de Física de São Carlos da Universidade de São Paulo - USP - São Carlos (SP) - Brasil.
Nota Editorial: Depois de concluída a análise do artigo sob sigilo editorial e com a anuência do Dr. Waldir Martins Portellinha sobre a divulgação de seu nome como revisor, agradecemos sua participação neste processo.
O trabalho apresentado está sendo patenteado junto ao INPI (Instituto Nacional de Propriedade Intelectual).