Survival analysis is a non-parametric statistical model in which the dependent variable is the “time interval” and the independent variable is the “occurrence or not” of a given event^(1-4). The analysis measures and compares the lapsed times from interventions or exposures to given “events.” Understanding the concept of median survival, the time interval in which the event occurs in 50% of participants, is essential. The median survival has a similar meaning to that of the means and standard deviation used in classical descriptive statistics. Kaplan-Meier curve estimators are named after the creators of this broadly used method in medicine⁽⁵⁾ that estimates the probability of survival, under different conditions and at different time intervals with a graph that illustrates the probability over time.

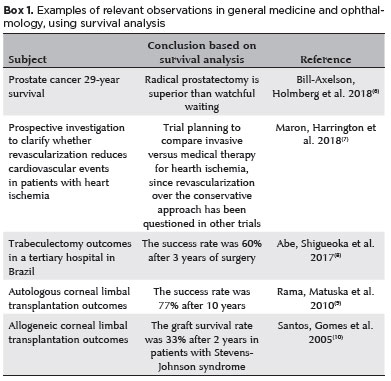
In medicine, survival analyses are used to predict the longevity of surgical interventions such as fistulas or transplants, as well as the longevity of disease-free or complication-free periods in various forms of chronic diseases and malignancies (Box 1). Survival analyses are excellent for evaluating outcomes and helping to make therapeutic decisions anticipating progressions. These analyses may be applied in comparative longitudinal studies on the safety and efficacy of clinical or surgical treatments.

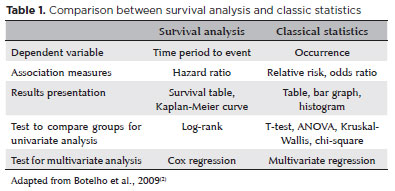
Survival times measure the time interval from a starting point until the occurrence of a given event (e.g., death, cure, relapse, incubation, or equipment failure). Table 1 shows a comparison between the possible outcomes of survival analysis and classical statistics⁽³⁾ when applied to the same problem. Crucially, survival analysis values the whole curve and not isolated points.

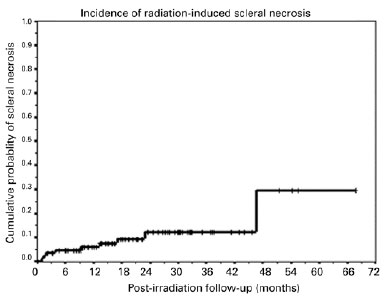
Over long follow-up periods, events for some participants may occur before the analysis period. Moreover, many participants get lost to the follow-ups because they leave the study for different reasons (e.g., participants migrate to another city) or the study may end before the event occurs (events may occur after the study period, but research is expensive, and it needs to have a start and a deadline). While in a classic per protocol analysis the above participants get excluded, in survival curve analyses, they are designated as censored⁽¹¹⁾. If the event happens before the analysis time period, they are censored “on the left,” and if the event does not occur even after the analysis period has ended, they are censored “on the right.” If participants are lost to follow-up in the middle of the study, they constitute the interval censorship (the participant’s time interval until the event cannot be accurately measured). Censored data are represented by crosses or other marks in the graphic presentation (Figure 1). Censorship must follow the basic premise of not being related to prognosis, because if some of the censored individuals in one of the groups have diseases so advanced that they should not be in the study, this will generate a selection bias. Another important assumption is that the prognosis should be the same for all participants, as the characteristics of participants at the beginning and end of the inclusion period must be similar to avoid another selection bias.

Figure 1. Kaplan-Meier cumulative probability curve showing the incidence of radiation-induced scleral necrosis (SNEC)⁽¹²⁾.

One of the advantages of survival analysis is that it considers both data from participants who develop the event and data from those who are censored and can compare survival medians between different groups when the event occurs in at least 50% of the participants.

The comparisons between groups are based on two variables: the survival time interval and the status at the end (occurrence or not of the event or censorship). In the Kaplan-Meier method, the follow-up time is divided into intervals, with limits corresponding to the follow-up time between events, with or without censorship. The likelihood of participants at the beginning of each interval to develop the event by the end of each interval is estimated. Survival at the end of each interval equals the product of cumulative survivals to the end of the previous interval by conditional survival in that interval. Individuals censored in one interval no longer count as individuals at risk in the next interval (Table 2).

In survival analyses, groups are compared using some tests: In the log-rank test, the null hypothesis (H0) is that no difference between the survival curves of the two groups exists. If the test shows a P-value <0.05, H0 is rejected and the alternative hypothesis (H1) is accepted, assuming a statistical difference between the groups. Confidence intervals can also be calculated. Hazard is the probability that any participant, who did not have the event, will have it at that time. The hazard ratio compares the instantaneous incidence of events in the different groups and is estimated by the Cox regression test. The ratio estimates the relative risk of developing a particular event within a time interval. The Cox’s proportional hazards are used when the aim is to analyze predictive factors (covariates) that may be interfering with survival.

Care should be taken when interpreting the survival curve in relation to the sample size. For example, from the first censored participant, the survival curve becomes an estimate, so estimates in the final observation periods are quite inaccurate due to the reduction in the number of participants. Another crucial point is proportionality, that is, hazards must be proportional at different time intervals. If the percentage of censorship is asymmetric, caution should be exercised when interpreting results. For example, when comparing two types of cancer treatment, one treatment may have more events (deaths) at the beginning but longer survivals at the end, while the other may progress with better survival at the beginning and more events at the end, showing a disproportionality of events over time, for both groups.

Survival analyses are good for analyzing data behavior over time, the Kaplan-Meier curve estimates the survival curve (descriptive statistics), the log-rank test compares two survival curves, the hazard ratio is a mea sure of association (similar to relative risk), and the Cox regression allows analysis of the influence of predictive factors (covariates). Thus, survival analyses are one of the most scientifically accurate methods to preview the future among all the imperfect approaches.

REFERENCES

1. Bewick V, Cheek L, Ball J. Statistics review 12: survival analysis. Crit Care. 2004;8(5):389.

2. Botelho F, Silva C, Cruz F. Epidemiologia explicada-análise de sobrevivência. Acta Urol. 2009;26(4):33-8.

3. Rich JT, Neely JG, Paniello RC, Voelker CC, Nussenbaum B, Wang EW. A practical guide to understanding Kaplan-Meier curves. Otolaryngol Neck Surg. 2010;143(3):331-6.

4. Bland JM, Altman DG. Survival probabilities (the Kaplan-Meier method). BMJ. 1998;317(7172):1572-80.

5. Kaplan EL, Meier P. Nonparametric estimation from incomplete observations. J Amer Statist Assoc. 1958;53(282):457-81.

6. Bill-Axelson A, Holmberg L, Garmo H, Taari K, Busch C, Nordling S, et al. Radical Prostatectomy or Watchful Waiting in Prostate Cancer - 29-Year Follow-up. N Engl J Med. 2018;379(24):2319-29.

7. Maron DJ, Harrington RA, Hochman JS. Planning and Conducting the ISCHEMIA Trial. Circulation. 2018;138(14):1384-6.

8. Abe RY, Shigueoka LS, Vasconcellos JPC, Costa VP. Primary Trabeculectomy Outcomes by Glaucoma Fellows in a Tertiary Hospital in Brazil. J Glaucoma. 2017;26(11):1019-24.

9. Rama P, Matuska S, Paganoni G, Spinelli A, De Luca M, Pellegrini G. Limbal stem-cell therapy and long-term corneal regeneration. N Engl J Med. 2011;363(2):147-55.

10. Santos MS, Gomes JAP, Hofling-Lima AL, Rizzo LV, Romano AC, Belfort Jr R. Survival analysis of conjunctival limbal grafts and amniotic membrane transplantation in eyes with total limbal stem cell deficiency. Am J Ophthalmol. 2005;140(2):223-30.

11. Prinja S, Gupta N, Verma R. Censoring in clinical trials: review of survival analysis techniques. Indian J Community Med Off Publ Indian Assoc Prev Soc Med. 2010;35(2):217.

12. Correa ZM, Huth B, Augsburger JJ. Scleral necrosis in patients with posterior uveal melanomas evaluated by transcleral fine needle aspiration biopsy and treated by 125I plaque. Arq Bras Oftalmol. 2018;81(4):330-5.

Submitted for publication: December 10, 2019.
Accepted for publication: December 16, 2019.

Funding: This study received no specific financial support.

Disclosure of potential conflicts of interest: None of the authors have any potential conflicts of interest to disclose.