INTRODUCTION
He who faces the challenge of learning visual optics is often tortured by questions that the concept of ray bundles fails to answer, such as: Why does a divergent bundle of rays becomes parallel at infinity? Why does the angular aperture of a diverging bundle not measure its vergence? What is the meaning of vergence? Is it a measure of curvature or power? While the answers to these questions have been determined, they are not readily accessible. Instead, they are scattered throughout the literature left by brilliant astronomers and mathematicians over the centuries. The objective of this paper is to compile the answers to some of these questions and in the process, introduce some concepts underexplored in texts of visual optics.
Light
"The night was so dark we could see nothing". This sentence of everyday life straightforwardly unveils one of the most basic facts of visual optics: there is no vision without light. For an object to be viewed, it has to send out light. The light needs not to be self-generated; it may be reflected from another source. When it strikes the eye it is deflected by the cornea and crystalline lens to form an upside-down image on the retina. There, it is converted into nerve impulses that are sent to the occipital cortex, where they become a visual impression. To achieve good vision, all the events involved in the transmission of visual information, from the light source to the occipital cortex, have to occur faultlessly. Visual optics is specifically concerned with those factors that influence the quality of retinal images.
It is remarkable that this sequence of events had already been described by the French mathematician René Descartes in 1637(1-3). His intuition was so accurate that his views on this subject were only recently revised(3-6).
Light sources
Light sources are sites of light. They can be luminous or non-luminous. The former emit their own light, such as the sun, light bulbs, and fire(7). The latter simply reflect received light. They include either the irregular surfaces of ordinary objects that reflect light diffusely (balls, shoes, paintings), or images of lenses and curved mirrors.
In 1604 Johannes Kepler, a German astronomer, postulated that an extended object can be interpreted as composed of myriads of points, each acting as a source point of light(8,9). When light is refracted by a lens, the final image represents the sum of the refractions of each of these points. This assumption greatly simplified the study of optics, since instead of analyzing the refraction of all points of an object, one has only to choose a representative one and generalize the findings.
The point of a source taken as a reference is called an object point when it emits light, and an image point when it receives light. For instance, the image formed by a lens is composed of image points that receive the refracted light. However, if these image points are chosen to provide light to a second lens, they become object points to this lens.
Every object point is linked to an image point and vice versa. They become conjugated by refraction of light the same way two people become related by marriage. The distance from the lens to the object point is called the object distance and the distance from the lens to the image point is called the image distance. Since the lens is the associative agent, distances are measured from it.
Wavefronts
In 1801 Thomas Young(10-12), an English scientist, established the wave theory of light, which had been formulated in the seventeenth century by the Dutch astronomer Christiaan Hoygens(13,14). In this approach, any object point emits spherical waves with convex wavefronts. As the wave train moves away from its' source it expands, becoming ever less curved (Figure 1A). The distance of the wavefront to the object point is the object distance. It is also its radius of curvature. The reciprocal of this distance is the curvature of the wave surface. Representing the object distance (or the radius of curvature) by u and the curvature of the wavefront by U, the relation between them is:
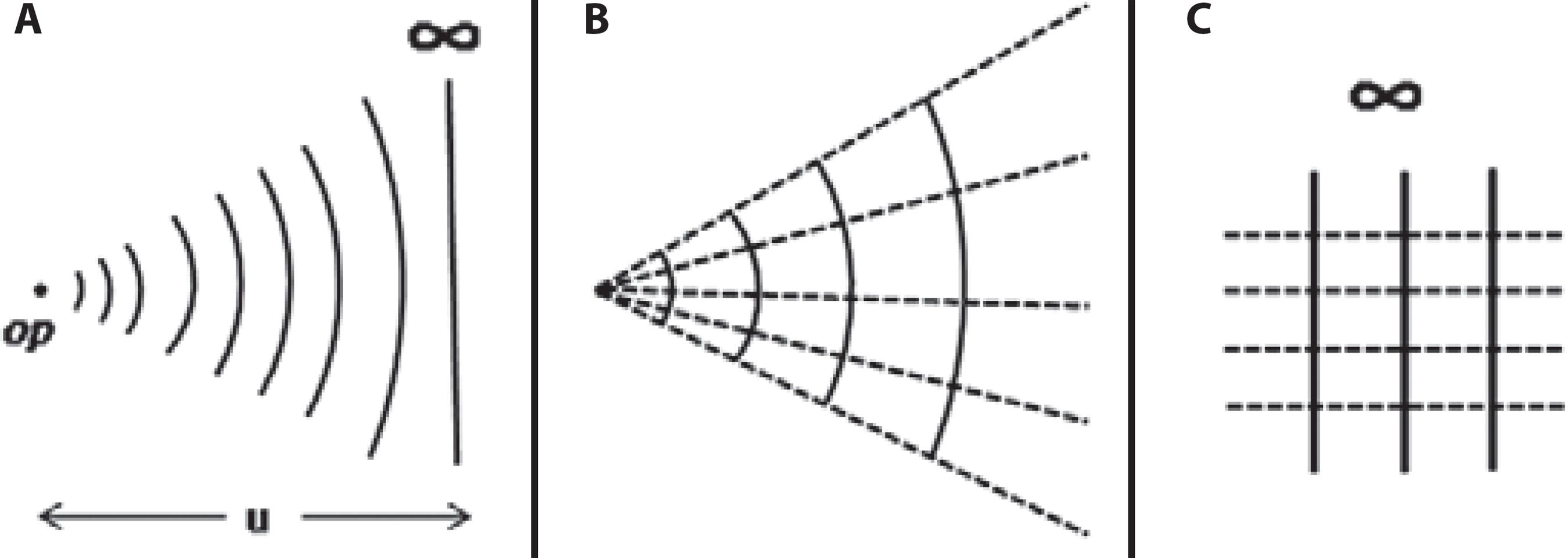
Figure 1 Waves and rays. A) Diverging convex wavefronts; op: object point; u: object distance. B) A diverging bundle of rays (dashed lines) perpendicular to curved wavefronts (the rays form the figure of a fan). C) Flat waves at infinity (solid vertical lines) generating a bundle of parallel rays, perpendicular to the wavefronts (dashed lines).
By convention, convex wavefronts are diverging surfaces with negative curvatures. If a wavefront is diverging, one must replace u in Formula 1 with a negative number.
When the distance from the wavefront to the object point approaches infinity, the curvature of the wave surface approaches 1/∞, or zero. A wavefront with zero curvature is flat (Figure 1A).
When a lens modifies the curvature of an incoming wavefront as a result of refraction, an exiting wavefront is created along with a new source of light that is linked to it. This new source is called an image point. This is especially important because it becomes the reference point for the refracted wave train.
If the wavefront that strikes the lens is flat, the image point is unique, because it is conjugated to the infinity. In this special case, any curvature showed by the exiting wavefront is due to the lens (Figure 2). The image point conjugated to the flat wavefront receives the distinguished name of focus.
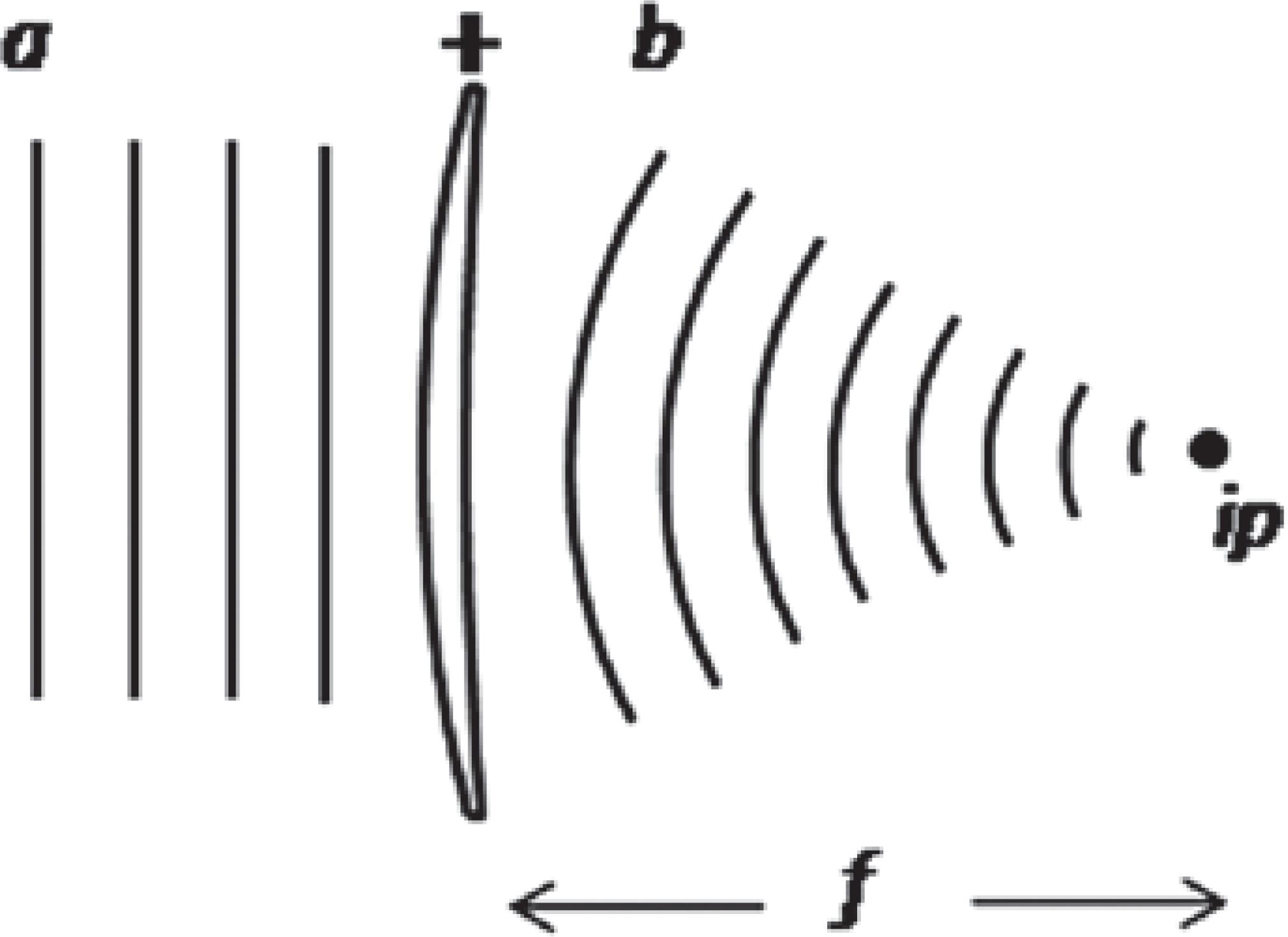
Figure 2 Refraction in a convex lens. ip: real image point, which is also the focus of the lens, because the light comes from infinity; f: real focal distance; a and b are respectively flat and concave wavefronts.
The distance from the lens to the focus is the focal length. The reciprocal of this variable stands for the bending capability of a lens placed in a vacuum or in air. Representing this variable by F and the focal lens by ƒ, the relation between them is:
If the profile of the wavefront that emerges from the lens is concave, ƒ is positive; if convex, ƒ is negative.
Real object points do not emit concave wavefronts. These wave-fronts are generated by the refraction of light trough convex lenses. Once created, they converge to an image point. On their way, they bend and contract gradually until they become a single point (Figure 3). The distance from the lens to the image point is the image distance. It is also the radius of curvature of the refracted wavefront at the lens plane. Representing the image distance by v and the curvature of the wavefront by V, the relation between them is:
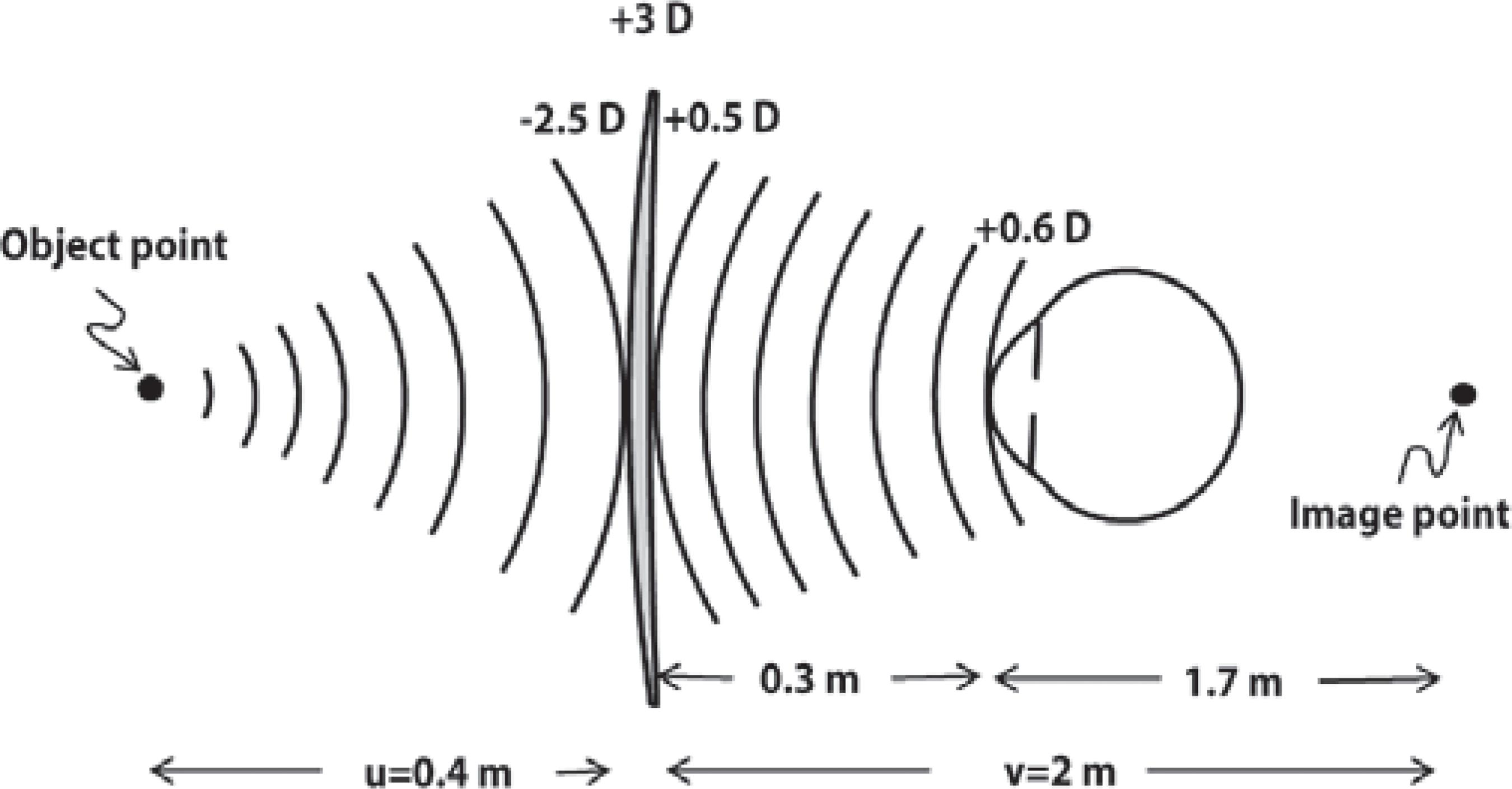
Figure 3 Refraction of light through a + 3 D lens. u: object distance; v: image distance; 0.3 m: distance from the lens to the corneal plane.
By convention, concave wavefronts are converging surfaces with positive curvatures. If a wavefront is converging, we must replace v in Formula 3 with a positive number.
Curvature and radius of curvature
From a geometrical standpoint, u, ƒ, and v are the radii of curvature of spherical surfaces. The reciprocals of these distances are the curvatures of the corresponding surfaces(15). The unit of measurement of curvature is the meter(16). In visual optics, it is a common practice to express curvature in diopters (D)(17). Technically, this is not a unit of curvature, but of vergence. This metaphorical extension is probably derived from the perception that curvatures and vergences are numerically identical in air. Thus, a wavefront placed 0.4 m to the right of an object point will have a curvature of 1/-0,4 = -2,5 D (Figure 3). The distance is negative because real objects always emit diverging waves. If this distance were given in another unit, it would have to be converted to meters to allow for the use of the diopter.
Vergence of light
The light propagated from a point object loses curvature evenly as it moves toward infinity. Lenses can modify the natural course of propagation by refraction. As previously mentioned, the resulting wavefront breaks its link to the original source and joins another source: the image point (Figure 3).
The vergence of a lens is the power it has to modify the curvature of a wavefront, and the vergence of a wavefront is the power it has to resist the lens action. The result of the refraction depends on the interplay between these two powers. The interaction is positive when the lens increases the curvature of the wavefront, and is negative when it decreases or inverts it.
Vergence, either of a lens or a wavefront, increases with the curvature of the surface and with the optical density of the medium the light travels through. Numerically, the vergence of a surface is the product of the curvature and the index of refraction of the medium (n). Vergence is also measured in diopters (D).
The optical density of the medium through which the light travels increases vergence by increasing the compression of the wave trains(18). Compressed waves (with shorter wavelengths) are less liable to further compression by a lens, which makes them less compliant to the lens action. In other words, compressed wave trains have more energy to sustain their natural course(19). This is also the reason why blue light has more vergence than red light: the former is more compressed than the later.
When the index of refraction is close to the unit (n ≅ 1), as in a vacuum or air, vergences and curvatures become numerically interchangeable. Yet this does not mean they are identical. Curvature measures the bending of a surface, while vergence measures the effect of the bending on the refraction. Wavefronts with the same radius of curvature in different media have the same curvature but different vergences. Even authorities in visual optics occasionally make mistakes in this regard(20).
By convention, the vergence of a diverging or convex wavefront is negative and the vergence of a converging or concave wavefront is positive. For lenses, the rule is different. Convex surfaces are positive because they add convergence to the refracted light, while concave surfaces are negative because they add divergence to the refracted light.
The following formula expresses the relationship among vergences of the object, its image, and the lens, for a homogeneous medium:
Formula (4) shows that the vergence of the image point (Vn) is the sum of the vergences of the object point (Un) and of the lens (Fn). It can be rewritten in terms of radii of curvature, as follows:
Note that in a vacuum or in air, where n ≅ 1, the above formula is nothing more than the composition of Formulas 1 to 3. It is known as the Gaussian form of the Thin lens formula for a homogeneous medium(21), named after the German mathematician Carl Friedrich Gauss(22,23). A thin lens is one in which the thickness is irrelevant when compared to its focal length(24).
Working with vergences
Let's picture an object point placed at 0.4 meters to the left of a +3 D lens and an eye placed 0.3 m to the right of it, as shown in figure 3. What is the vergence of the light when it strikes the eye?
Since nothing has been stated otherwise, we may assume that the medium is air, with n=1. The vergence of the object point as it strikes the lens is 1/-0.4 = -2.5 D. To remind us that our vergence measurements take place at the lens plane, we write a "-2.5 D" on the diagram just to the left of the lens, where the incoming wave is(25). The vergence of the exiting wavefront, found using Formula 4, is + 0.5 D. This is written just to the right of the lens to again remind us that it is accessed at the lens plane. The image distance, given by Formula 3, is 1/0,5 D or 2 m.
Our problem is to find the curvature of the refracted wavefront at the corneal plane, multiply it by the index of the medium (n=1) and arrive with the vergence at this plane (Figure 3). The curvature we are looking for is the reciprocal of the distance from the corneal plane to the image point. This is found by subtracting the distance of the lens to the cornea (0.3 m) from the image distance (2 m). The result is: 2 m-0.3 m = 1.7 m. The reciprocal of this value equals 1/1.7 m or 0.6 D. This is the vergence of the light when it strikes the eye.
You may find it intriguing that the vergence of concave wave-fronts increase as they depart from a lens. This is not as obvious as the weakening in vergence of diverging waves. The difficulty is caused by our natural, but inappropriate, tendency to locate the wavefront with respect to the lens, instead of to its source. It turns out that as the concave wavefront travels away from the lens it comes closer to its source, the image point. Since the wavefront loses vergence when it moves away from a light source, it should not be surprising that it gains vergence when it moves toward it. Thus, the gain in vergence is not due to the departure from the lens, but to the proximity to the image point.
Ethereal light sources
We have stated that a refracted wavefront breaks its link to the original source and becomes associated with an image point. Ideally, this is true only when the refracted wave has a concave configuration. If it has a convex configuration, it continues to diverge infinitely and does not associate to any real image point. However, if the train of diverging waves is prolonged retrogradely it will produce the impression of emanating from a point located on the side of the incoming rays (Figure 4). This imaginary point is called the virtual image point. It cannot be projected on screens due to its absence of substance. However, it can be visualized by the brain or a sensor, via interpolation of the data contained in the wave train. Virtual image points are typical of, but not exclusive to, negative lenses. With the appropriate optical system, it is also possible to create virtual object points.
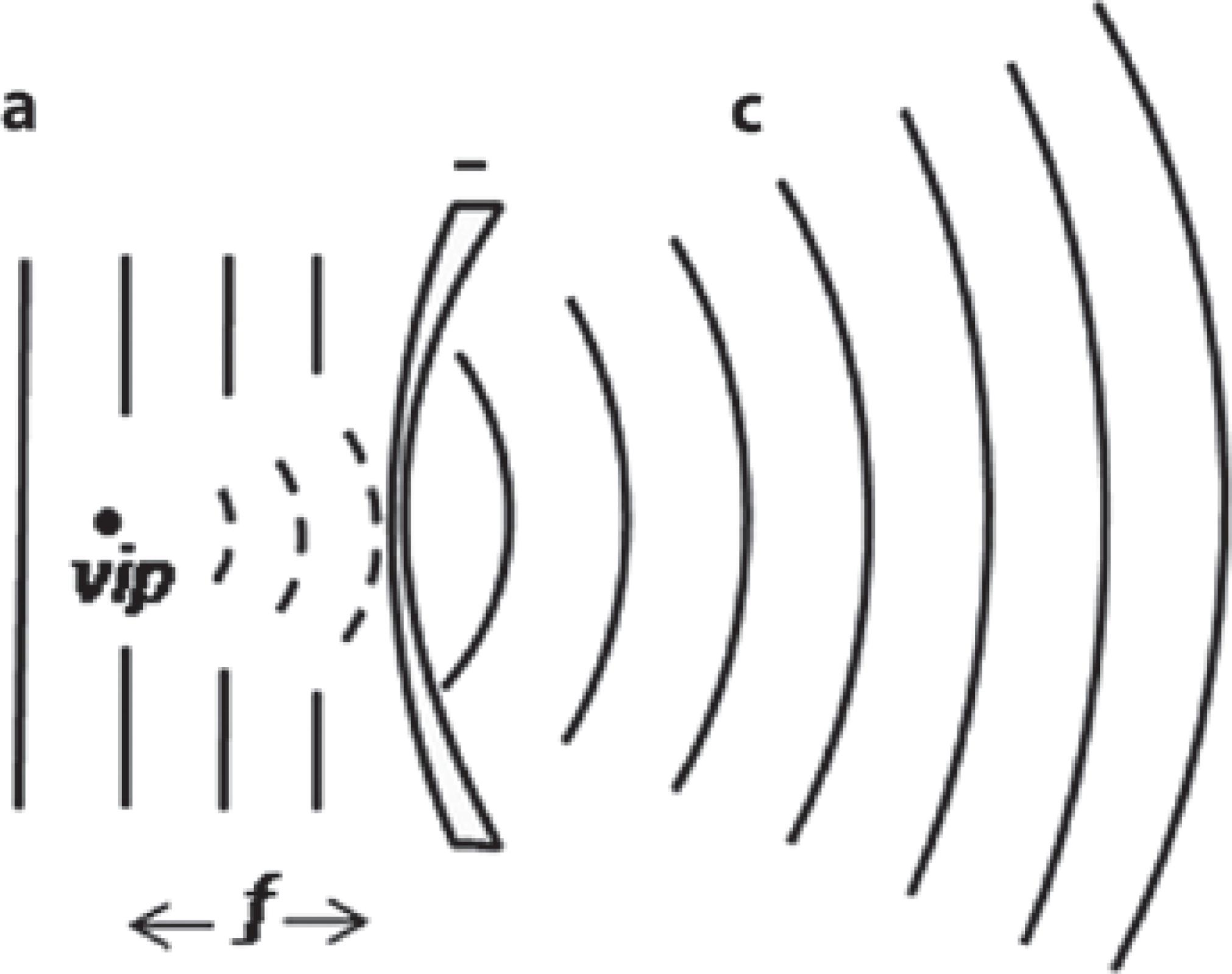
Figure 4 Backward projection of diverging waves in a concave lens. vip: virtual image point; ƒ: virtual focal distance. The image point is also the virtual focus of the lens, because the light comes from infinity; a and c are flat and convex wavefronts, respectively.
For the easy identification of the virtual sources of light, the following rule may be used: virtual objects are generated by light that strikes the lens with the concave (converging) wavefront configuration; virtual images are created by light that exits the lens with the convex (diverging) wavefront configuration.
Light rays
Light rays are imaginary lines that describe the path of light(26). They are helpful in finding the position, size, and orientation of images, even for complex optical systems. They are the basic tools of geometrical optics.
In an optically homogeneous medium, the rays are straight lines perpendicular to the wavefronts, which identify the direction of energy flow. When the wavefront is not at infinity, the light rays (being normal to a spherical surface) bend and intersect each other at the center of curvature of the sphere that defines its surface. In a sagittal plane containing the light source, these rays are arranged like the spokes of a wheel. If only one quadrant is considered, the rays configure an open fan whose apex is the light source (Figure 1B). When the wavefronts are flat, which is supposed to occur at infinity, the light rays form a bundle of parallel lines (Figure 1C). Thus, the enigma of the diverging rays that become parallel at infinity is due to the flattening of the wavefront. Because geometrical optics does not deal with wavefronts on a regular basis, it ends up causing this apparent enigma.
Another weakness of the bundle-of-rays approach is the difficulty it has in explaining vergence. The natural tendency is to represent a diverging bundle of rays as an open fan, with the vertex representing the object point and the rods representing the light rays (Figure 1B). So far, so good. The error occurs when one tries to guess the amount of vergence by the angle at the vertex of the fan. However, the angle is irrelevant here, since it is a distance-dependent variable. To find vergence (in a vacuum or in air) all that is needed is the reciprocal of the distance, in meters, from the wavefront to its source. Since geometrical optics does not work regularly with wavefronts, it does not convey vergence conveniently. Even authorities in visual optics occasionally neglect this fact(27).
Direction of the propagation of light
Regardless of the approach chosen to study the path of light, it is necessary to set up its direction of propagation. Once this is done, all distances are compared to it. There are different conventions for this goal(28-30) but the one we prefer is the following: light travels from left to right and distances are always measured from the curved surfaces (lens' or waves) to the light sources (object points, image points, the center of curvature). Distances opposing the direction of light are negative; distances agreeing with it are positive. Vertical distances are positive above the optical axis and negative below it. This is the Cartesian Sign Convention, in analogy to Cartesian graphs. It should always be remembered that the very form of the written optical equations depend on the convention adopted.
Final remarks
In visual optics, light rays and wave trains are complementary. The use of one or the other depends on what information you want to put into evidence. If the primary goal is the position, size, and orientation of the image, the first approach (light rays) is preferable. However, if the objective is to deal with the accommodative effort of the eye, or with the vergences of lenses or waves, an approach using wave trains will be more profitable.



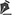
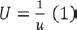
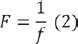
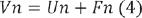
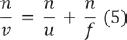
 English PDF
English PDF
 Print
Print
 Send this article by email
Send this article by email
 How to cite this article
How to cite this article
 Submit a comment
Submit a comment
 Mendeley
Mendeley
 Scielo
Scielo
 Pocket
Pocket
 Share on Linkedin
Share on Linkedin

