
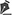
Luis Alberto Vieira de Carvalho1; Odemir Martinez Bruno1
DOI: 10.1590/S0004-27492005000600016
RESUMO
OBJETIVOS: A videoceratografia é tecnologia que vem sendo utilizada para análise da superfície da córnea desde meados dos anos 80. O objetivo deste trabalho é o desenvolvimento de diferentes técnicas para a detecção de bordas em imagens de Plácido e a comparação dos resultados obtidos em cada algoritmo, visando as conseqüências para o cálculo da curvatura axial. Métodos: Foram capturadas imagens de Plácido de 4 diferentes superfícies esféricas utilizando o equipamento Eyesys system 2000. Cada imagem foi salva no formato bitmap em disco rígido de um computador pessoal IBM PC. Seis algoritmos de processamento de imagem foram desenvolvidos utilizando técnicas documentadas na literatura. Os métodos considerados foram: (1) Derivada numérica de primeira ordem, (2) Derivada de Fourier de primeira ordem, (3) Derivada de Fourier de segunda ordem, (4) Filtro de Marr-Hildreth, (5) Filtro de Canny e (6) Laplaciano morfológico (morfologia matemática). Cada um dos algoritmos foi testado e analisado para imagens de Plácido. Resultados: As distâncias radiais do centro das imagens de Plácido às bordas obtidas por cada algoritmo foram comparadas com uma simulação computacional do sistema VK. A média do desvio padrão em pixels/milímetros/dioptria para todas as esferas para os métodos (1)-(6), respectivamente, foi: (1) 33,1695/0,7961/0,79, (2) 32,79/0,7870/0,7724, (3) 60,7150/1,4572/1,4192, (4)18,97/0,4553/0,4572, (5) 46,33/1,1119/1,0917, (6) 20,55/0,4932/0,48. Conclusão: Pesquisadores e oftalmologistas devem ficar atentos na escolha de equipamentos de videoceratografia e também quando comparar medidas de equipamentos diferentes, uma vez que podem ocorrer diferenças relacionadas ao método de processamento de imagens utilizado pelo fabricante. Demonstramos neste trabalho que o método de Marr-Hildreth é mais preciso que o método de Fourier ou métodos como derivada numérica.
Descritores: Topografia de córnea; Algoritmos; Córnea; Processamento de imagem assistida por computador
ABSTRACT
PURPOSE: Videokeratography (VK) has been a widespread technology for corneal surface analysis since the mid-80s. The objective of this study was to develop different techniques for Plácido image edge detection and compare the results of each algorithm in terms of the consequences for axial curvature computations. METHODS: Plácido images from an Eyesys system 2000 were captured for 4 different spherical surfaces.Each image was saved in bitmap format at the hard disk of an IBM computer. Six different image-processing algorithms were developed using different techniques well-documented in the literature. The six methods were as follows: (1) First order numerical derivative, (2) First and (3) Second order Fourier derivative, (4) the Marr-Hildreth filter, (5) Canny's Method, (6) Mathematical morphology. Each algorithm was tested on each of the Plácido images. RESULTS: Edge radial distance from center of Plácido image was compared for each algorithm and a computer simulation of the videokeratography system. Mean deviation in terms of pixels/millimeters/dioptric power for all spheres for methods (1)-(6) were, respectively: (1) 33.1695/0.7961/0.79, (2) 32.79/0.7870/0.7724, (3) 60.7150/1.4572/1.4192, (4)18.97/0.4553/0.4572, (5) 46.33/1.1119/1.0917, (6) 20.55/0.4932/0.48. CONCLUSION: Researchers and clinical ophthalmologists should be more careful when choosing commercial videokeratographs and also when comparing measurements of different instruments, given that there may be differences associated with the image processing technique. We have shown here that the Marr/Hildreth (method (4)) image processing method is more precise than other methods such as Fourier or first order numerical methods.
Keywords: Corneal topography; Algorithms; Cornea; Image processing computer-assisted
INTRODUÇÃO
Histórico
O interesse por modelos para descrição da superfície da córnea data mais de 150 anos(1). Nesta época já se sabia da importância da contribuição da córnea para o poder total de refração do olho. Embora os valores para a córnea, humor aquoso e os outros componentes do olho sejam bastante parecidos, é na interface ar-córnea que ocorre a maior refração dos raios de luz (aproximadamente 2/3 da refração total), devido à diferença do índice de refração entre estes meios. Usando a equação do fabricante de lentes(2):
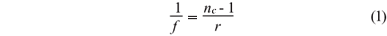
onde f é a distância focal em metros, ncé o índice de refração da córnea e r é o raio de curvatura em metros, podemos facilmente deduzir o poder refrativo da córnea.
Em 1880, o português A. Plácido desenvolveu um sistema para análise qualitativa da córnea cujo princípio é utilizado até os dias de hoje(3). O anteparo era uma cartolina preta com discos brancos concêntricos pintados na superfície. Havia um pequeno furo ao centro por onde o observador poderia analisar os reflexos da córnea do paciente. Quando o paciente fixava o olhar no centro dos discos o médico poderia observar a projeção dos discos na córnea, verificando os padrões (Figura 1A). Se o padrão da imagem virtual formada fosse o de discos aproximadamente circulares e concêntricos, a córnea poderia ser interpretada como aproximadamente esférica (Figura 1B); do contrário, a topografia seria de uma superfície distorcida (Figura 1C).
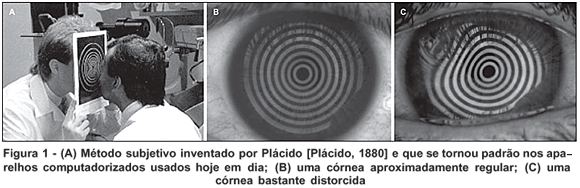
As repetidas tentativas no século passado de desenvolvimento de métodos quantitativos mais eficientes que permitissem medidas mais confortáveis para o paciente e mais práticas e objetivas para o oftalmologista deram origem a uma série de instrumentos computadorizados, hoje generalizados pelo nome de topógrafos de córnea (TC), cujo objetivo é calcular a distância entre os discos e por meio destes mapear a curvatura da córnea. O princípio óptico do TC pode ser visto na figura 2 e um instrumento comercial pode ser visto na figura 3.
Embora a videoceratografia hoje em dia seja uma técnica bem conhecida e difundida, não há referências claras na literatura ao método utilizado para processamento das imagens de Plácido. Isto ocorre provavelmente pela natureza comercial destes instrumentos, de tal maneira que os diferentes fabricantes procuram proteger suas tecnologias divulgando apenas resultados finais de suas técnicas e escrevendo patentes daquilo que consideram tecnologia inovadora.
No entanto, existe uma série de melhorias significativas nos algoritmos de processamento de imagens de Plácido que podem trazer benefícios para a comunidade de pesquisadores e usuários de TC. Além disso, há uma necessidade de formalização não somente dos métodos matemáticos para cálculo da curvatura, mas também de como os dados de interesse são extraídos das imagens de Plácido. Com estas informações podemos, por exemplo, analisar qual a influência da técnica de processamento de imagens na precisão dos valores de curvatura ou elevação da córnea, o que pode trazer melhorias importantes nos atuais métodos para cirurgia a laser da córnea(4-7).
É portanto, com base nestes argumentos, que implementamos neste trabalho diversas técnicas de processamento de imagens de Plácido, realizando a comparação quantitativa dos resultados obtidos e discutindo qual o melhor método para os atuais instrumentos. Este trabalho é importante, em termos práticos, para esclarecer ao médico oftalmologista, que esteja interessado em adquirir um videoceratógrafo, tanto para uso clínico como para pesquisas científicas, as diferenças na precisão dos mapas topográficos que podem surgir em função do método usado para processamento de imagens de Plácido. Salientamos que, em certos casos de córneas com superfícies sem grandes deformações, os resultados mostrados aqui podem não ser significativos, mas para córneas com maiores deformações, as diferenças podem ser bastante significativas. Na próxima seção apresentamos os métodos desenvolvidos.
MÉTODOS
Para testar os diferentes métodos de processamento de imagens de Plácido utilizamos dois métodos: medidas em esferas de calibração fabricadas em vidro, com raios de curvatura conhecidos, e uma simulação computacional dos discos de Plácido para as mesmas esferas. Desta maneira pudemos comparar os resultados dos algoritmos para superfícies cujos raios de curvatura são bem conhecidos e ao mesmo tempo sabe-se precisamente onde as bordas dos discos devem estar posicionadas, ou seja, os dados de controle são provindos da simulação computacional e os dados reais (medidos em esferas com raios conhecidos) são utilizados para se mensurar a precisão de nossos algoritmos.
Lendo o sinal da imagem de Plácido
Na seção anterior apresentamos o problema de processamento de imagens de Plácido de maneira qualitativa e informal. Com base no diagrama da figura 4 vamos formalizar o objetivo principal do algoritmo.
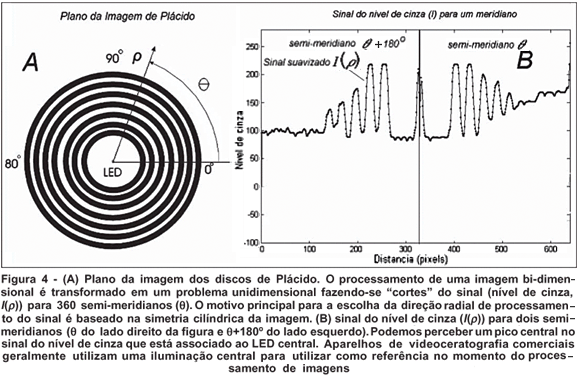
A detecção dos discos consiste basicamente em encontrar os pontos de borda de cada uma das transições entre discos claros e escuros na imagem de Plácido. Para isso torna-se imprescindível escolher um sistema de coordenadas convenientes, e este aspecto, como veremos mais adiante nesta seção, é também bastante importante para a precisão do algoritmo. Para as técnicas apresentadas neste trabalho escolhemos um sistema de coordenadas cilíndrico onde o nível de cinza é função das variáveis (r,q). O algoritmo encontra a posição do LED central e a partir deste ponto começa a detecção das bordas dos discos de Plácido. Outros autores descreveram métodos que examinam minuciosamente a imagem em linhas horizontais e determinam as bordas pela diferença na intensidade dos níveis de cinza(8). Nós sugerimos transformar a imagem de Plácido no plano cartesiano (x, y) para coordenadas polares (r,q), com a origem na posição da luz emitida por diodo- LED.
Isto simplifica o problema da detecção das bordas por causa da simetria aproximadamente polar dos discos. Examinando a imagem na direção radial (Figura 4A) esta tarefa pode ser reduzida para um problema unidimensional. Imprimindo-se a intensidade de nível de cinza 8 bits (0-preto até 255-branco) para ângulos polares entre 0 e 360 graus obtêm-se curvas com diferentes níveis de cinza (Figura 4B). Os níveis mais intensos estão associados aos discos mais brilhantes e os níveis de cinza menos intensos estão associados aos discos mais escuros da imagem.
A escolha de coordenadas polares para a varredura do sinal, contendo os níveis de cinza, não foi por acaso. O motivo disso está na simetria aproximadamente polar dos discos de Plácido. Caso as bordas fossem processadas em linhas verticais ou horizontais a direção de detecção não estaria alinhada com o gradiente dos níveis de cinza. Igarashi et al., realizou processamento em linhas horizontais e, embora argumente que obteve rapidez e precisão em seu algoritmo, utilizou modelos que na época não tinham precisão para detectar falhas no processamento de imagens(8). Neste trabalho comparamos 5 métodos para a detecção de bordas. São eles: (1) derivada numérica, (2) 1ª e 2ª derivadas de Fourier, (3) detector de borda Marr-Hildreth(9), (4) Algoritmo de Canny(10) e (5) Laplaciano morfológico. Todos estes métodos serão discutidos em maiores detalhes nas subseções seguintes.
Extração de bordas usando a primeira derivada do sinal
(a) Derivada numérica
Um grande número de filtros digitais para a detecção de bordas são inspirados em métodos derivativos de primeira ordem (ex.: Sobel, Roberts, entre outros)(11), que consistem basicamente em realizar uma operação de derivação na imagem, onde máximos e mínimos locais correspondem às bordas. Estes métodos, entretanto, são tradicionalmente aplicados em imagens planas, ou seja, bidimensionais e embora consigam detectar os discos de Plácidos, não apresentam um resultado satisfatório, conforme discutimos na seção (1). Uma vez que a imagem foi convertida para o sistema de coordenada polar e o sinal é processado individualmente para cada ângulo, estaremos tratando com sinais unidimensionais, definidos como I(r). Deste modo, neste trabalho diversos métodos tradicionais para detecção de bordas encontrados na literatura com bidimensionais serão adaptados para unidimensionais. O método da derivada numérica, consiste basicamente em suavizar I(r), com um filtro espacial mediano(11) e aplicar a derivada numérica no sinal.
(b) Derivada de Fourier
Outra maneira de obter a derivada de uma função discreta é através da propriedade derivativa da transformada de Fourier. Originalmente proposta por Papas(5) esta interessante propriedade permite calcular a derivada e a integral de uma função, através de operações em pares de Fourier, conforme descrevemos a seguir: Sejam q(t) « Q(f) pares de Fourier no domínio do tempo e da freqüência respectivamente e k um real não negativo, que define a ordem da derivação, a propriedade derivativa de Fourier é definida por:
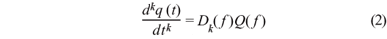
onde
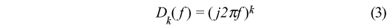
Utilizamos este princípio para obter a I'(r) e para reduzirmos o ruído do sinal, acrescentamos na equação o termo Gs (f), obtendo a equação (4).
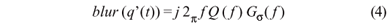
Filtro de Marr-Hildreth
O filtro de Marr-Hildreth é um dos detectores de borda mais populares em processamento de imagens. Uma das razões para tanto é a sua forte base biológica, um vez que foram localizados campos receptivos na retina que apresentam características semelhantes(9). O método é baseado na segunda derivada da gaussiana:
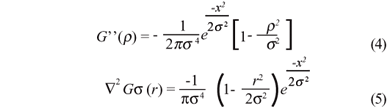
onde r = x2 + y2.
O filtro de Marr-Hildreth pode ser adaptado facilmente para uma variável, sendo visto como a segunda derivada da gaussiana (equação 6). Para determinar as bordas do sinal I(r), é realizada a convolução com o filtro de Marr-Hildreth unidimensionais e localizados os cruzamentos no eixo x (cruzamentos por zero), que correspondem as bordas do sinal.
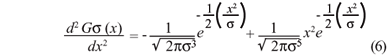
Método de Canny
O método de Canny para detecção de bordas foi introduzido em 1986(5), como uma proposta para a obtenção de um filtro ideal em processamento de sinais. Basicamente o método de Canny é fundamentado na primeira derivada da gaussiana:
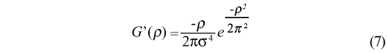
Este método também foi originalmente proposto para aplicações em imagens. Seu algoritmo consiste no processamento dos sinais compostos pelas linhas e colunas da imagem convoluindos com Gaussianas unidimensionais e suas derivadas nos eixos x e y, apresentando todas as curvas o mesmo s. Deste modo, o método, extrai as bordas dos sinais unidimensionais das colunas e das linhas da imagem individualmente e posteriormente realiza a composição do resultado.
O algoritmo de Canny pode ser resumido como:
Passo 1
A imagem original (representada por Img) é suavizada fazendo-se uma convolução com uma função Gaussiana unidimensional em cada direção, o que pode ser representado pelas equações:
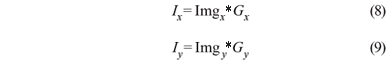
Passo 2
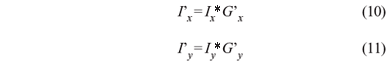
Passo 3
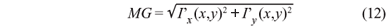
onde MG é o mapa de gradientes resultante do algoritmo. As bordas são definidas como os máximos locais de MG.
Como neste trabalho os sinais são coordenadas polares definidas como I(r,q), o filtro de Canny é aplicado apenas ao eixo r. Deste modo para cada q iremos aplicar o processamento ao sinal I(r) correspondente. Desta forma, uma adaptação do método de Canny para o processamento unidimensional dos discos pode ser resumida nos seguintes passos:
Passo 1
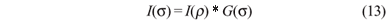
Passo 2
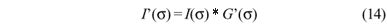
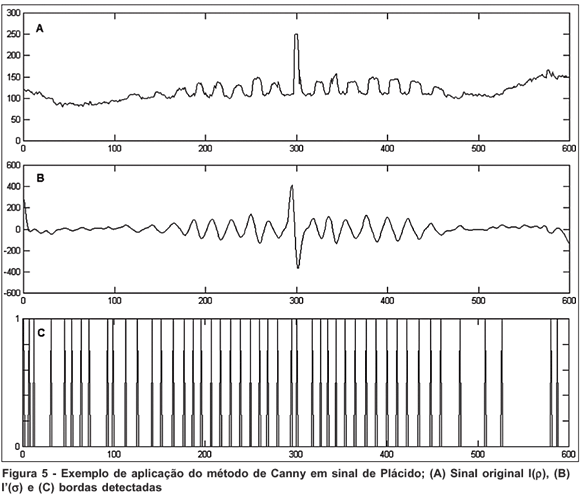
Uma vez que os gradientes estão orientados no eixo r, I's é o mapa de gradientes do processo. As bordas do sinal equivalem aos picos do módulo do mapa de gradiente. A figura 5 ilustra o método, onde em (A) é apresentado o sinal I(r), em (B) temos a derivada I'(s) correspondente e em (C) os picos (positivos e negativos) de I'(s), que correspondem às bordas do sinal.
Morfologia matemática
Laplaciano através de morfologia matemática
A morfologia matemática é uma técnica de análise de imagem que se desenvolveu a partir dos anos sessenta. Inicialmente seu domínio de aplicação incluía imagens microscópicas, mas com a evolução dos métodos, seu domínio se estendeu para as demais áreas de aplicações de processamento de imagens. Em morfologia matemática, os pixels na imagem, ao invés de serem considerados como sinais, são tratados como elementos de conjuntos. O seu princípio básico consiste em processar as informações relativas à geometria e à topologia de um conjunto de elementos, utilizando transformações de formas, realizados através de operadores elementares conhecidos como erosão e dilatação. Embora inicialmente a morfologia matemática fosse aplicada apenas a imagens binárias, suas técnicas foram adaptadas e estendidas para imagens de tons de cinza e até mesmo cromáticas. A técnica apresentada aqui é obtida através da morfologia matemática de tons de cinza.
Uma das formas de detectar bordas através de morfologia matemática é através do método conhecido como operador Laplaciano morfológico. Sejam as operações morfológicas de dilatação e erosão em níveis de cinza definidas respectivamente como:
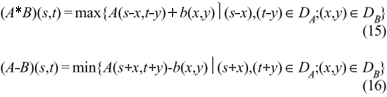
O operador Laplaciano morfológico é dado por:
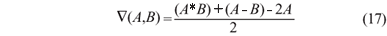
Onde B é um elemento estruturante e centralizado. Embora o operador Laplaciano morfológico seja aplicado a imagens, basta definir o conjunto A e B como elementos de um vetor para sua adaptação unidimensionais. Similar ao processo de detecção de bordas do filtro de Marr-Hildreth (subseção 2.3) as bordas no Laplaciano morfológico são obtidas através de cruzamentos por zero.
RESULTADOS
Para comparar o resultado entre os métodos, quando aplicados ao grupo de controle, foi implementada uma simulação computacional do funcionamento do videoceratógrafo (Figura 6).
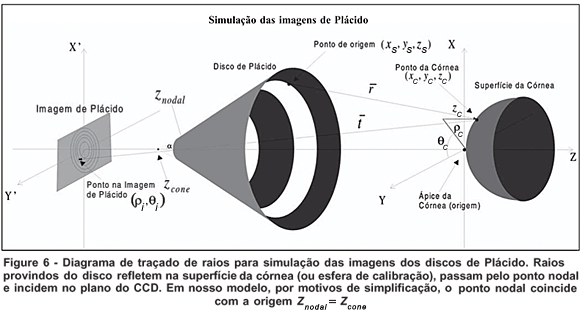
Os pontos de borda dos discos de Plácido (xs,ys,zs) são traçados até a superfície da córnea (ou da esfera) (xc,y c,zc) e depois de refletidos passam pelo ponto nodal (Zcone)sobre o eixo óptico (Z). A intersecção deste segmento com o plano da imagem (CCD) utilizando o princípio de Fermat (minimização do caminho óptico 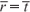 ) nos fornece as coordenadas para a imagem de Plácido simulada (para maiores detalhes de implementação de tal simulação veja referência(12). Estas simulações foram efetuadas para 4 superfícies esféricas de raios 7,73 mm, 8,05 mm, 8,34 mm e 8,96 mm, pois estes são os raios das esferas reais que utilizamos para gerar as imagens de Plácido.
) nos fornece as coordenadas para a imagem de Plácido simulada (para maiores detalhes de implementação de tal simulação veja referência(12). Estas simulações foram efetuadas para 4 superfícies esféricas de raios 7,73 mm, 8,05 mm, 8,34 mm e 8,96 mm, pois estes são os raios das esferas reais que utilizamos para gerar as imagens de Plácido.
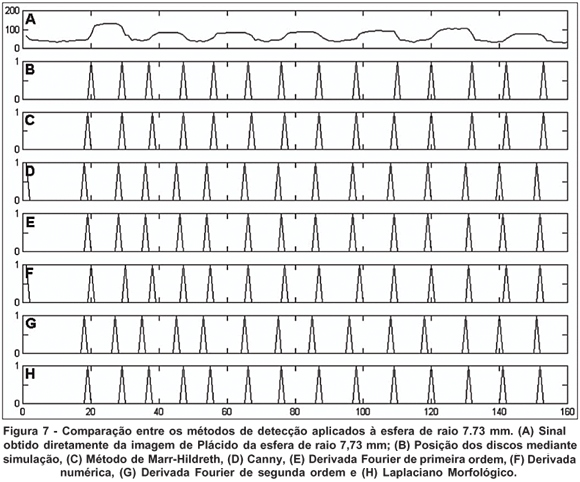
Deste modo pudemos comparar os resultados dos pontos de borda obtidos com cada um dos métodos mostrados na seção (2) aplicados às superfícies de controle com dados teóricos obtidos na simulação. Na figura 7 é apresentado um exemplo que ilustra esta comparação. O primeiro gráfico desta figura (A) apresenta o sinal I(r), extraído do meridiano 45º da esfera de raio 7,73 mm; o gráfico (B) apresenta a posição das bordas dos discos segundo a simulação teórica (sem erros); os demais gráficos apresentam a posição das bordas, aplicada a I(r), para cada uma das técnicas de detecção discutidas neste artigo. Como podemos observar, existem divergências entre as posições dos discos nos gráficos, indicando diferenças entre os resultados dos métodos de detecção de bordas. Observe que estas diferenças ocorrem tanto entre cada um dos métodos como também quando comparados com o resultado da simulação teórica.
Para quantificar o desvio calculamos o erro quadrático médio para cada um dos métodos e cada uma das superfícies esféricas em termos da distância radial (r) para cada disco usando:
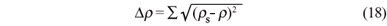
onde rs é a distância teórica obtida na simulação e r é a distância calculada usando cada um dos métodos propostos. Estes dados podem ser vistos na tabela 1.
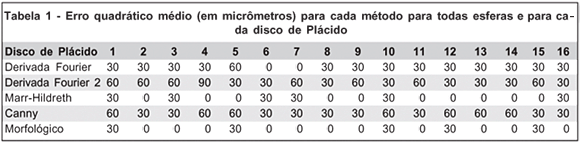
A média dos erros para todos os discos e para cada esfera também foi calculada e pode ser vista na tabela 2.
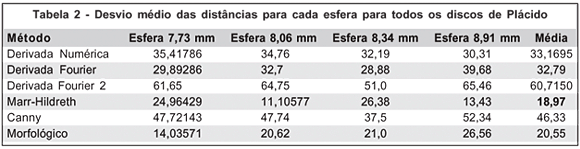
Além disso, fizemos comparações entre os métodos em termos dos resultados finais apresentados em VC, ou seja, o poder dióptrico. Estes instrumentos normalmente apresentam os resultados na forma de curvaturas (inverso do raio de curvatura), mais especificamente na forma de poder dióptrico, que é proporcional à curvatura e dado pela equação (1). Em termos de conseqüências para a videoceratografia foi aplicado o seguinte método de avaliação: os valores das posições de borda utilizando cada um dos métodos foi inserida em um algoritmo conhecido para cálculo da curvatura axial(13-14). A média dos 5760 valores de dioptria foi calculada para cada esfera (como se tratam de esferas deveríamos teoricamente ter valores próximos para cada esfera, já que têm curvaturas aproximadamente constantes). Ou seja, raios de curvatura e poder dióptrico foram calculados para todas as superfícies baseados na detecção das bordas proveniente de cada método e também para as bordas provenientes da simulação teórica. Os resultados para o desvio quadrático médio (em Dioptrias) podem ser vistos na tabela 3.
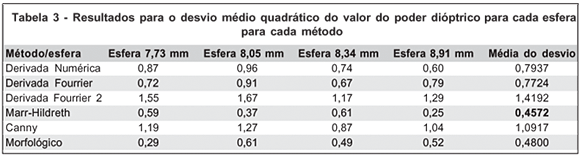
CONCLUSÃO
Implementamos neste trabalho uma série de algoritmos baseados em diferentes técnicas de processamento de imagens para detecção de bordas de imagens de Plácido para esferas de diferentes diâmetros. O objetivo principal foi demonstrar a importância e ao mesmo tempo as conseqüências diretas no resultado final de um instrumento oftalmológico largamente utilizados em clínicas e hospitais - o videoceratógrafo. Como estes instrumentos são utilizados para avaliação da principal superfície refrativa do olho (a córnea), medidas mais precisas podem ter conseqüências diretas na precisão do diagnóstico ou intervenção cirúrgica do oftalmologista.
Como podemos perceber pelos resultados apresentados nas tabelas 2 e 3, o método mais preciso para detecção dos discos de Plácido, e portanto para cálculo do poder dióptrico axial da córnea, é aquele de Marr-Hildret. O Laplaciano morfológico é o segundo método mais preciso. Estes dois métodos são similares, uma vez que se baseiam no laplaciano da gaussiana, diferenciando-se apenas na metodologia e teoria de aplicação. Podemos afirmar isso pois o filtro de Marr-Hildreth é originário de processamento de sinais e análise de Fourier enquanto que o Laplaciano morfológico utiliza os conceitos de morfologia matemática inspirados na teoria dos conjuntos, geometria diferencial e topologia. Devemos lembrar que os resultados obtidos neste trabalho são conclusivos apenas com relação ao processamento de imagens dos discos de Plácido para videoceratografia. Geralmente em processamento de imagens não existe uma solução conclusiva para todos os problemas com apenas um método. Na maioria dos casos são necessários diferentes métodos para cada problema específico.
As descobertas realizadas neste trabalho são importantes tanto para pesquisadores e fabricantes de videoceratógrafos assim como para o médico oftalmologista. Isto reside no fato de que os resultados mostram as conseqüências diretas e quantitativas dos erros nos mapas dióptricos da córnea associados aos erros na detecção dos discos de Plácido. Até onde sabemos estes resultados são inéditos e isso se deve provavelmente à não divulgação dos métodos utilizados por cada fabricante. No entanto, acreditamos que os resultados apresentados aqui possam estimular a divulgação e melhoria destes algoritmos.
A aplicação de métodos mais precisos para cálculo das imagens de Plácido é algo que deve ser perseguido por todos aqueles que trabalham com pesquisas ou que utilizam diretamente os videoceratógrafos. O aumento de precisão é algo que beneficia a todos e estimula o aprimoramento de algoritmos para cálculo de outros parâmetros associados à córnea, como a elevação, curvaturas tangenciais (ou instantâneas, diferentes das curvaturas axiais calculadas aqui), entre outros.
REFERÊNCIAS
1. Schanzlin DJ, Robin JB. Corneal topography-measuring and modifying the cornea. New York: Springer-Verlag; 1991.
2. Born M, Wolf E. Principles of optics. 6 ed. New York: Pergamon; 1975.
3. Plácido A. Novo instrumento de exploração da córnea. Periódico d'Oftalmológica Practica (Lisboa). 1880;5:27-30.
4. Nakano K, Portellinha W, Oliveira M, Alvarenga L, Nakano C, Nakano E. Refractive outcome of Nidek OPD-scan customized ablations, J Refract Surg. 2003;19(2 Suppl):S221-2.
5. Papas TN. An adaptive clustering algorithm for image segmentation. IEEE Trans Signal Processing. 1992; 40:901-14.
6. Phusitphoykai N, Tungsiripat T, Siriboonkoom J, Vongthongsri A. Comparison of conventional versus wavefront-guided laser in situ keratomileusis in the same patient. J Refract Surg. 2003;19(2 Suppl):S217-20.
7. Vinciguerra P, Camesasca FI, Urso R. Reduction of spherical aberration with the nidek NAVEX customized ablation system, J Refract Surg. 2003;19(2 Suppl): S195-201.
8. Igarashi H, Kojima M, Igarashi S, Yoshida A, Cheng HM.A simple and effective videokeratometric system, Acta Ophthalmol Scand. 1995;73(4):336-9.
9. Parker JR. Algorithms for image processing and computer vision. New York: John Wiley & Sons; 1996.
9. Marr D. Vision: a computational investigation into the human representation and processing of visual information. San Francisco: W. H. Freeman; 1982.
10. Canny J. A computational approach to edge detection, PAMI- 5. IEEE Trans Patt Anal Machine Intell. 1986;8(6):679-98.
11. Gonzales RC, Woods RE. Digital image processing. New York: Addison-Wesley; 1992.
12. Klein SA. Corneal topography reconstruction algorithm that avoids the skew ray ambiguity and the skew ray error. Optom Vis Sci. 1997;74(11):945-62.
13. Carvalho LA, Tonissi SA, Romão AC, Santos LE, Yasuoka F, Oliveira AC, et al. Desenvolvimento de um instrumento computadorizado para medida do poder refrativo da córnea (Videoceratógrafo). Arq Bras Oftalmol. 1998;61(6):640-54.
14. Carvalho LA, Tonissi SA, Castro JC. Preliminary results of a computerized Plácido disc surgical corneal topographer. In: 9º SPIE Conference on Ophthalmic Technologies, San Jose, California, January 1999. p.53-62.
Endereço para correspondência
University of Rochester
Meliora Hall 242 - Rochester, NY 14627
E-mail: [email protected] ou [email protected] ou [email protected]
Recebido para publicação em 30.03.2005
Versão revisada recebida em 28.09.2005
Aprovação em 20.10.2005
Apoio financeiro: FAPESP, processo #03132-8
Nota Editorial: Depois de concluída a análise do artigo sob sigilo editorial e com a anuência da Dra. Belquiz Rodrigues do Amaral Nassaralla sobre a divulgação de seu nome como revisora, agradecemos sua participação neste processo.