RESUMO

OBJETIVO: Avaliar a utilidade da análise de Fourier como método para detecção de defeitos localizados na camada de fibras nervosas da retina (CFN), utilizando as medidas obtidas com a polarimetria de varredura a laser. MÉTODOS: O estudo incluiu 40 olhos de 40 pacientes com glaucoma apresentando defeitos localizados na CFN detectados à oftalmoscopia e/ou em fotografias da camada de fibras nervosas. O grupo controle foi constituído por 43 olhos de 43 pacientes normais, sem antecedente de pressão intra-ocular elevada ou glaucoma, e com exame normal da CFN e disco óptico. Todos os pacientes foram submetidos a exame da CFN utilizando o aparelho GDx® - Nerve Fiber Analyzer. Para comparação entre os grupos, foram utilizados os parâmetros fornecidos pelo software do aparelho e medidas provenientes dos coeficientes obtidos pela análise de Fourier da curva de distribuição dos valores de espessura da CFN. As várias medidas dos coeficientes de Fourier foram combinadas numa função linear discriminante de maneira a encontrar a combinação que resultasse na melhor separação entre pacientes glaucomatosos com defeitos localizados e os sujeitos normais. Curvas ROC foram construídas para cada medida e valores de sensibilidade para especificidades fixas foram calculados. RESULTADOS: Os parâmetros fornecidos pelo software do GDx mostraram baixo poder de diferenciação entre os pacientes normais e com defeitos localizados na CFN, com sensibilidades variando de 15 a 48% (com especificidade a 91%). Para a mesma especificidade de 91%, a combinação dos coeficientes de Fourier teve sensibilidade de 80%. A área sob a curva ROC para a combinação dos coeficientes de Fourier (0,90) foi significativamente superior à obtida para o parâmetro The Number (0,76). CONCLUSÃO: A análise de Fourier resultou em melhora na capacidade do GDx de detectar defeitos localizados na CFN em relação aos parâmetros fornecidos pelo software do aparelho.

Descritores: Análise de Fourier; Glaucoma; Fibras nervosas; Retina; Técnicas de diagnóstico oftalmológico

ABSTRACT

PURPOSE: In this study, we performed Fourier analysis of retinal nerve fiber layer (RNFL) thickness measurements obtained with scanning laser polarimetry and evaluated the ability of this method to detect localized nerve fiber layer defects in glaucomatous patients. METHODS: The study included 40 eyes of 40 glaucomatous patients with localized RNFL defects identified by slit-lamp biomicroscopy or RNFL photography and 43 eyes of 43 normal patients. The patients were submitted to RNFL thickness measurements using the GDx® - Nerve Fiber Analyzer. Fourier analysis was applied to the polarimetry data. Fourier coefficients and GDx parameters were compared between the two groups. A linear discriminant function was developed to identify and combine the most useful Fourier coefficients to separate the two groups. ROC curves were obtained for each measurement and sensitivity values (at fixed specificities) were calculated. RESULTS: The combination of Fourier coefficients resulted in a sensitivity of 80% for a specificity set at higher than 90%. For the same specificity, the GDx parameters had sensitivities ranging from 15% to 48%. The area under the ROC curve (AUC) for the combination of Fourier coefficients was 0.90, significantly higher than the AUC for the parameter The Number (0.76). CONCLUSION: Fourier analysis of RNFL polarimetry data had a better diagnostic performance than standard GDx parameters to identify localized retinal nerve fiber layer defects in glaucomatous patients.

Keywords: Fourier analysis; Glaucoma; Nerve fibers; Retina; Diagnostic techniques, ophthalmological

---

 

 

INTRODUÇÃO

Nos últimos vinte anos, a avaliação minuciosa da camada de fibras nervosas da retina (CFN) se tornou uma ferramenta fundamental para o diagnóstico do glaucoma. Defeitos na CFN podem preceder em vários anos as alterações de campo visual e sua identificação pode auxiliar na detecção precoce da doença⁽¹⁾.

As alterações glaucomatosas na camada de fibras nervosas podem ser classificadas como difusas, localizadas, ou mistas⁽²⁾. À oftalmoscopia, a atrofia difusa da CFN mostra-se como uma diminuição generalizada do brilho e estriações característicos das fibras nervosas, associada a uma melhor visualização dos vasos sanguíneos retinianos. Os defeitos localizados, por sua vez, aparecem como uma faixa escura, em forma de cunha, se alargando a partir do nervo óptico, o que tem sido referido em nosso meio como sinal de Hoyt^(3-5). Os defeitos localizados praticamente inexistem em indivíduos normais, isto faz com que sejam um marcador muito específico da presença de doença, sendo então fundamental sua detecção⁽⁶⁾.

Os métodos qualitativos ou semiquantitativos de observação da CFN, como oftalmoscopia e fotografias, apresentam alguns inconvenientes. Além da avaliação ser subjetiva, e depender grandemente da experiência do examinador, a visibilidade da CFN depende da quantidade de melanina presente no epitélio pigmentado da retina do paciente e normalmente necessita transparência ótima dos meios e dilatação pupilar máxima^(7-8). Além disso, até 50% das fibras nervosas podem ser perdidas sem que seja possível detectar alteração na CFN por meio de fotografias⁽⁹⁾.

O analisador da camada de fibras nervosas – GDx^® Nerve Fiber Analyzer (Laser Diagnostic Technologies, Inc., San Diego, CA, Estados Unidos) é um polarímetro de varredura a laser designado para medir, de maneira objetiva e quantitativa, a espessura da camada de fibras nervosas da retina in vivo^(10-14). O GDx tem se mostrado promissor na diferenciação entre pacientes normais e glaucomatosos, com boa reprodutibilidade entre os exames^(15-26). Além disso, a obtenção de imagens com esse aparelho não requer dilatação pupilar^(22-23).

Nos indivíduos normais, os valores de espessura da CFN em torno do disco óptico, obtidos com o GDx, formam um padrão característico, com uma distribuição bimodal, conhecido como curva em dupla corcova (double-hump curve)^(27-28). A perda de fibras nervosas no glaucoma leva a alterações nesta curva, seja pela redução de sua amplitude ou por mudanças na sua forma⁽¹⁵⁾. É sabido que a espessura da CFN varia amplamente entre os indivíduos normais, fato que limita a utilização dos valores absolutos de espessura da CFN para separar pacientes glaucomatosos de indivíduos normais⁽¹⁵⁾. A análise da forma global da curva de distribuição dos valores de espessura da CFN, enfatizando diferenças relativas entre porções da curva, poderia então ser mais útil para separar os dois grupos. O estudo desta curva pode ser realizado através de um procedimento matemático denominado análise de Fourier^(29-30).

A análise de Fourier consiste na decomposição de uma determinada onda ou curva em seus componentes sinusoidais, cada um com sua freqüência. Este método fornece a amplitude e fase dos diversos componentes sinusoidais que, quando somados, restituem a onda original^(30-32). Ondas complexas podem então ser decompostas em vários componentes, cuja análise fornece uma maneira de se estudar a onda original. Desta forma, a aplicação da análise de Fourier na curva de distribuição dos valores de espessura da CFN fornece uma maneira de estudarmos melhor esta curva, enfatizando alterações na sua forma. Ao enfatizar as diferenças relativas entre os vários setores, este método poderia ser superior às medidas de espessura absoluta da CFN para detecção de defeitos localizados na camada de fibras nervosas da retina.

Neste estudo, nós aplicamos a análise de Fourier como método para avaliação das medidas de espessura da CFN obtidas com o GDx e avaliamos sua habilidade em detectar defeitos localizados da camada de fibras nervosas da retina em pacientes com glaucoma.

 

MÉTODOS

O presente estudo incluiu pacientes normais e pacientes com glaucoma apresentando defeitos localizados da camada de fibras nervosas da retina. Todos os pacientes foram avaliados no Serviço de Glaucoma do Hospital das Clínicas da Faculdade de Medicina da Universidade de São Paulo, tendo fornecido consentimento voluntário para o estudo. O estudo seguiu os princípios regidos na Declaração de Helsinque. Todos os indivíduos foram submetidos a exame oftalmológico consistindo de medida da acuidade visual corrigida, biomicroscopia, medida da pressão intra-ocular, gonioscopia e oftalmoscopia com pupilas dilatadas. Além disso, todos os pacientes realizaram exame de campo visual com o perímetro Humphrey (estratégia Full-Threshold 30-2 ou 24-2) e exame da camada de fibras nervosas com o aparelho GDx. O intervalo entre os exames foi de no máximo seis meses.

Indivíduos normais não apresentavam história de doença oftalmológica ou neurológica, nem antecedente familiar de pressão intra-ocular elevada ou glaucoma. Ao exame oftalmológico, apresentavam AV corrigida melhor ou igual a 20/40; erro refracional menor ou igual a 5,00DE ou 2,50DC; PIO menor ou igual a 21mmHg; ângulo da câmara anterior aberto, nervo óptico e camada de fibras nervosas de aspecto normal.

Pacientes com glaucoma não apresentavam antecedentes de doença neurológica ou cirurgia intra-ocular prévia. Ao exame oftalmológico, apresentavam AV corrigida melhor ou igual a 20/40; erro refracional menor ou igual a 5,00DE ou 2,50DC e ângulo da câmara anterior aberto. Para inclusão no estudo, os pacientes com glaucoma deveriam apresentar defeitos localizados típicos da camada de fibras nervosas da retina, detectados pelo exame biomicroscópico com lente de Volk (78D); ou por meio de fotografias da camada de fibras nervosas com red-free, segundo método previamente descrito^(6,8). A pressão intra-ocular não foi utilizada como critério para inclusão ou exclusão do estudo nos pacientes com glaucoma. Caso os dois olhos de um mesmo paciente satisfizessem os critérios de inclusão, apenas um olho era randomicamente selecionado para inclusão no estudo.

Todos os indivíduos foram submetidos a exame da camada de fibras nervosas utilizando um polarímetro de varredura a laser - o aparelho GDx – Nerve Fiber Analyzer (Laser Diagnostic Technologies, Inc., San Diego, CA, Estados Unidos). Os princípios de funcionamento deste aparelho estão descritos em detalhe na literatura^(15-16). Em suma, a medida de espessura da camada de fibras nervosas empregando a polarimetria a laser baseia-se nas propriedades birrefringentes da camada de fibras nervosas da retina^(10-14). Quando uma luz polarizada incide sobre um meio birrefringente, ela sofre um retardo que é linearmente relacionado à espessura e propriedades ópticas deste meio. O software do aparelho então converte as medidas de retardo da CFN em micrômetros de espessura de acordo com escala previamente estabelecida.

Para cada paciente foram obtidas seis imagens de cada olho, sendo que as três melhores foram utilizadas para compor uma imagem média. O desvio-padrão (DP) da imagem média foi de 8mm ou menor para inclusão. De cada imagem média, uma elipse demarcando as bordas do disco óptico foi desenhada, e uma elipse de 10 pixels de espessura, concêntrica a margem do disco óptico e a 1,7 diâmetros discais deste foi automaticamente determinada pelo aparelho. Esta elipse foi dividida em 16 setores iguais (cada um compreendendo 22,5°) de acordo com o software do aparelho. A espessura da CFN num determinado setor representa a média dos valores de espessura de cada pixel deste setor. Assim, para cada olho, obtivemos 16 medidas de espessura, sendo 8 relativas a hemiretina superior e 8 relativas a hemiretina inferior.

Análise dos dados

A análise de Fourier é um procedimento matemático no qual uma onda ou curva complexa pode ser decomposta em um conjunto de ondas sinusoidais harmônicas de freqüências, amplitudes e fases específicas⁽³⁰⁾. Quando adicionadas ponto a ponto, estes componentes reproduzem o padrão original. O componente de menor freqüência é chamado de fundamental, e corresponde a forma básica da curva original. Os outros componentes têm freqüências que são múltiplos inteiros da freqüência do componente fundamental. Assim, os componentes de maior freqüência servem para moldar o fundamental de maneira que a composição de todos eles se aproxima da curva original. A transformada rápida de Fourier (FFT – Fast Fourier Transform) é um algoritmo matemático utilizado para a obtenção dos coeficientes (isto é, suas amplitudes e fases) dos diversos componentes sinusoidais^(31-32). O programa Mathematica v.4 (Wolfram Research, Inc., Champaign, IL, Estados Unidos) foi utilizado para realização do algoritmo FFT. Quando aplicado a um conjunto de 8 pontos representando a curva de espessura de uma hemiretina, o FFT resulta em 5 coeficientes – o chamado DC (medida escalar, análoga a média geral), o fundamental, o segundo harmônico, o terceiro harmônico e o quarto harmônico. Os coeficientes representam as contribuições relativas de cada componente para moldar a curva original.

Neste estudo, a análise de Fourier dos valores de espessura da CFN fornecidos pelo GDx foi realizada de maneira similar à anteriormente descrita na literatura⁽³³⁾. Várias medidas foram obtidas a partir dos coeficientes de Fourier fornecidos: F_fun (coeficiente do componente fundamental), F_soma (somatório dos coeficientes do fundamental, segundo, terceiro e quarto harmônicos), F_assimfun (quociente entre o F_fun superior e o F_fun inferior, representando a assimetria existente entre as duas hemiretinas no componente fundamental) e F_assimsoma (quociente entre o F_soma superior e o F_soma inferior, representando a assimetria do somatório de todos os coeficientes entre as duas hemiretinas). As várias medidas dos coeficientes de Fourier foram combinadas numa função linear discriminante de maneira a encontrar a combinação que resultasse na melhor separação entre pacientes glaucomatosos com defeitos localizados e os sujeitos normais.

Curvas ROC (Receiver Operating Characteristic) foram obtidas para cada medida e valores de sensibilidade e especificidade e pontos de corte associados foram calculados. Como método de validação interna da função discriminante e estimativa do viés, utilizamos o procedimento de reamostragem "bootstrap". Em essência, este método consiste em obter B (B=1000, neste estudo) amostras aleatórias, com reposição, da amostra original. O modelo é estimado em cada amostra "bootstrap" e avaliado na amostra original e na amostra "bootstrap". A média da diferença entre essas performances nas 1000 replicações é uma estimativa do "otimismo" na performance aparente. Este método tem sido apontado como o melhor para validação interna de modelos preditivos⁽³⁴⁾.

Além das análises descritas acima, também calculamos o poder diagnóstico de vários dos parâmetros de espessura da CFN fornecidos pelo software do GDx. Os parâmetros utilizados em nosso estudo foram: The Number, Symmetry, Superior Ratio, Inferior Ratio, Superior/Nasal, Max Modulation, Ellipse Modulation, Average Thickness, Ellipse Average, Superior Average, Inferior Average e Superior Integral. As definições destes parâmetros foram publicadas previamente⁽¹⁶⁾. Curvas ROC foram obtidas para cada um dos parâmetros citados e valores de sensibilidade foram calculados para especificidades fixas.

As comparações dos diversos parâmetros e coeficientes de Fourier entre os olhos normais e glaucomatosos foram realizadas utilizando-se teste t de Student com correção de Bonferroni para múltiplas comparações (a=0,002; 24 comparações). Diferenças nas áreas sob as curvas ROC foram calculadas segundo método previamente descrito⁽³⁵⁾. As análises estatísticas foram realizadas utilizando o programa SPSS for Windows v.10.0 (SPSS Inc., Chicago, IL, Estados Unidos) e S-Plus 2000 (MathSoft, Inc., Seattle WA, Estados Unidos).

 

RESULTADOS

Foram incluídos no estudo 43 pacientes normais com média de idade (± DP) de 45 ± 11 anos, e 40 pacientes glaucomatosos com defeitos localizados na CFN com média de idade de 58 ± 12 anos (p<0,01). Dos 40 pacientes com glaucoma, 31 (77%) apresentavam defeitos localizados na CFN inferior, 6 (15%) defeitos na CFN superior, e 3 (8%) defeitos em ambas as regiões. As médias do MD e CPSD dos exames de campo visual dos pacientes glaucomatosos foram -5,62 ± 3,64dB e 6,76 ± 3,94dB, respectivamente.

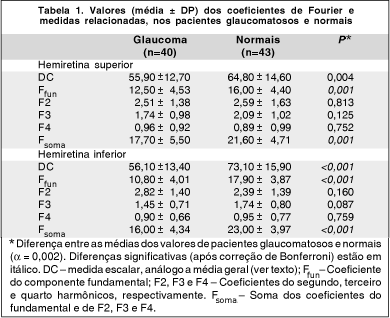
Na tabela 1 estão sumarizados os valores dos coeficientes de Fourier dos pacientes normais e glaucomatosos. A amplitude do componente fundamental foi significativamente menor nos pacientes com glaucoma que nos indivíduos normais, tanto para a hemiretina superior quanto para a inferior. Quanto às amplitudes do segundo, terceiro e quarto harmônicos, não foram observadas diferenças significativas entre os grupos, após correção de Bonferroni. Para avaliar a habilidade dos diversos componentes de Fourier em separar os pacientes glaucomatosos dos normais, utilizamos o menor valor de F_fun (minF_fun) e F_soma (minF_soma) entre as duas hemiretinas, para cada um dos 83 olhos. A combinação de minF_fun, minF_soma e F_assimfun numa função linear discriminante (LDF Fourier) resultou na melhor separação entre os dois grupos diagnósticos, com uma área sob a curva ROC de 0,90 (Figura 1). A função linear discriminante apresentou a seguinte fórmula:

LDF Fourier = -1,279 + (0,151 * minF_soma) + (0,052 * minF_fun) – (2,019 * F_assimfun)

 

 

 

 

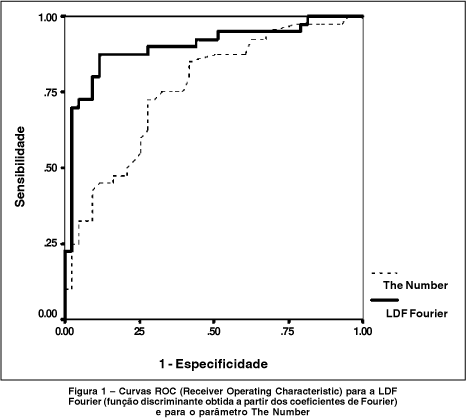
Para uma especificidade de 91%, a sensibilidade foi de 80%. Reduzindo a especificidade para 81%, a sensibilidade foi de 88%. O ponto de corte que resultou em máxima relação sensibilidade / especificidade foi 0,151 (pacientes com valor da LDF Fourier menor que 0,151 classificados como anormais). Para este ponto de corte, a LDF obteve uma sensibilidade de 88% e especificidade também de 88%. O viés estimado para a área sob a curva ROC foi pequeno, de 0,013 (1,44%).

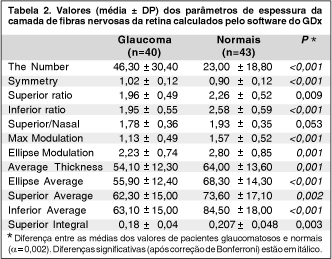
Na tabela 2 são mostrados os valores dos parâmetros de espessura da CFN calculados pelo software do GDx. Diferenças estatisticamente significantes foram obtidas para todos os parâmetros, com exceção do Superior/Nasal, Superior Ratio e Superior integral, após correção de Bonferroni. A tabela 3 mostra as áreas sob as curvas ROC obtidas para cada um dos parâmetros utilizados neste estudo. Para cada parâmetro, as sensibilidades para valores fixos de especificidade foram calculadas. Para o parâmetro The Number, a área sob a curva ROC foi de 0,76 (Figura 1), significativamente inferior à área obtida para a combinação dos coeficientes de Fourier (P = 0,002). Para uma especificidade de 91%, a sensibilidade do The Number foi de 43%, ou seja, apenas 17 dos 40 pacientes com defeitos localizados seriam detectados com esta medida. O valor do ponto de corte em 24 para o The Number resultou na melhor relação sensibilidade / especificidade para este parâmetro (sensibilidade = 72% e especificidade = 70%). O parâmetro Inferior Average obteve a maior área sob a curva ROC entre os parâmetros calculados pelo software do GDx, com 0,83. Contudo, para uma especificidade de 91%, a sensibilidade do Inferior Average foi de apenas 33%.

 

 

DISCUSSÃO

A importância dos defeitos localizados da CFN para o diagnóstico do glaucoma tem sido estabelecida por numerosos estudos. Em estudo prévio, defeitos localizados na CFN foram encontrados em olhos com aumento da pressão intra-ocular e campo visual normal, sugerindo que eles poderiam ser indicativos de anormalidade estrutural precoce no glaucoma^(36-37). De fato, anos mais tarde, alguns destes olhos vieram a desenvolver alterações no campo visual em regiões correspondentes ao defeito na CFN. Em outro estudo, foram avaliadas fotografias da CFN de 421 pacientes com glaucoma e 193 sujeitos normais, sendo encontrados defeitos localizados em 20% dos pacientes com glaucoma, e em apenas 1 olho dos indivíduos normais⁽⁶⁾. Este estudo mostra a alta especificidade dos defeitos localizados da CFN em indicar presença de alteração patológica no nervo óptico, ressaltando a importância de sua detecção em casos de suspeita de glaucoma.

Estudos experimentais têm mostrado que os defeitos localizados podem ser detectados oftalmoscopicamente quando cerca de 50% das fibras nervosas foram perdidas na região⁽⁹⁾. Isto pode ser explicado pelo arranjo dos feixes de fibra nervosa, que se dispõem de tal maneira que os axônios perdidos primeiramente no glaucoma estão localizados nas camadas média e profunda da CFN⁽⁹⁾. Assim, com a perda destes axônios, há apenas uma pequena mudança na configuração da CFN que pode não ser visível oftalmoscopicamente, pois os axônios superficiais ainda cobrem a região do defeito. Em teoria, ao medir a espessura da camada de fibras nervosas de maneira objetiva, a polarimetria de varredura a laser superaria esse inconveniente da avaliação qualitativa.

No nosso estudo, os parâmetros fornecidos pelo software do GDx mostraram uma baixa sensibilidade em detectar os pacientes com defeitos localizados da CFN, com valores variando de 15% a 48%. Ou seja, fixando-se a especificidade a 90%, os parâmetros utilizados isoladamente diagnosticaram menos da metade dos casos. Esta baixa sensibilidade dos parâmetros fornecidos pelo GDx em identificar pacientes com glaucoma inicial também foi encontrada em outros trabalhos^{(16,20,38-39)}. Em trabalho recente, os parâmetros do GDx tiveram sensibilidades variando de 7% a 40% para detectar pacientes com glaucoma (com especificidade fixa a 90%), portanto, resultados similares aos obtidos em nosso estudo⁽³⁸⁾.

Os baixos valores de sensibilidade dos parâmetros fornecidos pelo software do GDx provavelmente se relacionam a alguns fatores. Estes parâmetros em geral se baseiam em medidas de pixels compreendendo uma grande região em torno do disco óptico. Por exemplo, o parâmetro Superior Average corresponde à média de espessura dos pixels contidos em todo o quadrante superior, que abrange um total de 120°. Portanto, é provável que tal medida não se altere de maneira significativa se apenas um pequeno setor correspondente a um defeito localizado na CFN mostre redução na espessura. Parâmetros que medem relações, como o Inferior Ratio, também levam em conta espessuras englobando grandes regiões. O Inferior Ratio é calculado a partir da relação entre a média dos 1500 pixels mais espessos do quadrante inferior (compreendendo 120°) e a média dos 1500 pixels medianos do quadrante temporal (compreendendo 50°). Portanto, reduções na espessura de apenas um pequeno setor na região inferior, podem não afetar de maneira significativa a medida dos 1500 pixels mais espessos, explicando a baixa sensibilidade deste parâmetro para detecção de defeitos localizados.

A ampla variabilidade da espessura da camada de fibras nervosas nos indivíduos normais provavelmente é outro fator relacionado ao baixo poder diagnóstico dos parâmetros calculados pelo software do GDx. Assim como diversas outras variáveis biológicas, a quantidade de fibras nervosas pode variar amplamente entre os indivíduos^(27-28). Isto faz com que haja um grande intervalo de normalidade, dificultando a identificação de sujeitos que apresentam perda de fibras nervosas, mas que em valor absoluto o número de fibras e, conseqüentemente, a espessura da CFN, ainda se encontram dentro dos limites do normal. Ao fixarmos uma especificidade alta, reduzindo o número de falsos positivos, diminuímos a sensibilidade em detectar pacientes com perdas discretas na espessura da CFN. O parâmetro Inferior Average foi o que apresentou a maior área sob a curva ROC dentre os parâmetros fornecidos pelo GDx. Contudo, a sensibilidade deste parâmetro para uma especificidade de 91% foi de apenas 33%. O The Number tem sido apontado em outros estudos como o parâmetro com melhor relação sensibilidade/especificidade para o diagnóstico do glaucoma, com performance superior a do Inferior Average^{(16,18,20,38-39)}. Em nosso trabalho, o The Number teve um poder diagnóstico comparável ao do Inferior Average. Diferenças nas populações estudadas provavelmente explicam os resultados. A maioria dos pacientes glaucomatosos incluídos em nosso estudo apresentava defeitos localizados na região temporal inferior da CFN, provavelmente explicando uma melhora no poder diagnóstico de uma medida como o Inferior Average.

No presente estudo, nós avaliamos o poder diagnóstico da análise de Fourier em detectar a presença de defeitos localizados na CFN. Com uma especificidade de 91%, a sensibilidade deste método foi de 80%, superior à obtida com qualquer um dos parâmetros fornecidos pelo software do GDx. A aplicação da análise de Fourier na avaliação da forma global da curva de distribuição dos valores de espessura da CFN permite enfatizar diferenças relativas entre vários setores. Caso o GDx meça a espessura da CFN corretamente, um defeito localizado na camada de fibras nervosas deve corresponder a uma aberração na forma desta curva, não necessariamente reduzindo o valor absoluto de espessura a um nível abaixo do normal. Exemplificando, um indivíduo com altos valores de espessura em quase todas as regiões, pode ter apenas um setor com redução relativa na espessura, correspondendo a um defeito localizado. Ao invés de se concentrar em medidas absolutas de espessura, a análise de Fourier visa detectar alterações no padrão de distribuição dos valores, o que poderia ser útil para a identificação de defeitos localizados na CFN. Estudo prévio obteve sensibilidade e especificidade de 96% e 90%, respectivamente, para separação de pacientes normais e glaucomatosos utilizando uma combinação dos coeficientes de Fourier⁽³³⁾. No presente trabalho, encontramos um valor menor de sensibilidade, o que possivelmente pode estar relacionado às diferentes populações estudadas. Enquanto nós avaliamos apenas pacientes com defeitos localizados da CFN, no estudo prévio utilizando analise de Fourier este não foi um critério de inclusão ou exclusão. Defeitos localizados na CFN tendem a ser mais comuns nos estágios iniciais do glaucoma, diminuindo em freqüência com a progressão da doença⁽⁶⁾. Desta maneira, é provável que a menor sensibilidade encontrada em nosso estudo seja devida a um grau menor de dano glaucomatoso de nossos pacientes.

Diferentes métodos têm sido descritos na literatura com o objetivo de melhorar a análise dos dados de espessura da CFN obtidos com o GDx e, alguns deles, com o propósito de melhorar a identificação de defeitos localizados na CFN com este aparelho. Recente trabalho descreveu um método de análise no qual a perda difusa da CFN foi definida como uma redução na amplitude do padrão em dupla corcova da CFN, e a perda localizada foi definida como redução na correlação dos valores de espessura entre regiões que previamente haviam mostrado boa correlação em indivíduos normais⁽¹⁹⁾. Embora este método tenha resultado em sensibilidade e especificidade de 94% e 91%, respectivamente, o trabalho não avaliou uma população específica de pacientes com defeitos localizados na CFN, tornando difícil a comparação com os resultados do presente estudo. Em outro estudo, a variabilidade das medidas de espessura da CFN ao longo da elipse em torno do disco óptico foi utilizada como método para detecção do glaucoma⁽¹⁷⁾. Com a perda de espessura da CFN no glaucoma, espera-se que esta variabilidade (avaliada através do desvio-padrão das medidas de espessura) diminua. Embora este parâmetro tenha se mostrado útil para separar pacientes glaucomatosos de indivíduos normais, seu desempenho na detecção de defeitos localizados na CFN ainda precisa ser avaliado⁽¹⁷⁾.

A combinação de parâmetros do GDx em uma função linear descriminante como método para melhorar o desempenho diagnóstico deste aparelho foi recentemente proposta na literatura⁽¹⁶⁾. Uma função linear descriminante (LDF UCSD) combinando três dos parâmetros do GDx (average thickness, ellipse average e ellipse modulation), resultou em uma área sob a curva ROC de 0,887 para separar pacientes glaucomatosos de normais, com desempenho superior ao dos parâmetros quando utilizados isoladamente⁽¹⁶⁾. A aplicação da LDF UCSD à amostra de nosso estudo resultou em uma área sob a curva ROC de 0,86. Para uma especificidade em 91%, esta LDF obteve uma sensibilidade de 55%, superior aos parâmetros fornecidos pelo software do GDx, confirmando os achados sugeridos inicialmente. Outra função linear discriminante foi posteriormente proposta (LDF UNICAMP)⁽²⁰⁾, constituída por uma combinação de quatro dos parâmetros do GDx, sendo que três deles incluídos originalmente na LDF UCSD⁽¹⁶⁾, com a adição do parâmetro The Number. Em sua aplicação inicial, os autores obtiveram uma área sob a curva ROC de 0,93 para separar pacientes glaucomatosos de sujeitos normais, utilizando a LDF UNICAMP⁽²⁰⁾. Contudo, ao aplicarmos a LDF UNICAMP à nossa amostra, obtivemos uma área sob a curva ROC menor, de 0,83. Para uma especificidade de 91%, a LDF UNICAMP teve sensibilidade de apenas 53%. Embora as duas funções descriminantes acima, quando aplicadas à nossa amostra de pacientes com defeitos localizados, tenham tido desempenho superior ao dos parâmetros fornecidos pelo GDx, ambas tiveram desempenho inferior ao da LDF obtida pela combinação dos coeficientes de Fourier.

Outro fator que pode influenciar o poder diagnóstico dos vários parâmetros de espessura da CFN obtidos com o GDx resulta da compensação da polarização corneana pelo aparelho. A córnea, assim como a CFN, também apresenta propriedades birefringentes que resultam em um retardo da luz polarizada^(40-41). Para compensar o retardo produzido pela córnea, o GDx dispõe de um compensador do segmento anterior, que cancela o retardo induzido pela córnea. Este compensador assume que todos os indivíduos apresentam um eixo fixo de polarização corneana, disposto 15° nasal e inferiormente e também uma magnitude de retardo fixa (60nm). Contudo, estudos recentes mostraram que o eixo e a magnitude da polarização corneana são, na verdade, altamente variáveis entre os indivíduos, o que pode resultar numa compensação inadequada da birrefringência corneana em alguns pacientes^(42-43). Esta compensação inadequada resulta freqüentemente em exames com um aumento espúrio da espessura da CFN e diminuição no poder diagnóstico de diversos dos parâmetros fornecidos pelo aparelho^(44-45). De fato, a correção da compensação errônea da birrefringência do segmento anterior leva a um aumento do poder diagnóstico de vários dos parâmetros fornecidos pelo GDx⁽⁴⁶⁾. É possível que a análise de Fourier, por enfatizar a forma global da curva e não a espessura absoluta da CFN possa ser menos susceptível a inadequações na compensação corneana, o que poderia se relacionar ao melhor desempenho diagnóstico deste método. Em estudo recente, utilizando o GDx com compensador variável da polarização corneana, a análise de Fourier ainda assim apresentou desempenho significativamente superior ao dos parâmetros fornecidos pelo software do aparelho⁽⁴⁷⁾.

A utilização de defeitos localizados na camada de fibras nervosas como critério de inclusão em um estudo avaliando o GDx pode levar a uma superestimativa no poder diagnóstico do aparelho. Preferencialmente, critérios de inclusão baseados em características estruturais do disco óptico não devem ser utilizados para avaliação de testes que também medem características estruturais⁽⁴⁸⁾. Contudo, o objetivo primário de nosso estudo foi comparar o poder diagnóstico de diversos métodos de análise dos dados de espessura da CFN fornecidos pelo GDx. Dentro deste propósito, claramente a análise de Fourier foi superior aos parâmetros fornecidos pelo aparelho. Além disso, estudos prévios têm mostrado que a análise de Fourier também mostra altos valores de sensibilidade e especificidade quando utilizada para detecção de glaucoma em pacientes selecionados apenas com base na existência de defeito de campo visual glaucomatoso^(33,47,49).

Em suma, a utilização da análise de Fourier resultou numa melhora em relação aos parâmetros do aparelho na detecção de defeitos localizados da CFN. Tendo em vista que esta análise foi previamente validada em outras populações glaucomatosas, seu emprego parece promissor no diagnóstico do glaucoma.

 

REFERÊNCIAS

1. Sommer A, Katz J, Quigley HA, Miller NR, Robin AL, Richter RC, Witt KA. Clinically detectable nerve fiber atrophy precedes the onset of glaucomatous field loss. Arch Ophthalmol 1991;109:77-83.        

2. Jonas JB, Budde WM, Panda-Jonas S. Ophthalmoscopic evaluation of the optic nerve head. Surv Ophthalmol 1999;43:293-320.        

3. Hoyt WF, Frisén L, Newman NM. Fundoscopy of nerve fiber layer defects in glaucoma. Invest Ophthalmol 1973;12:814-29.        

4. Hoyt WF, Schlicke B, Eckelhoff RJ. Fundoscopic appearance of a nerve fibre- bundle defect. Br J Ophthalmol 1972;56:577-83.        

5. Susanna R. Nervo Óptico no Glaucoma. Aspectos oftalmoscópicos. Edusp, São Paulo, 1996, pp.48-51.        

6. Jonas JB, Schiro D. Localized wedge shaped defects of the retinal nerve fibre layer in glaucoma. Br J Ophthalmol 1994;78:285-90.        

7. Quigley HA, Katz J, Derick RJ, Gilbert D, Sommer A. An evaluation of optic disc and nerve fiber layer examinations in monitoring progression of early glaucoma damage. Ophthalmology 1992;99:19-28.        

8. Quigley HA, Reacher M, Katz J, Strahlman E, Gilbert D, Scott R. Quantitative grading of nerve fiber layer photographs. Ophthalmology 1993;100: 1800-7.        

9. Quigley HA, Addicks EM. Quantitative studies of retinal nerve fiber layer defects. Arch Ophthalmol 1982;100:807-14.        

10. Weinreb RN, Dreher AW, Coleman A, Quigley H, Shaw B, Reiter K. Histopathologic validation of Fourier-ellipsometry measurements of retinal nerve fiber layer thickness. Arch Ophthalmol 1990;108:557-60.        

11. Dreher A, Reiter K. Retinal laser ellipsometry: a new method for measuring the retinal nerve fiber layer thickness distribution. Clin Vis Sci 1992;7:481-8.        

12. Dreher AW, Reiter K, Weinreb RN. Spatially resolved birefringence of the retinal nerve fiber layer assessed with a retinal laser ellipsometer. Appl Opt 1992;31:3730-5.        

13. Zhou Q, Knighton RW. Light scattering and form birefringence of parallel cylindrical arrays that represent cellular organelles of the retinal nerve fiber layer. Appl Opt 1997;36:2273-85.        

14. Hemenger RP. Birefringence of a medium of tenous parallel cylinders. Appl Opt 1989;28:4030-4.        

15. Weinreb RN, Shakiba S, Zangwill L. Scanning laser polarimetry to measure the nerve fiber layer of normal and glaucomatous eyes. Am J Ophthalmol 1995;119:627-36.        

16. Weinreb RN, Zangwill L, Berry CC, Bathija R, Sample PA. Detection of glaucoma with scanning laser polarimetry. Arch Ophthalmol 1998;116:1583-9.        

17. Choplin NT, Lundy DC, Dreher AW. Differentiating patients with glaucoma from glaucoma suspects and normal subjects by nerve fiber layer assessment with scanning laser polarimetry. Ophthalmology 1998;105:2068-76.        

18. Susanna Junior R, Takahashi WY, Nakamura NKF. Sensibilidade e especificidade da avaliação da camada de fibras nervosas examinadas através da polarimetria a laser. Rev Bras Oftalmol 1998;57:17-22.        

19. Sinai MJ, Essock EA, Fechtner RD, Srinivasan N. Diffuse and localized nerve fiber layer loss measured with a scanning laser polarimeter: sensitivity and specificity of detecting glaucoma. J Glaucoma 2000;9:154-62.        

20. Lauande-Pimentel R, Carvalho RA, Oliveira HC, Gonçalves DC, Silva LM, Costa VP. Discrimination between normal and glaucomatous eyes with visual field and scanning laser polarimetry measurements. Br J Ophthalmol 2001; 85:586-91.        

21. Waldock A, Potts MJ, Sparrow JM, Karwatowski WS. Clinical evaluation of scanning laser polarimetry: II. Polar profile shape analysis. Br J Ophthalmol 1998;82:260-6.        

22. Medeiros FA, Leal BC, Susanna Junior R. Efeito do tamanho pupilar na medida de espessura da camada de fibras nervosas da retina com a polarimetria a laser. Rev Bras Oftalmol 2000;59:639-46.        

23. Hoh ST, Ishikawa H, Greenfield DS, Liebmann JM, Chew SJ, Ritch R. Peripapillary nerve fiber layer thickness measurement reproducibility using scanning laser polarimetry. J Glaucoma 1998;7:12-5.        

24. Duarte FB, Paranhos Junior A, Galhardo RA, Abdanur LRA, Prata Junior JÁ, Mello PAA. Reprodutividade do exame de medida da camada de fibras nervosas da retina por meio da polarimetria de varredura a laser. Arq Bras Oftalmol 1999;62:555-60.        

25. Colen TP, Tjon-Fo-sang MJ, Mulder PG, Lemij HG. Reproducibility of measurements with the nerve fiber analyzer (NfA/GDx). J Glaucoma 2000;9: 363-70.        

26. Prata Junior JA, Moura CR, Mandelo MH, Maia MB, Galhardo RA, Mello PAA. Análise da camada de fibras nervosas da retina com GDx^TM: validade diagnóstica em glaucoma primário de ângulo aberto e suspeitos de glaucoma. Arq Bras Oftalmol 2001;64:337-40.        

27. Varma R, Skaf M, Barron E. Retinal nerve fiber layer thickness in normal human eyes. Ophthalmology 1996;103:2114-9.        

28. Dichtl A, Jonas JB, Naumann GO. Retinal nerve fiber layer thickness in human eyes. Graefes Arch Clin Exp Ophthalmol 1999;237:474-9.        

29. Jindra LF, van Saarloos PP, Eikelbloom RH, Cooper RL. Fourier analysis of the nerve fiber layer by digital imaging techniques. Ophthalmic Surg 1989; 20:370-2.        

30. Bloomfield P. Fourier analysis of time series. An introduction. New York: John Wiley & Sons; 2000        

31. Cooley JW, Tukey JW. An algorithm for the machine computation of complex Fourier series. Math Comput 1965;19:297-301        

32. Zonst E. Understanding the FFT. A tutorial on the algorithm & software for laymen, students, technicians & working engineers. Titusville, FL: Citrus Press; 2000.        

33. Essock EA, Sinai MJ, Fechtner RD, Srinivasam N, Bryant FD. Fourier analysis of nerve fiber layer measurements from scanning laser polarimetry in glaucoma: emphasizing shape characteristics of the `double hump' pattern. J Glaucoma 2000;9:444-52.        

34. Steyerberg EW, Harrell FE, Borsboom GJ, Eijkemans MJ, Vergouwe Y, Habbema JD. Internal validation of predictive models: efficiency of some procedures for logistic regression analysis. J Clin Epidemiol 2001;54:774-81.        

35. DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics 1988;44:837-45.        

36. Airaksinen PJ, Mustonen E, Alanko HI. Optic disc haemorrhages precede retinal nerve fiber layer defects in ocular hypertension. Acta Ophthalmol 1981; 59:627-41.        

37. Airaksinen PJ, Heijl A. Visual field and retinal nerve fibre layer in early glaucoma after optic disc haemorrhage. Acta Ophthalmol 1983;61:186-94.        

38. Bowd C, Zangwill LM, Berry CC, Blumenthal EZ, Vasile C, Sanchez-Galeana C et al. Detecting early glaucoma by assessment of retinal nerve fiber layer thickness and visual function. Invest Ophthalmol Vis Sci 2001;42:1993-2003.        

39. Zangwill LM, Bowd C, Berry CC, Williams J, Blumenthal EZ, Sánchez-Galeana CA et al. Discriminating between normal and glaucomatous eyes using the Heidelberg Retina Tomograph, GDx Nerve Fiber Analyzer, and Optical Coherence Tomograph. Arch Ophthalmol 2001;119:985-93.        

40. klein Brink HB, van Blokland GJ. Birefringence of the human foveal area assessed in vivo with Mueller-matrix ellipsometry. J Opt Soc Am A 1988;5: 49-57.        

41. Van Blokland GJ, Verhelst SC. Corneal polarization in the living human eye explained with a biaxial model. J Opt Soc Am A 1987;4:82-90.        

42. Knighton RW, Huang XR. Linear birefringence of the central human cornea. Invest Ophthalmol Vis Sci 2002;43:82-6.        

43. Greenfield DS, Knighton RW, Huang XR. Effect of corneal polarization axis on assessment of retinal nerve fiber layer thickness by scanning laser polarimetry. Am J Ophthalmol 2000;129:715-22.        

44. Blumenthal E, Bowd C, Berry CC, et al. Increased nasal and temporal retinal nerve fiber layer thickness measurements in the GDx, a scanning laser polarimeter, are reliability "red-flags" [ARVO Abstract]. Invest Ophthalmol Vis Sci 2001;42:S118.        

45. Garway-Heath DF, Greaney MJ, Caprioli J. Correction for the erroneous compensation of anterior segment birefringence with the scanning laser polarimeter for glaucoma diagnosis. Invest Ophthalmol Vis Sci 2002; 43:1465-74.        

46. Zangwill LM, Bowd C, Greenfield DS, Weinreb RN. Correction of corneal polarization axis and magnitude improves discriminating ability of GDx nerve fiber analyzer [abstract]. Paper presented at ARVO, Fort Lauderdale, 2002.        

47. Medeiros FA, Zangwill LM, Bowd C, Bernd AS, Weinreb RN. Fourier analysis of scanning laser polarimetry measurements with variable corneal compensation in glaucoma. Invest Ophthalmol Vis Sci 2003; 44:2606-12.        

48. Garway-Heath DF, Hitchings RA. Sources of bias in studies of optic disc and retinal nerve fibre layer morphology. Br J Ophthalmol 1998;82:986.        

49. Medeiros FA, Susanna Júnior R. Análise de Fourier das medidas de espessura da camada de fibras nervosas da retina obtidas com a polarimetria a laser. Rev Bras Oftalmol 2002; 61:475-84.        

 

 

Endereço para correspondência
Felipe Andrade Medeiros
5215 Fiore Terrace #A-204
San Diego – Califórnia - 92122 - Estados Unidos
E-mail: [email protected]

Recebido para análise em 03.07.2002
Versão revisada recebida em 19.03.2003
Aprovação em 27.06.2003

 

 

Este trabalho foi realizado no Hospital das Clínicas da Faculdade de Medicina da Universidade de São Paulo – USP.
Nota Editorial: Pela análise deste trabalho e por sua anuência na divulgação desta nota, agradecemos ao Dr. Augusto Paranhos Jr.