
Helen E. Ross; Shazia Nawaz
DOI: 10.1590/S0004-27492003000600009
ABSTRACT
Objects appear enlarged in water by less than the 4/3 angular magnification. They usually appear beyond their optical distance and slightly enlarged in linear size, but not in accordance with size-distance invariance (SDI). We investigated whether misperceptions of angular size could explain the discrepancies. Twenty observers viewed targets of various sizes and distances within transparent tanks 40 cm long containing air or water. They judged distance by hidden reaching, and linear or angular size by adjusting the size of a target in air at a further distance. Matched distance was close to physical distance in air and optical distance in water. All size matches were close to true linear size, and were larger in water than in air. Angular size matches were much too small to explain departures from SDI. Size perception under water is best explained by incomplete adaptation to optical distortion, and by the use of various size cues.
Keywords: Underwater effects; Apparent size; Angular size; Apparent distance; Spatial distortion; Adaptation
RESUMO
Os objetos parecem maiores na água em pelo menos 4/3 de magnificação angular. Eles normalmente parecem mais distantes que suas distâncias ópticas e ligeiramente aumentados em tamanho linear, mas não em acordo com a invariância tamanho-distância (ITD). Nós investigamos se as percepções errôneas do tamanho angular podem explicar as discrepâncias. Vinte observadores visualizaram alvos de tamanhos e distâncias variadas dentro de tanques de 40 cm de comprimento contendo ar ou água. Eles julgavam a distância através de uma tarefa de alcance escondido, e os tamanhos linear e angular pelo ajustamento do tamanho de um alvo no ar numa distância maior. As distâncias emparelhadas foram próximas da distância física no ar e distância óptica na água. Todos os tamanhos emparelhados foram próximos ao tamanho linear verdadeiro, e forma maiores na água do que no ar. Os tamanhos angulares emparelhados foram muito pequenos para explicar os desvios em relação à ITD. A percepção de tamanho subaquática é melhor explicada pela adaptação incompleta à distorção óptica, e pelo uso de vários indícios de tamanho.
Descritores: Efeitos subaquáticos; Tamanho aparente; Tamanho angular; Distância aparente; Distorção espacial; Adaptação
INTRODUCTION
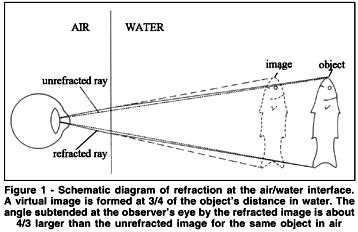
It is commonly observed that objects appear larger in water than in air, but the explanation is controversial. There is no doubt that objects are optically magnified: the refractive index of water is 4/3 that of air, and light rays are bent away from the normal on entering air from water. When the eye is at the air/water interface, the object's image is located optically at 3/4 of its distance; the object also subtends a 4/3 larger angle at the observer's eye, thus giving a correspondingly larger retinal image. For close objects viewed through a diver's facemask, the optical effects are slightly less owing to the air space in the mask. (Figure 1). However, the perceived size of objects in water is usually much less than the optical magnification, and this requires some explanation.
Predicted effects on perceived size
There are several theoretical approaches to size perception(1), and they give different predictions for the perceptual effects of the distortion. If perceived size depends only on relative size, there should be no effect; if it depends only on angular size (retinal image size), objects should appear 4/3 larger than in air; if it depends on taking account of distance, there are many possibilities. This last approach is often specified as size-distance invariance (SDI), which in its classic form states that perceived linear size is determined by perceived distance and by the true angular size. In this case, an increase in angular size under water is not a sufficient explanation for an increase in perceived linear size: an object should appear the correct (linear) size if it appears to be at 3/4 of its physical distance, or it should appear further than the optical distance and proportionately enlarged (Figure 2a).
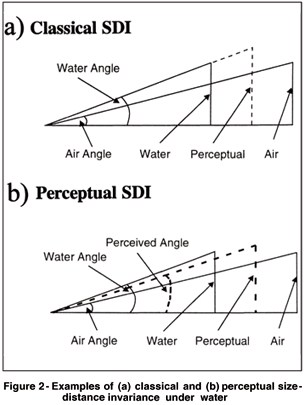
According to classical SDI, angular size is correctly encoded by the brain, and all misperceptions of linear size are caused by misperceptions of distance. Reviews of the early literature do not in general support this idea(2), and neither do recent experiments (3-4). Classical SDI also fails to explain most size illusions(5-8). In particular, it is inconsistent with the effects of viewing through telescopes and binoculars: for example, Thouless(9) found that objects appeared to be located at about twice their optical distance, but not enlarged.
There are other versions of SDI that attempt to reconcile the discrepancies. One of these depends on the concept of "perceived angular size"(5), and states that perceived linear size is a function of the perceived angular size and the perceived distance. In this version, misperceptions of linear size may occur through misperceptions of angular size or of distance, or of both. There is currently little evidence as to whether perceptual SDI holds any better than classical SDI, and the existing evidence is weak(3). It is, however, worth enquiring whether the theory could account for underwater size perception. The overestimation of linear size in water could be explained by the overestimation of optical distance combined with the underestimation of the optical angle (Figure 2b), or the correct estimation of the optical distance combined with the overestimation of the optical angle. Many other combinations are possible.
Underwater evidence
Kinney(10) reviewed experiments in which underwater objects were matched or compared with similar objects in air. She concluded that underwater objects appeared larger by approximately the optical magnification factor of 4/3, and she took this to support the angular magnification explanation. Ross(11), on the other hand, explicitly supported a modified SDI explanation. Evidence for this view was that the overestimation of linear size increased with the viewing distance, and was correlated with the overestimation of optical distance. However, the relevant ratios were not identical (size being overestimated less than the optical distance), and Ross concluded that there was some breakdown in classical SDI.
There is little evidence concerning the angular magnification explanation, because no adequate measures of perceived angular size have been made. Comparisons of true angular size can be made if two objects of different sizes and distances are displayed close to each other at the same time or in rapid succession. Thus Kinney(10) (p.86) notes that if the facemask is placed at the surface of the water and an object is viewed half through water and half through air, the underwater half appears larger. Such comparisons do not reveal how angular sizes might appear in water if there were no immediate recourse to a comparison in air. Ross(12) compared two angular sizes within one medium at a time. She had divers match the angular size of a physically larger disc to a smaller disc by increasing the distance of the larger disc, which was attached to a sliding rod. The larger disc was set too far away for an angular match, showing that its angular size was perceptually enlarged relative to the closer target. This enlargement was a factor of 2.35 in clear water and 2.20 in air. The experiment showed that angular sizes in water were perceived to increase with distance to a greater extent than in air; but the data do not allow a direct comparison of perceived angular sizes in air and water.
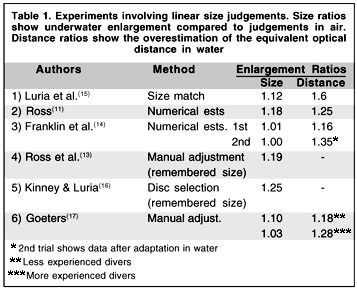
The majority of underwater experiments have required judgements of linear size rather than angular size. These experiments (summarised in Table 1) show linear size overestimation varying from 1.00 to 1.25. In general the overestimation was very much less than the angular magnification of 1.33, and also much less than would be predicted from the distance judgements according to classical SDI. The discrepancy may have been caused by the methods of measurement, or by previous perceptual learning on the part of more experienced divers, or to rapid adaptation during the course of the measurements(10,13-14). However, the results might be consistent with perceptual SDI, if the perceived angular size was less than the optical magnification (Figure 2b).
In the above experiments linear size was measured by numerical estimates of true size (in feet and inches), or by adjusting the size of one target to match another, or by adjusting or selecting a target size to match a remembered standard size (such as one foot). Experiments on eye-hand coordination offer a different method of measurement, if perceived linear size can be calculated from the end-point locations of ballistic aiming to the left and right edges of targets. Such a technique has been used to measure adaptation to underwater magnification(18), and to optically reduced size in air(19). The end-point locations can be used to measure perceived saggital distance in addition to perceived linear size; and a calculation can be made of the angular separation of the end-points subtended at the observer's eye. These calculations are useful for showing that some angular adaptation occurs, since the subtended angle reduces with viewing time in water. For example, Ross and Lennie(18) found angular adaptation of about 14 percent. However, we cannot be sure that the calculated angular size represents perceived angular size: some independent measure of perceived angular size would be needed for that.
None of the experiments reported so far offers a test of perceptual SDI: to do so would require independent measures of perceived distance, perceived linear size and perceived angular size in the same experiment. Moreover, these measures should be of compatible types, if perceptual geometry is to be upheld. Perceived angular size is particularly difficult to measure. The method mentioned above, of pointing or aiming to two angular directions, can only be used for large angular sizes. A method that could be applied to any size is to give numerical estimates in degrees, or to match the observed angle to that shown on a protractor: but most observers are very inexperienced at such estimates. More usual methods involve matching the angular size of two targets of different linear sizes at different distances. This can be achieved by adjusting the distance of a target of fixed size, or by adjusting the size of a target at a fixed distance. We decided to use the latter technique, because the same method could be used for measuring perceived linear size, by simply changing the instructions from an angular to a linear match. We also used an adjustment method (hidden reaching to a visible target) for measuring perceived distance. In this way we hoped that the measures of angular size, linear size and distance would be sufficiently compatible to provide a test of the validity of perceptual SDI.
METHOD
Participants
Twenty Psychology students from Stirling University participated voluntarily in the experiment. Five were male, and 15 female. Their age range was between 17 and 36 years, with a mean of 19.5 years. All had normal or corrected visual acuity.
Apparatus
Targets were displayed in two plastic tanks, each measuring 40 x 22 x 25 cm (Figure 3). The thickness of the plastic was 0.4 cm. One tank contained clear water and the other air. The water tank was filled almost to the top. The tanks were supported by stands (26 cm in height), which were clamped onto a bench (71.5 cm in height). There was a gap of 14.5 cm between the two tanks. A support rod, scaled in cm, was placed over the top of each tank. Squares of black Darvic were used as targets: there were two each of 2.0, 2.5, and 3.0 cm, one set for each tank. Each target was attached to a 14 cm stick with a hooked top, and could be suspended from the support rod so that it was approximately in the centre of the field of view. The rear and sides of the tanks were covered with sheets of white cardboard. The fronts of the tanks were also covered with white cardboard (to a height of 28 cm above the tanks), apart from a 13 x 13 cm viewing hole at the centre of each tank. The space between the tanks was also covered with white cardboard. These precautions were to prevent the observer from seeing the true dimensions of the tanks and the true distances at which the targets were suspended from the support rods. Beneath each tank stand was a moveable marker, initially aligned with the front of the tank. The observer could adjust the distance of the marker by moving it along a track (scaled in cm).
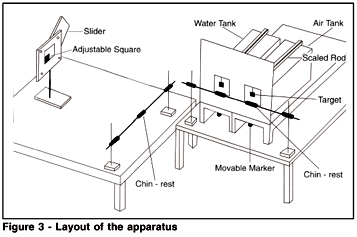
A second bench (71.5 cm in height) was located at right angles to the main bench. On it was placed a square (20 X 20 cm) made from white Darvic attached to a retort stand. The lower edge of the square was 34 cm above the bench surface. In the centre of the white square was an adjustable black square. The maximum size of the black square was 5 cm, and it could be reduced to zero by sliding an L-shaped white cover over it. The observer could adjust the size by pushing or pulling the slide diagonally, by means of a handle at the top right-hand corner of the outer square. The remaining black portion always retained the shape of a square. A ruled scale at the back enabled the experimenter to read the size of the adjusted square.
Three chin-rests were used, two in front of the tanks and one in front of the adjustable square. The chin-rests were placed at a suitable height (typically 30 cm) to enable the observer to look at the target square and the adjustable square from a horizontal viewpoint. The chin-rests were located so that the observer's eyes were 13.5 cm from the front of the tanks, and 40.5 cm from the adjustable square. The adjustable square was located further away than the furthest target, rather than nearer (as in most experiments), because of limits on the size of the tanks and on visual accommodation at very close distances. A swivel chair with adjustable height was provided to enable the observer to turn quickly between the observation tanks and the adjustable square.
The experiment was carried out in a well-lit room (4 x 60-watt fluorescent tubes), and took approximately 30 minutes to complete for each observer.
Procedure
The observers were seated in front of the apparatus and were provided with a written description of the details of the experimental procedure. They were asked to make both size and distance judgements of the various target presentations. They were instructed to keep their head as still as possible and their chin against the chin-rest whilst making judgements.
They were given a practice trial to ensure that they understood the instructions.
The targets were suspended singly at one of three distances (15, 20, and 25 cm) along the support rods. Each of the three targets (2.0, 2.5 and 3.0 cm squares) was presented at each distance in both tanks, totalling 18 presentations. Semi-random presentation orders were used. For each target presentation, the observer was asked to make three judgements. Binocular vision was used for the first two judgements (distance and linear size), and monocular vision for the third (angular size).
a) Distance. The observer was required to move the marker (hidden beneath the stand) until it was felt to be directly underneath the target square which was constantly visible in the tank. The movement was always started from the front of the tank, but the observer was allowed to overshoot and undershoot till satisfied with the match.
b) Linear size. The observer was required to vary the size of the adjustable square (initially set at 0) until it appeared to be the same physical (linear) size as the target square; that is, both squares would measure the same with a ruler. The observer was allowed only two visual size comparisons: he/she looked at the target square in the tank, then turned and adjusted the square on the trolley until satisfied with the memory match, then turned and looked again at the target square, and then made final adjustments to the adjustable square. Only the last measure was used in the data analysis. The number of visual size comparisons was limited in order to capture first impressions, and to standardise the time taken by different observers.
c) Angular size. The observer was required to vary the size of the adjustable square until it appeared to subtend the same angular size as the target square; that is, both squares would be the same size in a photograph. The procedure was the same as for linear size judgements, except that monocular vision was used in order to assist the perception of angular rather than linear size. The observer placed the preferred eye in front of the viewing hole of the tank, and used the same eye for the adjustable square. Ten observers used the left eye and 10 the right.
After the 18 trials were completed, the observers were asked to fill in a brief questionnaire regarding their awareness and understanding of the optical effects of looking into water: the answers showed that few observers had much awareness or made any conscious correction for supposed effects. The purpose of the experiment was then explained in more detail, and any questions were answered.
RESULTS
Distance judgements
The mean settings for perceived distance within the tank are shown for air and water in Figure 4. The optical distance of the targets in water was calculated as 0.75 of the physical distance in water, including the thickness of the plastic tank (0.4 cm). The settings in air correspond very closely to the physical distance, and those in water to the optical distance.
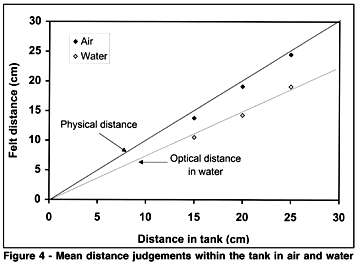
A three-way repeated measures ANOVA revealed a significant main effect due to the viewing medium, F(1,19) = 527.7, p = 0.000, water settings being closer than air settings. There was also a main effect of target distance, F(2,38) = 561.2, p = 0.000, the settings increasing with the distance. There was a significant interaction between media and distance, F(2,38) = 15.73, p = 0.000; this occurred because the absolute difference between air and water (rather than the ratio) increased at greater distances. There was no effect of target size, F(2,38) = 0.46, p = 0.640.
Objects appear enlarged in water by less than the 4/3 angular magnification. They usually appear beyond their optical distance and slightly enlarged in linear size, but not in accordance with size-distance invariance (SDI). We investigated whether misperceptions of angular size could explain the discrepancies. Twenty observers viewed targets of various sizes and distances within transparent tanks 40 cm long containing air or water. They judged distance by hidden reaching, and linear or angular size by adjusting the size of a target in air at a further distance. Matched distance was close to physical distance in air and optical distance in water. All size matches were close to true linear size, and were larger in water than in air. Angular size matches were much too small to explain departures from SDI. Size perception under water is best explained by incomplete adaptation to optical distortion, and by the use of various size cues.
Size judgements
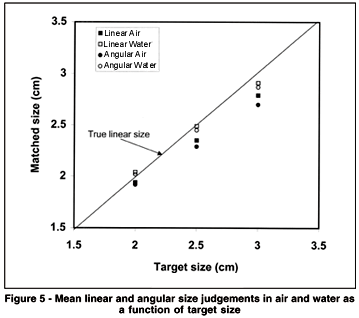
The mean linear and angular size matches in air and water are shown in Figure 5 as a function of target size. A four-way repeated measures ANOVA showed a main effect of target size, F(2,38) = 586.2, p = 0.000, the matches increasing with the true size. There was also a main effect of viewing medium, F(1, 19) = 59.96, p = 0.000, the water matches being larger than the air matches. There was no significant main effect of the type of size judgement, F(1,19) = 3.46, p = 0.078. The angular means were slightly smaller than the linear means, but this trend was the opposite of the predicted direction and was not significant on a 2-tailed test.
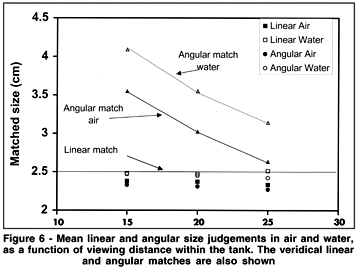
The same data are shown in Figure 6 as a function of target distance. There was no main effect of distance, F(2,38) = 1.73, p = 0.191. There was a nearly significant three-way interaction between distance, viewing medium and type of size judgement, F(2,38) = 3.14, p = 0.055, which did not seem worth pursuing.
The true linear size required for an angular match in both air and water is also indicated in Figure 5, and is very much greater than the obtained values. The true angles subtended at different distances by the mean target size (2.5 cm) were calculated taking into account the distance of the eye from the front of the tank (13.5 cm). The adjustable square (at a viewing distance of 40.5 cm) was further away than the furthest viewing distance for the targets (38.5 cm); consequently, a true angular match always required a larger linear size for the adjustable square than the target square, the difference between the two increasing at closer target distances.
Evaluation of size-distance invariance
Classical SDI did not hold precisely in air: the targets were judged to be close to their physical distance, but slightly smaller than their linear size. Classical SDI held better in water: the targets were judged to be close both to their optical distance and to their true linear size. The water judgements were thus not a simple optical transformation of the air judgements. The relationship is illustrated in Figure 7, where the ratio of judged to true linear size is plotted against the ratio of judged to true total viewing distance (in air) or to the equivalent optical distance (in water, plus 13.5 cm of air). The air and water ratios are clearly not part of the same distribution, and the water ratios are closer to SDI than the air ratios.
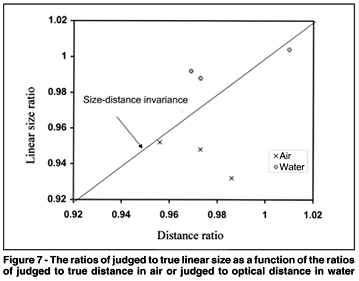
It is clear that perceptual SDI did not hold at all in this experiment, and cannot be used to explain discrepancies in classical SDI. The matched angular sizes scarcely differed from the matched linear sizes, and were much smaller than required for a true angular match (Figure 6). They were also much smaller than required for consistency with perceptual SDI. For example, the mean linear size judgement in air was 2.36 cm and the mean distance judgement was 32.6 cm from the eye, giving a required perceptual angle of 4.14 deg - but the mean angular judgement measured only 3.25 deg. Similar arguments apply in water: the mean linear size judgement was 2.48 cm and the mean distance judgement was 28.1 cm from the eye, giving a required perceptual angle of 5.04 deg - but the mean angular judgement measured only 3.46 deg.
The discrepancy from classical SDI can also be seen by comparing the water and air judgements with each other, and disregarding the physical values. The mean judgements can be expressed as water/air ratios, in the same manner as the earlier experiments listed in Table 1. The linear size ratio was 1.05, and the distance ratio (to the optical equivalent of the air distance) was 1.01. The angular size ratio was 1.07, approximately the same as the linear size ratio.
DISCUSSION
Judgements in air
The distance settings were very close to the true distance in air and the optical distance in water. This is to be expected for hidden tactile reaching at close range, with binocular vision for the target. The errors found in other experiments usually arise from the use of numerical estimates or further viewing distances.
The size settings in air were inconsistent with classical SDI in that the linear size judgements were too small in relation to the slight underestimation of distance. Under-size matches may have occurred because the adjustable and standard targets differed in some physical aspect that made the adjustable target appear relatively large. One possible factor is luminance contrast: the black adjustable square was surrounded by bright white plastic, whereas the standard targets were displayed as isolated black squares against distant backgrounds of dull white cardboard. Another possible factor is size contrast: the adjustable target was presented within a white surround (20 x 20 cm) at the same distance as the target (40.5 cm), while the standard targets were presented against a physically larger background (22 x 25 cm) at a further distance (53.5 cm). No clear predictions can be made for either contrast effect.
Other reasons for under-size matches might be procedural rather than visual. Starting position may have had an effect. The observers always adjusted the variable target upwards from zero at the start; but any bias would be small, because they typically made several adjustments before settling on a match. Another procedural bias is the "error of the standard" - the different values obtained depending on which of two targets is adjusted and which is the standard (see discussion by Kaufman and Rock(20)). However, there is usually a tendency to overestimate the standard, which is the opposite of our result. This error is often confounded with the distance of the adjustable target, which is normally closer than the standard. Our experiment was unusual in reversing the distances, and this may be a very important factor. Measurements of perceived angular size show an increase with viewing distance (7-8), and this could explain the relatively large perceived angular size (or relatively small settings) of the distant adjustable target. The discrepancy between these and previous findings may be entirely due to the reversal of the usual relative distances of the standard and adjustable targets.
Whatever the reason for the slight underestimation of the linear size of the targets, perceptual SDI might have been upheld if the angular judgements were proportionately smaller than the true angle. In fact, they were disproportionately smaller, being slightly smaller than the linear matches instead of larger. The observers appear to have had great difficulty in making angular matches, despite the use of only one eye. We have to conclude that angular size cannot be consciously perceived at such close distances, or that it cannot be measured by the method we employed(21-22).
Judgements in water compared to air
The linear size judgements in water were greater than the air judgements by a factor of 1.05, whereas the water distance judgements were almost identical to the optical equivalent of the air judgements (ratio 1.01). These results differ from the experiments reported in the introduction (Table 1), where linear size in water was overestimated less than was the optical distance. However, distance judgements were obtained for only four of these experiments, and the findings may vary with the method of measurement. Alternatively, the difference may be due to the very short viewing distances used in the present experiment.
The ratios of water to air judgements in this experiment give little support to either classical or perceptual SDI. Classical SDI was not supported because the linear size ratios were larger than the negligible overestimation of the optical distance. It could be argued that perceptual SDI was supported because the ratio of water to air angular judgements was similar to that for linear judgements. However, this argument is not convincing because the linear and angular judgements were almost identical, and the angular judgements were much smaller than the required values. The likelihood of establishing the truth of perceptual SDI remains small unless a satisfactory measure of perceived angular size can be devised.
Attempts to measure SDI rest on the assumption that there exists a unitary perceptual spatial metric that obeys the rules of geometry. The only problem, then, is how to obtain accurate and commensurate measures of perceived linear size, angular size and distance. On this view, the breakdown of SDI results from flawed measurement procedures. That assumption may be overoptimistic. There may be different spatial metrics for vision and touch, or for the dorsal and ventral visual streams (for reviews(22-23)). Furthermore, the spatial metrics (or the relation between different metrics) undoubtedly change during adaptation to optical distortions.
Explaining perceptual size enlargement
Underwater size judgements are not closely related to the magnified angular size, nor to 4/3 of the judged air size, nor to either form of SDI. The explanatory difficulties are shared by size perception in air. Do we perceive angular and linear size simultaneously; or first one and then calculate the other by taking distance into account? Introspective evidence suggests that there is only one type of perceived size at any one time, and experimental evidence suggests that it may correspond more closely to angular size under some circumstances and linear size under other circumstances. For example, McKee and Welch(21) argued on the basis of discrimination measurements that observers using normal stereoscopic vision at close viewing distances have better access to information about linear than angular size; but that for very small angular sizes (<10 arc min) the reverse is true. Kaneko and Uchikawa(24) have also argued that the two types of size judgement depend on different cues. At the short viewing distances used in our experiments, linear size judgements were more veridical than angular judgements, which implies that observers perceived linear rather than angular size. Longer viewing distances might well produce different results.
The distinction between angular and linear size has been questioned. For example, Stratton(25) (p.150-1) maintained that image size was irrelevant: rapid adaptation to optical magnification should occur, since what mattered was the relative size of all objects in the visual field. Rock(26) made a similar point regarding size transformations, while Gibson(27) (p.181) stressed the importance of relative size for normal (undistorted) visual scenes.
Our data do not provide unequivocal support for any of these views. It is probably best to abandon all geometrical approaches, and accept that perceived size is affected by a variety of factors. These factors include angular size, relative size, familiar size and perceived distance. Underwater enlargement is primarily caused by angular magnification, but its effect is reduced by all those factors that lead to perceptual adaptation.
ACKOWLEDGEMEWNTS
This project was conducted by the second author in partial fulfilment of her Honours degree requirements. We should like to thank John Russell for building the apparatus, and Ranald Macdonald for statistical advice. We are grateful to Lloyd Kaufman for comments on a draft of this paper.
REFERENCES
1. Hershenson M. Visual space perception: A primer. Cambridge: MIT Press, 1999.
2. Epstein W, Park J, Casey A. The current status of the size-distance hypotheses. Psychol Bull 1961;58:491-514.
3. Higashiyama A, Shimono K. How accurate is size and distance perception for very far terrestrial objects? Function and causality. Percept Psychophys 1994; 55:429-42.
4. Haber RN, Levin CA. The independence of size perception and distance perception. Percept Psychophys 2001;63:1140-52.
5. McCready D. On size, distance and visual angle perception. Percept Psychophys 1985;37:323-34.
6. McCready D. Moon illusions redescribed. Percept Psychophys 1986;39:64-72.
7. Ross HE, Plug C. The history of size constancy and size illusions. In: Walsh V, Kulikowski JJ, editors, Visual constancies: why things look as they do. Cambridge: Cambridge University Press; 1998, p.499-528.
8. Ross HE, Plug C. The mystery of the moon illusion: exploring size perception. Oxford: Oxford University Press, 2002.
9. Thouless RH. Apparent size and distance in vision through a magnifying system. Brit J Psychol 1968;21:339-59.
10. Kinney JAS. Human underwater vision: physiology and physics. Bethesda: Undersea Medical Society, 1985.
11. Ross HE. Water, fog and the size-distance invariance hypothesis. Brit J Psychol 1967;58:301-13.
12. Ross HE. The size-constancy of underwater swimmers. Q J Exp Psychol 1965;17:329-37.
13. Ross HE, Franklin SS, Weltman G, Lennie P. Adaptation of divers to size distortion under water. Brit J Psychol 1970;61:365-73.
14. Franklin SS, Ross HE, Weltman G. Size-distance invariance in perceptual adaptation. Psychon Sci 1970;21:229-31.
15. Luria SM, Kinney JAS, Weissman S. Estimates of size and distance underwater. Am J Psychol 1967;80:282-6.
16. Kinney JAS, Luria SM. Conflicting visual and tactual-kinaesthetic stimulation. Percept Psychophys 1970;8:189-92.
17. Goeters K-M. Die viso-motorische Orientierung des Tauchers im Greifraum in Abhängigkeit von der Erfahrung und den Sichtbedingungen im Wasser. DLR-FB 75-35. Institut für Flugmedizin, DLR Linder Höhe, D 5000, Cologne, 1975.
18. Ross HE, Lennie P. Adaptation and counteradaptation to complex optical distortion. Percept Psychophys 1972;12:273-7.
19. Scheuhammer J, Timney B. Adaptation to optically reduced size. Perception 1982;11:139-52.
20. Kaufman L, Rock I. The moon ilusion thirty years later. In: Hershenson M, editor, The moon illusion. Hillsdale: Erlbaum; 1989, p.193-234.
21. McKee SP, Welch L. The precision of size constancy. Vision Res 1992;32: 1447-60.
22. Ross HE. Levels of processing in the size-distance paradox. In: Harris LR, Jenkin M, editors, Levels of perception. New York: Springer Verlag; 2002, p.143-62.
23. Bingham GP, Zaal F, Robin D, Shull JA. Distortions in definite distance and shape perception as measured by reaching without and with haptic feedback. J Exp Psychol Hum Percept Perform 2000;26:1436-60.
24. Kaneko H, Uchikawa K. Perceived angular and linear size: the role of binocular disparity and visual surround. Perception 1997;26:17-27.
25. Stratton GM. Experimental psychology and culture. New York: Macmillan, 1903.
26. Rock I. Adaptation to a minified image. Psychon Sci 1965;2:105-6.
27. Gibson JJ. The perception of the visual world. Boston: Houghton Mifflin, 1950.
Correspondence to
Dr. Helen E. Ross
Department of Psychology, University of Stirling
Stirling FK9 4LA, Scotland
email: [email protected]