
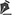
Maurice Hershenson
DOI: 10.1590/S0004-27492003000600005
ABSTRACT
A framework is proposed for analyzing the perception of motion in depth produced by simple proximal motion patterns of two to four points. The framework includes input structure, perceptual system constraints, and a depth scaling mechanism. The input is relational stimulation described by two proximal dimensions, orientation and separation, that can change or remain constant over the course of a motion pattern. Combinations of change or no-change in these dimensions yield four basic patterns of proximal stimulation: parallel, circular, perspective, and parallax. These primary patterns initiate automatic processing mechanisms - a unity constraint that treats pairs of points as connected and a rigidity constraint that treats the connection as rigid. When the constraints are activated by perspective or parallax patterns, the rigid connection between the points also appears to move in depth. A scaling mechanism governs the degree to which the objects move in depth in order to maintain the perceived rigidity. Although this framework is sufficient to explain perceptions produced by three- and four-point motion patterns in most cases, some patterns require additional configurational factors to supplement the framework. Nevertheless, perceptual qualities such as shrinking, stretching, bending, and folding emerge from the application of the same processing constraints and depth scaling factors as those that produce the perception of rigid objects moving in depth.
Keywords: Perception; Motion; Rigidity; Vectors; Depth
RESUMO
Um sistema de análise é proposto para analisar a percepção de movimento em profundidade produzido pelos padrões de movimento proximais simples de dois a quatro pontos. Este sistema de análise inclui estrutura de input, coerções do sistema perceptual, e um mecanismo de escalonamento de profundidade. O input consiste em estimulação relacional descrita por duas dimensões proximais, orientação e separação, que podem mudar ou manter-se constantes ao longo do curso de um padrão de movimento. Combinações de mudança e não-mudança nestas dimensões gera quatro padrões básicos de estimulação proximal: paralela, circular, perspectiva, e paralaxe. Estes padrões primários iniciam mecanismos de processamento automáticos - uma coerção de unidade que trata pares de pontos como conectados e uma coerção de rigidez que trata a conexão como rígida. Quando estas coerções são ativadas pelos padrões de perspectiva ou de paralaxe, a conexão rígida entre os pontos também aparenta mover-se em profundidade. Um mecanismo de escalonamento governa o grau em que os objetos movem-se em profundidade de modo a manter a rigidez percebida. Embora este sistema de análise seja suficiente para explicar as percepções produzidas por padrões de movimento de três e quatro pontos na maioria dos casos, alguns padrões requerem fatores configuracionais adicionais para complementar o sistema de análise. No entanto, as qualidades perceptuais como encolhimento, esticamento, entortamento e dobramento, emergem a partir da aplicação das mesmas coerções de processamento e dos fatores de escalonamento de profundidade que produzem a percepção de objetos rígidos movendo-se em profundidade.
Descritores: Percepção; Movimento; Rigidez; Vetores; Profundidade
This paper proposes a framework for analyzing the perception of motion in depth produced by simple proximal motion patterns of two to four points. The goal is to provide a single framework for understanding the perception of rigid object motions produced by the moving points as well as nonrigid outcomes such as shrinking, stretching, bending, and folding. The framework includes input structure, perceptual system constraints, and a depth scaling mechanism. The input consists of relational stimulation described by two proximal dimensions, orientation and separation, that can change or remain constant over the course of a motion pattern. Combinations of change or no-change in these dimensions yield four basic patterns describing the motion of two proximal points: parallel, circular, perspective, and parallax patterns. Pairs of points are processed automatically according to operating characteristics of the perceptual system described as unity and rigidity constraints. The processing includes a depth scaling mechanism to maintain perceived rigidity and induce the perception of motion in depth. Although this framework is sufficient to explain perceptions produced by three- and four-point motion patterns in most cases, some patterns require additional configurational factors to supplement the framework. Nevertheless, perceptual qualities such as shrinking, stretching, bending, and folding emerge from the application of the same processing constraints and depth scaling factors as those that produce the perception of rigid objects moving in depth.
The perception of rigid motion in depth has received so much attention since the development of computers and the concomitant interest in artificial intelligence and robotics, that a comprehensive review is beyond the scope of this paper. One major dimension that separates approaches is the type and size of the smallest proximal stimulus unit that is analyzed. The framework presented here begins with two-point motions and builds to four-point patterns. It is difficult to compare with approaches that analyze flow patterns in the optic array(1-4) or the motions produced by larger figures(5-9). Therefore, the research that is reviewed represents approaches similar to that presented here and, in many cases, the review is manifested in comparisons described throughout the paper.
The approach closest to the one being proposed is that of Johansson (for reviews(10-13)). Johansson demonstrated that elements in motion in the picture plane are always related to each other in perception and he concluded that the visual system treats motion stimulation as relational. He proposed that the visual system functions as if it performed an inverse projective geometry using components of the vectors describing the motions of elements of proximal stimulation. Johansson analyzed these vectors into common and relative components. In general, common motion describes vector components in the same direction that are equal in magnitude, and relative motion describes vector components that change the proximal distance between elements. In addition, Johansson proposed that the input components are transformed into perception according to decoding principles. He argued explicitly that, in kinetic situations, perceived size and shape constancy are automatic consequences of processes operating on the projective invariants in the proximal stimulus. In his view, motion components are automatically processed and perceived as rigidly connected units whenever possible.
Börjesson and von Hofsten(10) applied these ideas to the perceived motion of two-point proximal motion patterns. They explained the perceived motions in terms of eight basic proximal patterns: collinear and parallel common motion, collinear and parallel relative motion, and four patterns produced by combining them. Relative motion components were defined as motion toward a point or line. The magnitude and direction of the common motion components was selected such that the sum of the relative motion vectors was zero. Most of the basic patterns were consistently associated with unique perceptual responses: common motion alone was associated with the perception of motion in the frontal plane; collinear relative motion combined with parallel common motion was consistently associated with the perception of translation in depth; noncollinear relative motion alone, and combined with collinear common motion, were consistently associated with the perception of rotation in depth; and noncollinear relative motion combined with parallel common motion was associated with the perception of rotation in depth, or simultaneous rotation and motion in depth. In contrast, collinear relative motion alone or combined with collinear common motion did not produce consistent responses all possible perceived motions were reported. Similar analyses were performed for three-point patterns(14) and for rotary motion patterns(15).
Börjesson and Ahlström(16) proposed a smaller set of basic proximal motion patterns to predict the perceptions of three-point motions. They distinguished between common and relative motion in the same way, however they substituted concurrent motions for collinear relative motions. Concurrent relative motions are motion components that would meet at a point if the motion were continued. Börjesson and Ahlström also reclassified circular proximal motions. These patterns had been classified as relative motions because the vectors differ in direction (i.e., are not "common"). However, because the distance between points does not change, they were included with the common motion vectors. Combinations of these patterns produced four basic three-point motion patterns: parallel common, circular common, concurrent relative, and parallel relative motion. Börjesson and Ahlström(16) related these four vector patterns to the differential components of local surface image deformation that were proposed by Koenderink and van Doorn(3-4). The parallel common pattern contains no local deformation so the differential components are all zero. The circular common pattern is pure curl and the concurrent relative pattern is pure divergence. The parallel relative pattern is divergence and deformation combined.
The approach proposed in this paper is similar but differs in the number and type of basic motion patterns proposed, in the degree of applicability of the processing rules, and in the depth scaling mechanism that produces perceived rigidity in most cases but can also produce nonrigid perceptions as a consequence of specific configurational properties. First, with respect to basic motion patterns, the four primary two-point patterns proposed here are based solely on separation and orientation, the relational dimensions of proximal stimulation. Second, with respect to processes, the proposal is that unity and rigidity processes are always activated, the strongest possible applicability, whereas Johansson(12,17-23) proposed that unity and rigidity rules are applied whenever possible, a weaker form. Third, the proposed constraints apply only to the basic two-point patterns whereas Johansson and others(5,24) generally apply the constraints to however many points are in the proximal pattern. Finally, the strong form is accompanied by an additional requirement: perceived connections between the points that appear to be rigid (real or subjective contours) also appear to move in depth in a scaled space. This depth scaling mechanism not only maintains size and shape constancy with motion in depth, its application is also the basis for non-constancy perceptions such as shrinking, stretching, bending, and folding, and for paradoxical size-distance perceptions such as the moon illusion(25).
The analysis is presented in four sections: The first section describes the four basic proximal motion patterns. The second section describes the operating constraints necessary to link these proximal patterns to unique perceptions, and the scaling mechanism whose consequence is the perceived motion in depth. The third section illustrates the use of these concepts in explaining perceived three-dimensional motions of complex two-point patterns. The fourth section describes the perceptual consequences of combining two-point patterns to produce the perceived motions associated with three and four points. In some cases, the perceptual outcomes are straightforward combinations of the perceptions produced by the two-point patterns. In others, additional configurational factors must be introduced to explain new outcomes such as shrinking or stretching.
Basic Two-Point Motion Patterns
The motion of the endpoints of distal lines, contours, and intersections can be represented as the proximal motion of two points. In this case, however, the points do not move independently their relative position is constrained by the physical motion and the laws of projective geometry(18-19,22,26-27) (for discussions of these relationships). The consequence of this relationship is that the proximal motion of the points is a relational pattern the smallest relational pattern in the proximal stimulus. The points may or may not be connected by a proximal contour but, when they are not, subjects frequently report that the points move "as if" connected, a kind of "subjective contour" perception. In some motion patterns of three or more points, surfaces appear to bend or intersect at such "invisible" contours(10,14,28-30).
The relational structure of a specific two-point motion pattern is embodied in the proximal geometry of the vectors generated by the moving points. This geometry can be described by the proximal separation between the points and the orientation of the axis connecting them, the fundamental dimensions identified by Wallach and O'Connell(31) in their classic study of the kinetic depth effect (KDE). Separation describes the proximal distance between the points over the course of the motion. It is specified as visual angle or retinal size, the envelope of the impinging light pattern. Orientation describes the proximal meridian of the axis connecting the points over the course of the motion1. These are relational dimensions: separation relates the points to each other and orientation relates the position of the axis to itself over time.
Proximal separation and orientation are independent dimensions that may change or remain constant over the course of the motion. For two-point motion patterns, change in separation and orientation can be understood unambiguously. However, the situations in which the dimensions remain constant require clarification. Constant separation means that the distance between the points does not change as they move. Constant orientation means that the proximal orientation of the axis connecting the points does not change as they move. Thus, although the motion of the points produces a change in the proximal position of the axis connecting the points, the orientation of the axis remains the same. Consequently, for all basic motion patterns, the axis connecting the points changes its proximal position in some way(31) even when the relational dimensions do not change.
The four types of proximal patterns produced from combinations of these dimensions are illustrated in figure 1. They constitute the perceptual atoms, the relational units of proximal stimulation2. Each combination produces a unique proximal pattern: A parallel pattern (Panel A) is produced when both proximal dimensions are constant; a circular pattern (Panel B) is produced when orientation changes while separation remains constant; a perspective pattern (Panel C) is produced when separation changes while orientation remains constant; and a parallax pattern (Panel D) is produced when both dimensions change. The basic patterns produced by changing orientation (circular and parallax patterns) require that one of the points remains stationary because, when both points move, an additional component is introduced into the motion pattern. Individually, the four basic proximal patterns produce unique perceptual responses. In general, however, constant proximal orientation is associated with perceived translation and changing proximal orientation is associated with perceived rotation; constant proximal separation is associated with perceived motion in the frontal plane and changing proximal separation is associated with perceived motion in depth.
The four basic proximal patterns proposed here are similar to those obtained from analyses in different but related contexts. Geometrical and mathematical analyses of optic flow(1-4), psychophysical studies of detector mechanisms(32), and physiological studies of single-cell responses to visual stimulation(33) have focused on similar patterns to describe four basic proximal motions: rigid translation (parallel pattern) and rotation (curl, circular pattern), expansion/contraction (div, perspective pattern), and shear (def, parallax pattern). The basic patterns proposed here are different because they are relational patterns between pairs of moving points, not independent vectors or collections of vectors such as flow patterns. They are two-dimensional spatio-temporal patterns that embody the continuing relationship between the two points over the course of their motion.
Parallel pattern. The parallel pattern (Panel A) contains no relative motion. The separation between the two moving proximal points remains constant over the course of the motion (A1B1 = A2B2). The orientation of the axis connecting the points remains constant because the points move at the same rate along parallel paths in the same direction. (Parallel vectors in opposite directions do not maintain a constant separation and, therefore, constitute relatively complex patterns. A pattern of this type is analyzed in the third section.) In the laboratory, parallel patterns of continuously oscillating dots(10) or stroboscopically presented points of light(29) produced consistent perceptual responses they appeared to move in the frontal plane as if connected by a rigid object.
Circular pattern. In the circular pattern (Panel B), the distance between the points remains constant (AB1 = AB2) but the proximal orientation changes over the course of the motion. The consequence of this combination is that one point (A) remains fixed, while the other rotates around it in a circular path. The vector describing the motion of point B is perpendicular to the axis connecting the points throughout the course of the motion. Perceptual responses to circular patterns are also consistent: the points appear to be connected by a rigid contour that moves in a circular path in the frontal plane around point A, the fixed end(18,34-36).
Perspective pattern. In the perspective pattern (Panel C), the distance between two proximal points changes (A1B1 A2B2) while proximal orientation remains constant, i.e., the axis connecting the points remains in the same proximal meridian throughout the course of the motion. Perspective patterns produce consistent responses that described perceived translation in depth or translation and rotation in depth of an invisible rod connecting the dots(10,29)3. The direction of the separation-change determines the direction of the perceived motion in depth: converging vectors produce perceived motion away from the viewer and diverging vectors produce perceived motion toward the viewer.
When the points move directly toward or away from each other at the same rate, the vectors are equal, collinear, and in opposite directions. This pattern is called a linear size-change pattern. In isolation, linear size-change patterns do not produce unique perceptual responses. Responses may include perceptions of a linear extent that changes size in the frontal plane, that moves in depth toward or away from the viewer, or that rotates in depth around the point of symmetry(10,29,31,37-39). In combination, however, linear size-change patterns play an important role in understanding nonrigid perceptions such as shrinking and stretching (see below).
Parallax pattern. The parallax pattern (Panel D) is produced when both proximal separation and orientation change, i.e., the distance between the points changes and the axis connecting the points changes its proximal orientation throughout the course of the motion. This pattern consists of a stationary point (A) and a moving point (B). The end of the contour at A appears to be stationary because point A is fixed in the proximal stimulus. Therefore, point A is the point of rotation of the contour. When the vector describing the motion of point B is perpendicular to the axis connecting the points (90- or 270-deg relative orientation), a circular pattern is produced; when the vector and axis are collinear (0 -or 180-deg relative orientation), an asymmetrical size-change pattern results4. Therefore, parallax patterns are produced when point B moves in any direction other than these.
Parallax patterns produced consistent responses that described perceived rotation in depth about the stationary end(10,29). The direction of perceived rotation is determined by the direction of the separation change: Decreasing separation produces perceived rotation in depth (B end of the contour) away from the depth plane containing point A, i.e., an increase in the relative depth orientation of the contour; increasing separation produces perceived rotation in depth toward the depth plane containing point A, i.e., a decrease in the relative depth orientation of the contour.
Comparison of Vectors
Börjesson and von Hofsten(10) proposed a subset of basic vector patterns based on Johansson's conceptions and their proposal has been elaborated in subsequent formulations(10-12,16,39). Although there is an obvious similarity between the eight motion patterns they described and those proposed here, there are important differences. In Börjesson and von Hofsten's(10) system, the magnitude and direction of the common motion components (similar to parallel motions) were selected such that the sum of the relative residual motion vectors is zero. The consequence of the summation constraint is that the components are not independent each specific set of relative motions defines a specific set of common motion vectors for however many points are being analyzed. Furthermore, the definition of relational motion includes not only the motion of two points relative to each other (collinear vectors), but also relative motion toward an external point or line(10,16).
In contrast, the basic patterns proposed in Figure 1 are defined exclusively in terms of two independent proximal properties: separation of the points and orientation of the connecting axis. Furthermore, separation relates the points to each other, rather than to a third, possibly unrelated aspect of the proximal geometry such as an external point or line, and orientation relates the connecting axis to itself over time. They also differ because complex patterns consisting of three or more points can be analyzed in terms of the basic two-point patterns rather than as sets of motions converging toward a common point or line. Finally, specific combinations of the basic patterns can be associated with unique perceptual outcomes such as shrinking(28) and stretching or bending (see below).
LINKS BETWEEN BASIC PROXIMAL MOTION PATTERNS AND PERCEPTION
The four motion patterns are the simplest relational units in the proximal stimulus that produce consistent perceptual responses. But proximal stimulus structure alone does not determine unique perceptual responses. There must be activity of the perceptual system mediating between the structure in the proximal pattern and the structure in perception. These perceptual mechanisms are the unity and rigidity constraints, and a scaling mechanism that governs the perceived motion in depth while maintaining constancy.
Automatic Perceptual Processes: Structural Constraints
Structural constraints are operating characteristics of the perceptual system. They represent processes that are initiated automatically whenever stimulated by one of the four basic two-point motion patterns. Two types of structural constraints are proposed: unity and rigidity. The unity constraint is the mediating perceptual activity that makes two moving proximal points appear to be connected. The rigidity constraint is the mediating perceptual activity that makes the apparent connection between two proximal points appear to be rigid. Because concepts such as "unity" and "rigidity" have a long history in the literature on visual perception, a comparison with all definitions is beyond the scope of this paper (for a brief recent history(3)). Instead, structural constraints are compared with two related systematic concepts "decoding principles" proposed by Johansson(12,17-23) and "internal constraints" proposed by Shepard(40-42). One major distinction should be clear, however, the constraints proposed here refer to mechanisms that operate on pairs of proximal points. Therefore, the proposal is different from analyses that rely on a rigidity assumption applied to entire configurations or anything more than a pair of points(5,24,43-44).
There is an interesting and important point that must be emphasized if the rigidity constraint proposed here is to be properly understood. The fact that nonrigid perceptions occur should not be taken as evidence that the rigidity constraint has not been operating. Indeed, a major hypothesis of this paper is that the rigidity constraint is always operative (by definition of a structural constraint) and that, in certain situations (due to other factors), the object in perception does not appear to be rigid. In other words, the end product of a sequence of processes that includes a rigidity constraint may not be a rigid object in perception. The goal of explanation is to uncover those aspects of the processing sequence that determine the nonrigid perception, given the operation of the constraint. For example, with respect to shrinking, the unusual aspect of the situation is the linear size-change component of the three-point motion pattern(28); with respect to stretching, it is the constant vertical dimension given a linear size-change pattern in the orthogonal (horizontal) dimension (see Figure 8). The occurrence of these nonrigid perceptual outcomes should be taken as support for the strong form of the rigidity constraint in the context of the explanatory framework rather than as evidence against it.

Shepard(41) proposed that, during mental transformation of its orientation or position in space, the structure of an imagined object is preserved by "internalized constraints," the same constraints that govern the motions and positions of objects in perception. He proposed, moreover, that these constraints match external constraints describing the three-dimensional motion of distal objects. One obvious difference is that the structural constraints proposed here describe the relationship between proximal motion patterns and perceived motions whereas Shepard's internalized constraints describe the motions of distal objects. The proposed constraints are also clearly different from Johansson's decoding principles because structural constraints apply only to two-point basic patterns whereas decoding principles have been applied to two or more proximal points simultaneously. These differences have important consequences for the pervasiveness of the constraints. Like many researchers on mental imagery, apparent motion, and kinetic depth, Shepard assumed that distal objects were rigid ("global" rigidity). However, applied to perception, the strong form of a global rigidity hypothesis is untenable(5,43). Consequently, both Johansson and Shepard limited their conception of constraints by making them more or less operative so that certain outcomes were "preferred" but not always manifested.
In contrast, the structural constraints proposed here describe only processes initiated by the four basic two-point motion patterns. Limited in this way, the constraints can be made more pervasive: they are initiated whenever stimulated by one of the four basic patterns. The constraints apply to larger patterns only within the context of these patterns as manifested in pairwise analysis. Thus, by limiting the domain of application, a strong form of the constraint can be reinstated, and it is not necessary to invoke "assumptions" or "heuristics" applied by an "executive" to explain unity or rigidity as a visual "preference" or "interpretation"(6,8,45-48). This approach has the added advantage of providing an explanation for nonrigid perceptions (e.g., shrinking, stretching, bending, and folding) while maintaining a strong form of the rigidity constraint in combination with a depth scaling mechanism.
Another difference is derived from the fact that Shepard's constraints are axioms of geometry describing three-dimensional paths of distal object motions whereas structural constraints, like Johansson's principles, describe proximal-perceptual relationships. Processes that relate proximal structure to perceptual structure reveal the emergent nature of some aspects of perception such as contour and depth. By definition, emergent qualities do not have correlates in the proximal stimulus, i.e., they are not necessarily coded in the optic array(19-20).
The final comparison refers to the primacy of the constraints. Both Johansson and Shepard proposed that perceived motion in depth was primary and that unity and rigidity were secondary qualities of perception. The proposal here is that unity and rigidity are primary because they are the direct result of automatic perceptual activity, the structural constraints, and that motion in depth is secondary because it is a consequence produced by that activity when initiated by a specific subset of proximal patterns. This difference in primacy is another advantage provided by the strong form of the rigidity constraint.
Scaling Mechanism and Perceived Motion in Depth
The structural constraints mediate between structure in the proximal stimulus (basic patterns) and the structure in perception. They describe processes that produce a perceived rigid connection between two points given the changing relative positions of the points in the proximal stimulus. When the proximal distance between the points is constant, the perceived rigidity simply reflects an unchanging component of the proximal stimulus. Therefore, no additional changes are required in the perceptual qualities associated with the points they appear to be endpoints of a rigid object moving in a frontal plane.
However, when the proximal distance between the points changes, the distance between them can appear to remain constant only if their perceived motion is carried into a depth dimension. But the relative amount of motion in depth necessary to maintain rigidity must also be controlled. Thus, there must be a scaling mechanism that operates to transform the changing proximal extent into a contour or surface of constant perceived size whose position in depth changes appropriately(1,25). This contingent relationship between changing retinal area and changing perceived depth has been embodied in a proposed kinetic invariance hypothesis: An expanding or contracting solid visual angle (proximal stimulus structure) produces a constant perceived size and a changing perceived distance(25). When these relationships are not maintained, for whatever reason, nonrigid perceptions resultobjects appear to shrink or stretch, to bend or fold.
The classic relationship relating perceived size to perceived distance is in a static form. Introducing motion into the analysis of size-distance relationships made it necessary to separate two aspects of the perception of sizethe perceived rigidity of a contour or surface had to be separated conceptually from its perceived metric size. That is, in its traditional usage, size constancy means that an object does not change in perceived size but, in kinetic situations, the phenomenal experience is better described as perceived rigidity. Metric size judgments could then be understood as reflecting the scale that produces the altered position in three-dimensional space. Thus, an object may appear rigid, i.e., appear to be unchanging in size, yet produce different metric size judgments when in different positions in depth(25).
Perceived shape and shape constancy were not included in the original analysis of the kinetic invariance hypothesis. Nevertheless, it should be clear that the same relationships hold: shape constancy could be redefined as the perception of rigid objects rotating in depth and could be separated from a perceived metric used to index shape. This point is strikingly illustrated in an experiment by Loomis and Eby(49) in which subjects judged the apparent length of cylinders whose axis of rotation oscillated in depth. Judged length increased with range of oscillation, suggesting to Loomis and Eby that there was a failure of shape constancy. However, the subjects reported that the cylinders did not appear to be changing in shape, they appeared rigid. In the context of this analysis, the responses would be interpreted as judgments of metric size of an apparently rigid cylinder that was oscillating in depth. A similar distinction was manifested in studies of the metric structure of shapes moving in slanted planes(50-51). Once again, the metric measurements varied, but subjects reported that the shapes appeared to be rigid.
COMPLEX TWO-POINT PATTERNS
The basic patterns can be combined to produce complex two-point motion patterns and, conversely, complex patterns can be decomposed into the basic patterns. Two motion patterns have been selected to illustrate the analysis. These patterns are especially informative because, despite their relatively simple geometric structure, they represent complex stimuli for perception.
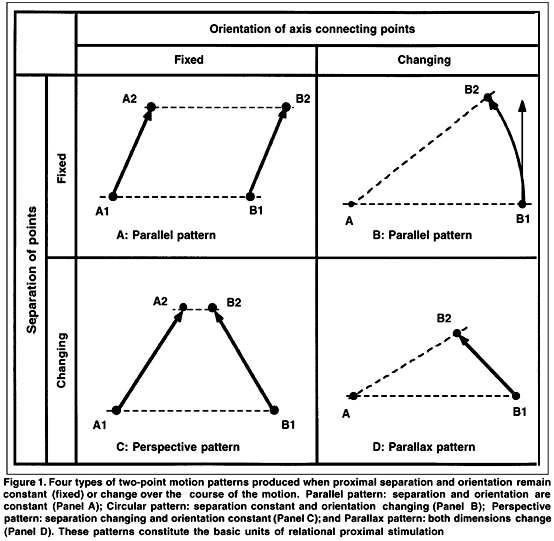
Perspective/parallax Patterns
Panel A of Figure 2 shows a perspective/parallax pattern: The separation between two points decreases, and the axis connecting the points changes its proximal orientation throughout the course of the motion. The motion of the points can be described by a pair of unequal converging vectors. Experimentally, this pattern produced responses that were divided between two categoriessimultaneous translation and rotation in depth, and simple rotation in depth of the connecting rigid object(10,29).
Panel B shows the perspective/parallax pattern analyzed into basic pattern components: a perspective pattern and a parallax pattern. The perspective pattern accounts for the component of motion of point B that corresponds to the motion of point A. This component of the pattern is associated with the perceived translation in depth. The parallax pattern accounts for the change in orientation of the axis connecting points A and B and is associated with perceived rotation in depth.
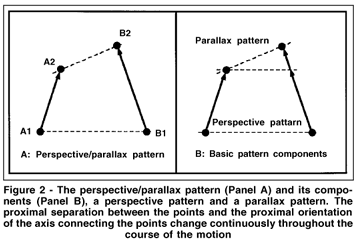
Parallel Motion in Opposite Directions
Figure 3 shows two points moving at the same rate along parallel paths in opposite directions. The separation between the points changes continuously and the orientation of the axis connecting the points also changes continuously. In experiments, this motion pattern produced consistent responses rotation in depth, or rotation and translation in depth of a rigid object(10,29).
Because the vectors are equal, the instantaneous positions of the two moving points remain equidistant from a single stationary point (P). The basic pattern components are readily apparent from the figure: The pattern is a combination of two congruent parallax patterns whose points of rotation are at P. It is interesting to note that, because both patterns rotate about the same point, two perceptions are possible: the rigid contour connecting A and B could appear to rotate about point P, or two rigid contours (AP and BP) could form a V-shaped line that opens and closes in depth ("bookfold" motion). In the former case, point P is the point of symmetry of the motion pattern and the center of rotation of the contour connecting A and B. In the latter case, the two parallax patterns act independently to produce a single perceptual response. The evidence is clear, however. In experiments, the predominant perception described a single rigid line connecting the points (bookfolding was never reported). In either case, the direction of the change in separation determines the direction of the perceived rotation in depth or perceived opening and closing of the perceived contours. Decreasing separation results in perceived rotation in depth that increases the depth angles, and increasing separation results in perceived rotation in depth that decreases the depth angles.
THREE AND FOUR PROXIMAL POINTS
Three-point proximal motion patterns may appear to be moving surfaces (objects) defined by edges that connect the points. The surfaces may appear to be rigid or may appear to change in some way. In the proposed analysis, three-point patterns are treated as composites of two-point patterns. They are analyzed pairwise using the structures described in the two-point analysis and the associated conceptual framework. However, an additional factor must be taken into accountthe relationships among the two-point patterns. These relationships are described by configurational characteristics. For example, the three two-point patterns in a three-point motion pattern may converge toward the same point or toward different points; the convergence point(s) may be inside or outside the area defined by the axes connecting the points or it may be on one of the axes. These configurational factors affect the perceptual outcomes, i.e., they play a role in determining whether the object (surface) appears rigid or changes in some way. Thus, the strong forms of the unity and rigidity constraints can be applied to the relationships between pairs of points (the edges of the surfaces) because the global perceptual changes can be attributes to the configurational factors.
Combining Perspective Patterns
Perceived rigid surface moving in depth. Figure 4 shows two three-point patterns that converge toward a point. The points move from an initial position (A1, B1, C1) at t1 to a terminal position (A2, B2, C2) at t2. In Panel A, the convergence point is within the triangular area specified by the points and, in Panel B, the convergence point is outside the triangular area specified by the points. Patterns of three or more points that converge toward a single point are called contraction patterns; those that diverge are called expansion patterns.
The pairwise analyses of the patterns in Figure 4 reveals three perspective patterns whose points of convergence coincide (point P). In isolation, the perspective patterns appear to be rigid contours moving in depth toward point P. In combination, the points appear to be a rigid unit, a surface (ABC) or an object moving in depth toward point P. An expanding pattern is perceived as an approaching rigid surface and a contracting pattern is perceived as a receding rigid surface(1,14,25,29,46,52-57). Thus, both the unity and the rigidity constraints and a depth scaling mechanism operate for these three-point patterns to produce the perception of a rigid object moving in depth.
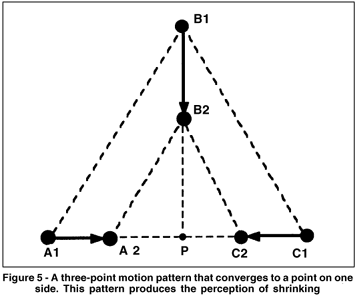
Perceived shrinking in a constant depth plane. Figure 5 shows a three-point motion pattern that converges toward a point (P) on one side of the triangular area formed by the points. The points move from an initial position (A1, B1, C1) at t1 to a terminal position (A2, B2, C2) at t2. This pattern is unique because the motion converges toward a point (P) on one of the axes connecting the points. The pairwise analysis of these motions reveals how they differ from the patterns in Figure 4. Here there are only two perspective patterns (AB and BC) whose points of convergence coincide. The motion of the third pair of points is a decreasing linear size-change pattern (AC) whose point of convergence coincides with those of the perspective patterns. In isolation, the relative motions of the perspective patterns (AB & BC) appear to berigid contours moving in depth toward point P. The linear size-change pattern alone does not produce a unique perceptual outcome but, in combination, it has a unique effect on the perception of the three-point configuration.
In experiments, this motion pattern consistently produced the perception of a two-dimensional figure shrinking in size in a single depth plane(28). Thus, the combination negated the perceived rigidity of the perspective substructures, and carried the changing size (shrinking) as a perceived property of the entire object (Figure). The perceived motion in depth associated with the perspective structures was also negatedthe shrinking object appeared to remain in a single depth plane. These consequences were independent of the type of background (blank or texture gradient) and of the orientation of the figure, i.e., whether the convergence point was on the top, side, or bottom of the figure. Furthermore, the motion of the points appeared to be part of a unit (a surface or object) whose size was changing. This outcome illustrates the point that an analysis based only on two-point structures is not sufficient to predict the perceptual response to three-point patterns. In this case, the three two-point motion patterns produced a unique feature in the global pattern convergence toward a point on one side and this feature produced a unique perceptual outcomeperceived shrinking.
One final consequence of this analysis should be emphasized. The proposed depth scaling mechanism describes a relationship between perceived rigidity and perceived position in depth. This contingency has been demonstrated by comparing responses to patterns similar to Figures 4 and 5. When the point of convergence was on a side, the predominant response described a shrinking object whose position in depth remained fixed in a single depth plane; when the point of convergence was near the center, the predominant response described a rigid object moving in depth(28). The contingent relationship between perceived rigidity and perceived depth-change bears on our understanding of minimum principle explanations of space perception(7,58). Under a minimum principle, the most parsimonious organization of the input determines the perceptual response. In this view, the center-convergence pattern appears to move in depth and the side-convergence pattern appears to shrink because these perceptions require change in only one dimension: z-axis for the former and size for the latter. But this explanation masks the more important feature of the responsesthe absence of change (constancy) in perception, which, in this case, is manifested as perceived rigidity (constancy of size and shape) and position constancy (motion in a single depth plane). Hershenson's(28) experiments demonstrated these relationships explicitly because the dual forced-choice response exposed the contingent relationship. In the limiting cases, change in one perceptual attribute was associated with constancy in the other: changing perceived size (shrinking) with constancy of depth plane position and changing position in depth with nonchanging size and shape (constancy or rigidity). In this sense, a rigidity constraint and a minimum principle are the same when they refer to a single size-position continuum.
Combining Parallax Patterns
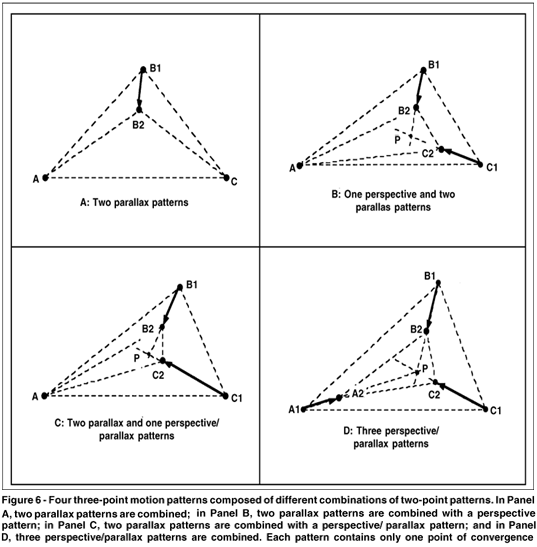
Figure 6 shows three-point motion patterns that combine parallax and perspective patterns in different ways to produce different perceptual outcomes. Note that the motions converge toward a single point in Panels B, C, and D.
Perceived rotation in depth around a side. Panel A of figure 6 shows a three-point pattern consisting of two stationary points (A and C) and one point (B) moving directly to-ward the axis connecting the stationary points. The pairwise analysis shows that this pattern is produced by the combination of two parallax patterns (AB and AC). In isolation, the parallax patterns appear to rotate in depth around the stationary points A and C, respectively. Responses to this global pattern described a rigid triangle rotating in depth or moving in the frontal plane(29). When rotation in depth was reported, point B appeared to move in depth away from the depth plane of side AC, toward or away from the viewer. Thus, AC served as an axis of perceived rotation for the surface ABC, and contours AB and BC appeared to rotate in depth around the stationary points A and C, respectively. When outline triangles were the stimuli, the presence of this unchanging contour (AC) may have anchored the combined perception in a fixed depth plane, thereby negating the motion-in-depth components. Although descriptive responses were not recorded, based on the outcome of the experiments on shrinking, it is likely that the triangle also appeared to change shape when the perceived motion was limited to the frontal plane (anecdotal observations support this interpretation).
Combining Perspective and Parallax Patterns
Perceived rotation in depth around a fixed vertex. Panel B of figure 6 shows a three-point pattern consisting of a stationary point (A) and two points (B and C) converging toward a point (P) within the triangular area (ABC). The axis connecting points B and C remains in the same proximal orientation throughout the course of the motion. The pairwise analysis reveals two parallax patterns (AB and AC) and a perspective pattern (BC). In isolation, the parallax patterns appear to rotate in depth around the fixed point A, and the perspective pattern appears to move in depth toward point P. In combination, the points should appear to be a rigid triangular surface (ABC) whose side (BC) rotates in depth away from the depth plane containing point A, a stationary vertex of the surface. Outline triangles moving in this way were primarily described as a rigid surfaces rotating in depth. Light points were also described as a rigid surface, but the motion most frequently reported was simultaneous translation and rotation in depth (Hershenson, 1993). Thus, in this pattern, the presence of the outlines apparently supported the more precise perception of the translation motion of BC. Furthermore, the translation motion of the light point patterns could easily appear to have a rotation component because only a slight change in the orientation of the connecting axis would be required.
Perceived twisting in depth around a fixed vertex. Panel C of figure 6 shows a three-point pattern consisting of a stationary point (A) and two points (B and C) converging toward a point (P) within the triangular area (ABC). The axis connecting points B and C undergoes a constant change in proximal orientation throughout the course of the motion. The pairwise analysis reveals two parallax patterns (AB and AC) and a perspective/parallax pattern (BC). In isolation, the parallax patterns appear to rotate in depth around the fixed point A, and the perspective/parallax pattern appears to move in depth with a twisting motion toward P. In combination, the points should appear to be a rigid triangular surface (ABC) whose side (BC) moves in depth with a twisting motion away from the depth plane containing point A, a stationary vertex of the surface. Thus, the entire surface should appear to twist in depth around A. This pattern has not been studied experimentally but anecdotal observations corroborate this outcome.
Perceived translation and rotation in depth. Panel D of figure 6 shows a pattern consisting of three points converging at different rates toward a point (P) inside the triangular area. The axes connecting the points change their orientation throughout the motion. The pairwise analysis reveals three perspective/parallax patterns that are not congruent. In isolation, these patterns appear to be rigid contours simultaneously rotating and translating in depth. The combination should appear to be a rigid triangular surface (ABC) that is simultaneously rotating and translating in depth toward point P. In experiments, this pattern was described as a rigid triangle simultaneously translating and rotating in depth or simply translating in depth(25,29).
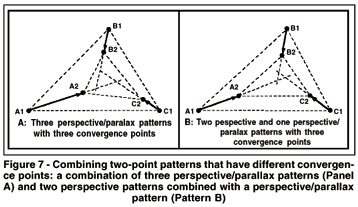
Perceived change of shape with motion in depth. Figure 7 shows two three-point patterns that converge to three different points within the triangular area specified by the three points. Pairwise analysis of the pattern in Panel A shows three perspective/parallax patterns, a combined proximal stimulus that produces the perception of a rigid surface simultaneously translating and rotating in depth(14). Panel B shows an impossible combination. The pairwise analysis reveals that this pattern is composed of two perspective patterns (AB and AC) and a perspective/parallax pattern (BC). In isolation, the perspective patterns (AB and AC) move in translation in depth and the perspective/parallax pattern (BC) moves in depth simultaneously in translation and rotation. In combination, this proximal pattern presents an "impossible" perceptual stimulus: If the two perspective structures produce perceived translation in depth of two of the contours of a perceived rigid triangular surface (ABC), the third contour cannot simultaneously rotate in depth. In other words, the pattern cannot be organized perceptually as a moving surface that remains rigid and simultaneously one that moves in the manner required by the components of the proximal motion pattern. Thus, the pairwise analysis reveals an aspect of the motion pattern that is not immediately apparent from analysis of the global configuration. This pattern has not been studied experimentally, but it should be perceived as a surface that moves in translation in depth and simultaneously changes in shape. Anecdotal observation by the author and many students corroborate this outcome.
Combination and competition. Todd(9) used displays of three connected line segments whose endpoints moved along randomly generated elliptical or hypertrochoidal trajectories. The stimuli were perceived as three rods moving in space. However, the connections between the rods could appear to be rigid or nonrigid, a distinction easily made by subjects. When the framework of this section is used to analyze the stimuli, the motion of two connected line segments defines a three-point motion pattern. Therefore, the total pattern produced by the three line segments is a combination of two interconnected three-point patterns. The perceptual outcomes can be predicted directly from this combined three-point analysis.
Börjesson & Ahlström(16) studied the "grouping power" (unity) of their four basic three-dot motion structures by placing them in competition with one another. Their stimuli contained two three-dot motion patterns that had one dot in common, i.e., one dot in one pattern moved in exactly the same way as one dot in the other pattern. The common dots from the two structures were superimposed in the stimulus so that the total stimulus consisted of five dots. Subjects reported which three-dot pattern appeared most stable. The results show that three-dot structure is an important determiner of grouping: parallel and circular common motions (parallel and circular patterns) had the strongest grouping power and parallel relative motions (parallax pattern) had the weakest grouping power. Thus patterns that produce perceived motion in the frontal plane capture a common dot more easily than those that produce perceived motion in depth. Although this is important information for understanding the perceptual organization of displays with more than three dots, it does not impact on the understanding of perceived motion associated with three-point displays per se. Nevertheless, because motion in the frontal plane predominates when there is competition between patterns, these data support the suggestion that the perception of depth is secondary.
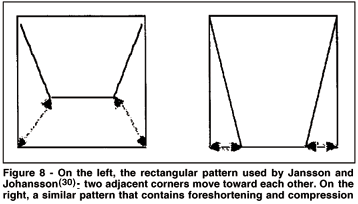
Four proximal points. Four-point motion patterns may be analyzed in terms of the two- and three-point patterns described in the previous section. Recall that the analysis of those patterns rested on the two-point analysis, the structural constraints, the scaling mechanism, and configurational considerations that reflect the manner in which two-point patterns combine to produce the three-point patterns. Similarly, the analysis of four-point patterns considers configurational aspects that reflect the manner in which three-point patterns combine to produce four-point motions. Jansson and Johansson(30) described rectangular figures as four-point motion patterns by treating the corners as moving points and the sides as visible axes connecting the points. A detailed analysis of their figures is beyond the scope of this paper. However, the pattern in which two adjacent corners move towards each other (Figure 8, left pattern) warrants discussion because it illustrates an additional consequence of this analysis. In Jansson and Johansson's experiment, this pattern produced responses that described a surface that appeared to be stretching or bending.
The analysis of this pattern shows that that the motions of the corners produce a linear size-change pattern. When this motion is organized as part of the global rectangular pattern, the figure appears to stretch as it rotates in depth around the fixed lower side. To understand this response, recall that a change in separation between proximal points is associated with motion in depth, and that the rigidity constraint and depth scaling mechanism operate to maintain the perceived rigidity of the object in motion. But the scaling mechanism operates in response to stimulation over a retinal area, not linear stimulation alone(25). Therefore, for a rectangle rotating around a horizontal axis, there must be a change in at least two meridians: change in the horizontal meridian called foreshortening, and change in the vertical meridian (altitude of the quadrilateral) called compression. In figure 8, the pattern on the right contains both of these changes, and in normal situations, a proximal motion pattern such as this (i.e., containing compression and foreshortening) produces consistent reports of a rigid surface rotating in depth about a horizontal axis.
In contrast, the pattern on the left contains foreshortening but no compression. The altitude of the rectangle, the separation between the two horizontal sides, does not change. To maintain perceived rigidity in the vertical dimension, the vertical separation must change by an amount appropriate for the rigidity constraint to operate within the scale provided by the changes in the horizontal dimension (and vice versa). In this case the depth-scaling mechanism is activated by the foreshortening but there is no corresponding change in the vertical dimension. Consequently, the constant vertical dimension must be scaled as a gradually increasing size, a perceptual quality called stretching. To put it another way, the pattern on the left is the stimulus for perceived stretching.
Reports of perceived stretching are frequently taken as implying that the unity constraint functioned but the rigidity constraint and depth scaling mechanism did not. It should now be clear that this is not the interpretation proposed here. Within this framework, the operation of the rigidity constraint and depth scaling mechanism is manifested in all aspects of the perception of the quadrilateral, but it does not necessarily result in the perception of a rigid surface. When the figure appears to move in depth, it appears to stretch precisely because the proximal change in the pattern does not correspond to the changes in the two meridians required by the depth scaling mechanism to maintain perceived rigid-body motion in depth within the scale. Indeed, Hershenson(52-53) used precisely this combination of mechanisms, the rigidity constraint and the depth scaling mechanism, to explain anomalies of size-distance perception such as micropsia, the moon illusion, and the spiral aftereffect. In these cases, however, the illusions occur when proximal size is unchanging while the perceived depth plane changes due to other factors.
DISCUSSION
A framework was proposed for analyzing the perception of motion in depth produced by simple proximal motion patterns of two to four points. The separation between two proximal points and the orientation of the axis connecting them may change or remain fixed over the course of a motion pattern. The combinations of these events yielded four types of motion patterns: parallel, circular, perspective, and parallax patterns, the simplest relational patterns in the proximal stimulus. These elementary proximal motion patterns initiate automatic processing mechanisms, the unity and rigidity constraints. The unity constraint was defined as activity of the visual system that treats pairs of points as connected. It is manifested in reports of subjective contours connecting pairs of moving points. The rigidity constraint was defined as the activity of the visual system that treats pairs of points as rigidly connected. It is manifested in reports of apparently rigid connections between pairs of points. When the constraints are activated by perspective or parallax patterns, the rigid contour that appears to connect the points also appears to move in depth. A depth scaling mechanism governs the degree to which the objects move in depth in order to maintain the perceived rigiditythe size and shape constancy of the object. When perceptual constancy is defined as the perception of rigidity, it is dissociated from judgments of the metric size, shape, and distance (position in depth) of objects.
When the analysis was extended to three- and four-point proximal motion patterns, most of the patterns resulted in the perception of rigid surfaces moving in space in various but predictable ways. However, some configurations produced perceptions that had new kinds of emergent qualities such as shrinking, stretching, bending, and folding. For example, the analysis demonstrated how perceived shrinking or enlarging could be understood within the explanatory framework (basic stimulus patterns, constraints, and depth scaling mechanism) as consequences of a specific configurational property, namely the position of the point of convergence of the motion. A different kind of configurational analysis showed how proximal foreshortening and compression are related to the perception of stretching. Thus, the analysis of larger configurations underscored an important unifying aspect of the proposed explanation: despite the fact that the rigidity constraint is always activated, the object that appears to be moving in depth may not appear to be rigid.
The analysis and supporting evidence also made manifest the contingent relationship between perceived motion in depth and a scaling mechanism necessary to maintain perceived rigidity. This relationship explained why some proximal patterns appeared to be shrinking objects in a fixed depth plane, some appeared to be rigid (constant-sized) objects moving in depth, and some appeared to stretch. The patterns that appeared to shrink moved toward a point on the axis connecting two of the points. Patterns that appeared to stretch had one side that appeared to be anchored in a single depth plane and an opposite side that appeared to be moving in depth. However, the separation between these sides (altitude) did not decrease with increases in the apparent depth of the receding side (compression). Consequently, the scaling mechanism produces the perception of an object that stretches as it moves in depth. This kind of analysis has been carried further in the context of anomalous size-distance perceptions such as micropsia, the moon illusion, and the spiral aftereffect(52-53). In these situations, the object appears to change position in depth even though the proximal pattern is unchanging. However, this time, scaling weights are applied that result in an increase in perceived size with a decrease in perceived distance and vice versa.
Invoking the concept of automatic constraints has two distinct advantages over other types of explanations. First, it is more parsimoniousa single system accounts for the monocular perception of rigid and nonrigid objects and their motion in space. It is not necessary to invoke a decision maker (executive) because the same mechanism operates regardless of input(28). Second, attributing perceived rigidity to the operation of a constraint permits the separation of perceived rigidity from perceived metric sizethe former is an outcome of an automatic mechanism whereas the latter is related to an acquired scale of perceived space(25). Thus, cognitive factors that determine the scale of space affect perceived metric size but not perceived rigidity.
In conclusion, it may be suggested that the usual formulation of the KDE may have the problem backwards. In the traditional view, three-dimensional structure is "inferred" from moving two-dimensional proximal patterns. Consequently, the problem has sometimes been described as one of inferring "structure-from-motion." In contrast, the analysis presented here treated perceived rigidity (structure) as a consequence of a processing constraint representing automatic activity of the visual system. If the constraint produces the perceived structure, what produces the perception of motion in depth? It must be a consequence of the activity of the constraints when specific proximal patterns (perspective or parallax patterns) are present in the proximal stimulus. In this sequence of events, the KDE may better be described as an example of "motion-from-structure."
REFERENCES
1. Gibson JJ. The perception of the visual world. Boston: Houghton Mifflin, 1950.
2. Hildreth EC. The measurement of visual motion. Cambridge, MA: MIT Press, 1982.
3. Koenderink JJ. Optic flow. Vision Res 1986;26:161-80.
4. Koenderink JJ, van Doorn AJ. Invariant properties of the motion parallax field due to movement of rigid bodies relative to an observer. Opt Acta 1975;22:773-91.
5. Braunstein ML, Andersen GJ. A counterexample to the rigidity assumption in the visual perception of structure from motion. Perception 1984;13:213-7.
6. Caudek C, Proffitt DR. Depth perception in motion parallax and stereokinesis. J Exp Psychol Hum Percept Perform 1993;19:32-47.
7. Cutting JE, Proffitt DR. The minimum principle and the perception of absolute, common, and relative motions. Cognit Psychol 1982;14:211-46.
8. Proffitt DR, Rock I, Hecht H, Schubert J. The stereokinetic effect and its relations to the kinetic depth effect. J Exp Psychol Hum Percept Perform 1992;18:3-21.
9. Todd JT. Visual information about rigid and non-rigid motion: A geometrical analysis. J Exp Psychol Hum Percept Perform 1982;8:238-52.
10. Börjesson E, von Hofsten C. Spatial determinants of depth perception in two-dot motion patterns. Percept Psychophys 1972;11:263-8.
11. Johansson G. Spatial constancy and motion in visual perception. In: Epstein W, editor, Stability and constancy in visual perception: Mechanisms and processes New York: Wiley; 1977, p.375-419.
12. Johansson G. About the geometry underlying spontaneous visual decoding of the optical message. In: Leeuwenberg ELJ, Buffart HFJ, editors, Formal theories of visual perception. New York: Wiley; 1978, p.265-76.
13. Johansson G, von Hofsten C, Jansson G. Event perception. Annu Rev Psychol 1980;31:27-63.
14. Börjesson E, von Hofsten C. Visual perception of motion in depth: Application of a vector analysis to three-dot motion patterns. Percept Psychophys 1973;13:169-79.
15. Börjesson E, von Hofsten C. A vector model for perceived object rotation and translation in space. Psychol Res 1975;38:209-30.
16. Börjesson E, Ahlström U. Motion structure in five-dot patterns as a determinant of perceptual grouping. Percept Psychophys 1993;53:2-12.
17. Johansson G. Configurations in event perception. Uppsala: Almqvist & Wiksells, 1950.
18. Johansson G. Rigidity, stability, and motion in space perception. Acta Psychol 1958;14:359-70.
19. Johansson G. Perception of motion and changing form. Scand J Psychol 1964;5:181-208.
20. Johansson G. On theories for visual space perception. A letter to Gibson. Scand J Psychol 1970;11:67-74.
21. Johansson G. Visual perception of biological motion and a model for its analysis. Percept Psychophys 1973;14:201-11.
22. Johansson G. Projective transformations as determining visual space perception. In: MacLeod RB, Pick Jr. HL, editors, Perception: Essays in honor of James J. Gibson. Ithaca: Cornell University Press; 1974a, p.111-35.
23. Johansson G. Vector analysis in visual perception of rolling motion: A quantitative approach. Psychol Forschung 1974b;36:311-9.
24. Ullman S. The interpretation of structure from motion. Proc R Soc Lond B 1979;203:405-26.
25. Hershenson M. Size-distance invariance: Kinetic invariance is different from static invariance. Percept Psychophys 1992a;51:541-8.
26. Carlton EH, Shepard RN. Psychologically simple motions as geodesic paths. I. Asymmetric objects. J Math Psychol 1990a;34:127-88.
27. Carlton EH, Shepard RN. Psychologically simple motions as geodesic paths. II. Symmetric objects. J Math Psychol 1990b;34:189-228.
28. Hershenson M. The perception of shrinking in apparent motion. Percept Psychophys 1992b;52:671-5.
29. Hershenson M. Structural constraints: Further evidence from apparent motion in depth. Perception 1993;22:323-34.
30. Jansson G, Johansson G. Visual perception of bending motion. Perception 1973;2:321-6.
31. Wallach H, O'Connell DN. The kinetic depth effect. J Exp Psychol 1953;45: 205-17.
32. Regan D. Visual processing of four kinds of relative motion. Vision Res 1986;26:127-45.
33. Tanaka K, Saito H. Analysis of motion of the visual field by direction, expansion/contraction and rotation cells clustered in the dorsal part of the medial superior temporal area of the Macaque monkey. J Neurophysiol 1989;62:626-41.
34. Bell HH, Lappin JS. The detection of rotation in random-dot patterns. Percept Psychophys 1979;26:415-7.
35. Regan D, Beverley KI. Visual response to vorticity and the neural analysis of optic flow. J Opt Soc Am 1985;2:280-3.
36. Werkhoven P, Koenderink JJ. Visual processing of rotary motion. Percept Psychophys 1991;49:73-82.
37. Börjesson E, von Hofsten C. Effects of different motion characteristics on perceived motion in depth. Scand J Psychol 1977;18:203-8.
38. Johansson G, Jansson G. Perceived rotary motion from changes in a straight line. Percept Psychophys 1968;4:165-70.
39. Swanston MT, Gogel WC. Perceived size and motion in depth from optical expansion. Percept Psychophys 1986;39:309-26.
40. Shepard RN. Psychophysical complementarity. In: Kubovy M, Pomerantz JR, editors, Perceptual organization. Hillsdale, NJ: Erlbaum, 1981.
41. Shepard RN. Ecological constraints on internal representation: Resonant kinematics of perceiving, imagining, thinking, and dreaming. Psychol Rev 1984; 91:417-47.
42. Shepard RN, Cooper LA. Mental images and their transformations. Cambridge: MIT Press, 1982.
43. Hochberg J. Visual perception of real and represented objects and events. In: Smelser NT, Gerstein DR, editors, Behavioral and social sciences. Washington, DC: National Academy Press; 1985, p.249-98.
44. Ullman S. The interpretation of visual motion. Cambridge: MIT Press, 1978.
45. Braunstein ML. Depth perception through motion. New York: Academic Press, 1976.
46. Ittelson WH. Visual space perception. New York: Springer, 1960.
47. Restle F. Coding theory and the perception of motion configurations. Psychol Rev 1979;86:1-24.
48. Rock I. The logic of perception. Cambridge: MIT Press, 1983.
49. Loomis JM, Eby DW. Perceiving structure from motion: Failure of shape constancy. In: Second International Conference on Computer Vision. Los Angeles: IEEE Computing Society Press; 1988, p.383-91.
50. Lappin JS, Ahlström UB. On the scaling of visual space from motion – in response to Pizlo and Salach-Golyska. Percept Psychophys 1994;55:235-42.
51. Lappin JS, Love SR. Planar motion permits perception of metric structure in stereopsis. Percept Psychophys 1992;551:86-102.
52. Hershenson M. Moon illusion and spiral aftereffect: Illusions due to the loom-zoom system? J Exp Psychol Gen 1982;111:423-40.
53. Hershenson M. Moon illusion as anomaly. In: Hershenson M, editor, The moon illusion. Hillsdale: Erlbaum; 1989, p.123-45.
54. Ikeda S. The apparent distance in darkness: the relations of apparent distance to stimulus size. Jpn J Psychol 1960;30:339-49.
55. Ittelson WH. The constancies in perceptual theory. Psychol Rev 1951;58:285-94.
56. Noguchi K, Taya K. A neglected problem: Kinetic size constancy. Acta Psychol 1981;49:187-94.
57. Schiff W. Perception of impending collision: A study of visually directed avoidant behavior. Psychol Monographs 1969;79:Whole 604.
58. Hatfield G, Epstein W. The status of the minimum principle in the theoretical analysis of visual perception. Psychol Bull 1985;97:155-86.
Correspondence to
Maurice Hershenson
Department of Psychology, Brandeis University, Waltham, MA 02254
E-mail: [email protected]
phone: (617) 736-3267
1 Orientation as a dimension is not the same as describing retinal (proximal) position using polar coordinates centered on the fovea because, as used here, orientation does not imply an origin. Nevertheless, the quantitative aspect is also of interest. For example, orientation may have meaning if the horizontal or "level" (0-deg) meridian is related to the perceived horizon. This meaning makes especially good sense for binocular vision because it can be related to horizontal retinal disparities
2 Motion patterns in figures are illustrated in a single direction. It is assumed that the reciprocal proximal pattern results in the perception of motion in the opposite direction.
3 To simplify describing some of the data reported below, small numbers of translation/rotation responses are combined with simple translation or rotation responses.
4 An asymmetrical size-change pattern is produced by a combination of size-change and linear motions.