ABSTRACT

In contrast to the CIE (Commission Internationale de l'Eclairage) colorimetric systems in which colors are specified on the basis of spectrum of light, a system for surface color is displayed by the standard chips. According to the principle by which the standard chips are selected and arranged, we have many different systems. Three representative systems are examined, Munsell, OSA-UCS (Optical Society of America-Uniform Color Scale), and NCA (Natural Color System) of Sweden. Each is a systematization of human cognition of colors, and how we see the difference between two chips j and k plays a different role in each spatial representation. On the basis of observers' assessments, the perceptual difference is scaled as d jk, a numerical value. The structure of each system is quantitatively examined by checking the behavior of d jk. This article is a review of the author's studies in this line.

Keywords: Color vision; colorimetry; psychophysical scaling; multi-dimensional representation

RESUMO

Em oposição aos sistemas colorimétricos da CIE (Commission Internationelle d'Éclairage), nos quais as cores são especificadas com base no espectro luminoso, apresenta-se um sistema para cor de superfícies que emprega os discos padrões. De acordo com o princípio pelo qual os discos padrões são selecionados e arranjados, obtém-se vários sistemas diferentes. Três sistemas representativos foram examinados, o de Munsell, o da Optical Society of America - Uniform Color Scale, e o Natural Color System da Suécia. Cada sistematização da cognição humana de cores e de como discriminamos a diferença entre dois dados discos, j e k, desempenham papéis diferentes em cada representação espacial. Baseado nas respostas dos observadores, a diferença perceptual foi representada por um valor numérico djk. A estrutura de cada sistema foi examinado quantitativamente pela observação do comportamento de djk. Este artigo é uma revisão dos estudos do autor seguindo esta linha.

Descritores: Visão de Cores; Colorimetria; Escalas Psicofísicas; Representação Multidimensional

---

 

 

VISUAL SPACE AND COLOR

Unlike sensory experience in other modalities, what one sees is a spatially structured scene. Let us call it visual space. This is the end product of the processes that starts from the retinal image of the physical space. If the entire retina is exposed to homogeneous light of a sufficient low intensity, the visual space is not structured and one feels as if being surrounded by fog of light. This is called Ganzfeld experience⁽¹⁾. When retina is stimulated by light of a structured pattern, one we sees a scene extending in the three directions from the self. The self is the percept of the physical body and it acts as the origin of visual space. Hence, the physiological processes underlying visual space are connected to the excitation that stems from proprioceptive stimulation. What one sees around the self is due to multiple glances. Nevertheless, the visual space is stable and its structure can be discussed in its own right without touching upon the underlying physiological basis^(2-3).

One always sees a percept at the end of line of sight and the percept always appears at a finite distance from the self. In other words, neither nothing nor infinity can be a percept. There exists a terra incognita between a percept and self, but the percept itself cannot be void. Indoors, the percept may be a person or the wall and outdoors, the percept may be a tree or the sky. An object that is beyond a certain distance from the body in the physical space, e.g., a flying plane or a constellation of stars, is perceived at a finite distance from the self. How far it appears depends upon the total configuration of stimuli in the physical space⁽⁴⁾. All percepts at the end of sight have color, achromatic or chromatic. Otherwise, one cannot see them. The sky may be blue when it is fine and gray when it is cloudy. In the present article, I am going to discuss color that appears in visual space as a perceptual property of a percept. The number of colors we can name is limited, but the number of colors we can discriminate one from another is extremely large, possibly seven million. Hence, to identify each color, we have a few options than representing colors as points in a space. According to the principle by which colors are allocated, we have various color spaces. Color can appear in various modes. When we observe light coming through a small aperture, the aperture appears being filled by a color. This appearance is called aperture mode. The color appears floating in the air and we feel as if our finger will penetrate into the color. The color of a perceived object appears in a different way. We feel we can touch the color. This appearance is called surface or object mode. The purpose of this article is to discuss three kinds of system that specifies surface colors.

 

COLOR SPACES

The correspondence between color and radiant power spectrum P(l) of light is one to (indefinitely) many. There are many different spectra that yield the same color. The Commission Internationale de l'Eclairage (CIE) defined such a 3-D space that all these spectra P(l) are represented by a point P(X, Y, Z). Hence, P(X, Y, Z) and color have one-to-one correspondence for the standard observer. This is called the CIE Colorimetric System and has been established on the basis of the following color matching experiment. In a small aperture, a standard stimulus Q₀ is presented on its half field and three primary lights Q_m are presented in the other half field. The observer adjusts the intensity of each Q_m until the appearance of the additive mixture becomes identical with the appearance of Q₀. In the basic experiments, Q_m are three monochromatic lights, {R(e.g., 600nm), G(e.g., 530nm) and B(e.g., 460nm)}, and Q₀ is a spectrum yielding an achromatic color (W) or a monochromatic light of l of a given intensity. In this way, (R_W, G_W, B_W)and (R_l, G_l, B_l)are experimentally determined. A monochromatic light of l yields the most saturated appearance of that hue. Any non-monochromatic Q₀ yielding a less saturated appearance can be matched by a mixture of an appropriate monochromatic light l and an achromatic light W. Because of Grassman's law, (R, G, B) of this Q₀ can be calculated from (R_l, G_l, B_l) and (R_W, G_W, B _W). Thus any color stimulus is specified as a point (R, G, B), and it has one-to-one correspondence with a color. For some Q₀,one of Q_m is negative, e.g., for Q₀ (l=500nm), R_l < 0. The appearance of Q₀ cannot be matched by any mixture of R, G, B, but the mixture (500nm + R_l) is matched by the mixture of G_l and B_l. As a matter of course, there are individual differences in matching, and CIE defined standard matching results. Namely, this is a system that uniquely specifies colors of aperture mode for the standard observer. In order to avoid negative values and for some other reasons, CIE transformed the results with the set of primary stimuli {R, G, B} to the results that would be obtained with another set of primaries {X, Y, Z}. These three can not be realized by actual color stimuli and hence representing a color in terms of (X Y Z) is a mathematically derived system. The transformation is based on the fact that human visual process behaves as a linear system with regard to color matching. This XYZ system can be further transformed to a system that represents a color stimulus as a point (x, y, Y). The variable Y is given by the integration of the luminous efficiency function V(l) and specifies brightness of the color and the plane of (x, y½Y) represents hue and saturation of that color. This plane is called a chromaticity diagram.

Once a spectrum P(l) is given, we have a procedure to calculate (x, y, Y). The color of aperture mode produced by this light is uniquely specified by a point P(x, y, Y), and this color space provides us with the foundation for modern color reproduction technology. The spectrum P_T(l) of light coming from image of an object on TV monitor is different from the spectrum P_O(l) of the light reflected from the original object. When converted to P_T (x, y, Y) and P_O(x, y, Y), the two points should be close. For any two spectra P_A(l) and P_B(l), we can define P_A (x_A, y_A, Y_A) and P_B (x_B, y_B, Y_B) that are separated by a distance d_AB in the (x, y, Y) space. However, the correspondence between d_AB and the perceptual relationship between colors A and B is not specified. In this sense, no metric is defined in the space. Between two colors, we feel various degrees of similarity or difference. Around a point P₀(x₀, y₀, Y₀), we can define a region W comprising all (x, y, Y) that yield colors indistinguishable from the color P₀. The boundary of W divides color stimuli into two groups, indiscriminable and discriminable from P₀(x₀, y₀, Y₀), according to a certain criterion. A point P on the boundary of W is called jnd (just-noticeable-difference) of P₀(x₀, y₀, Y₀) in that direction. MacAdam⁽⁵⁾, Brown and MacAdam⁽⁶⁾ showed that W is approximated by an ellipsoid. Let us call W a discrimination ellipsoid in the (x, y, Y) space or a discrimination ellipse in a chromaticity diagram (x, y½Y) when Y is held constant. That W is not a circle means that jnd is not represented by same distance from P₀(x₀, y₀, Y₀) according to the direction. Furthermore, W considerably changes its size and form according to the position of P₀(x₀, y₀, Y₀) in this space, which means this space is not homogeneous with regard to jnd.

Light yields a color of aperture mode only when its retinal image is a small area surrounded by the uniform background of intensity lower than the light. One exception is the appearance of the large blue sky. It is of aperture mode. The retinal image of a physical surface gives rise to a surface color when it appears as a percept in the structured visual space. Brightness of an aperture color changes from dark to bright whereas lightness of a surface color changes from black to white. In order to appear as black, it is necessary to have a structured surround. When a TV screen is homogeneous without any picture, it can be dark gray but not black. When we see a pattern, its part can appear real black. The light yielding a brown surface appears dark red when observed through a tube. In order to be brown, blackness must be induced from the surround. Specification of surface colors can be made in two ways. One way is through the colorimetric analysis of light P(l) coming from a physical surface; P(l) = R(l)E(l), where R(l) is the spectral reflectance of surface and E(l) is the spectrum of illumination. Usually (X, Y, Z) is defined under the standard illumination, CIE C or D65. In this specification, (X, Y, Z) mean normalized values with regard to the luminance of illumination. The other way is through visual comparison of a surface with a standard frame of reference for surface mode colors under the standard observing condition. Then, the color of surface is denoted by coordinate values of the reference frame. Standard frames of reference for this purpose are often called color order systems. A color order system is a set of standard color chips that are arranged in accordance with a specified scheme. The standard chips are specified in terms of (x, y, Y) and manufactured so as to satisfy that specification. We have a number of color order systems and three representative systems based on different principles will be discussed below.

 

MUNSELL COLOR SOLID

Its construction

This system was originally defined by A.H.Munsell, an artist and educator in Boston. The first book, A Color Notation, was published in 1905. This is "an exeprimental system built up with the aid of a new photometer, Maxwell disks, and the trained capacity of the painter"⁽⁷⁾. The basic principle is to arrange standard color chips according to cylindrical coordinates. This is called Munsell color solid (Fig. 1). The virtical axis in the center represents lightness (called Value V), polar angle and polar distance represent Hue H and saturation (called Chroma C). In each coordinate, adjacent standard chips are supposed to differ perceptually with a constant step. The Optical Society of America (OSA) established in 1937 a committee to examine the color spacing in the Book of Color (1929). The assessment methods used by the committee are described in Newhall^(8-10). What we use today is the Renotation Munsell based on the study of this committee⁽¹¹⁾. Lightness V varies from 0 (ideal black) to 10 (ideal white). The hue circle at a given V is divided into 10 sectors of the same size, 5 principal hues [red (R), yellow (Y), green (G), blue (B) and purple (P)] and 5 intermediate hues such as yellowish red (orange) YR, bluish green BG, etc. Each of these 10 sectors is subdivided into 10 steps, 0 to 10, where 5 is given to the most representative color of the sector. For instance, 5R means pure red and 10R (= 0YR) means the hue at the border between R and YR. Chroma C varies from 0 (gray at V) to a most saturated color of that H at V. How far C extends depends upon H and V. For instance, for 5R at 5V, most books give the chips, 2C, 4C,..., 12C. By comparing a sample to the Munsell solid under a standard illumination, we can assign it a set of values (H, V/C). Often, visual interpolation becomes necessary. In each attribute, standard color chips constitute a series of equal appearing intervals, which is helpful in making interpolation easier. However, no attempt has been made to equate step sizes between different attributes. From experience, color practitioners know that a difference of 1V interval roughly corresponds to a difference of 2C interval.

 

 

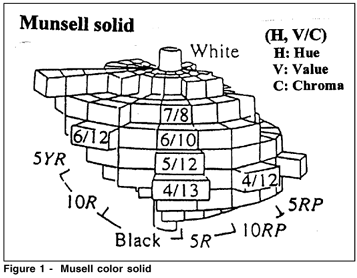
It is rare to see two aperture colors at a time. In Munsell solid, on the other hand, we can see the 3-D display as a whole and perceive supra-threshold relationships between standard chips. Let us denote by d_jk the difference we see between (H_j, V_j/C_j) and (H_k, V_k/C_k). When two are neighboring chips in an attribute, such as (H, V/C_j) and (H, V/C_k) where C_k = C_j ± 2, this uni-attribute difference d_jk is a constant by definition for any C_j. It is not in the logic of construction, however, what d_jk is represented by the distance between two points (H_j, V_j/C_j) and (H_k, V_k/C_k) in the display, when two are different in more than one attribute or in more than one step in an attribute.

Psychophysical scaling of d

The difference d_jk is felt something like a magnitude and can be regarded as a latent variable in the sense that no other person than the observer can experience it However, it is possible to ask the observer to assess its size and to define an overt variable d_jk that is supposed to represent d_jk. Let us call d_jk a scale value of d_jk, and two methods of scaling are explained below. One is ratio assessment of d and the other is to match d to a lightness difference between two grays.

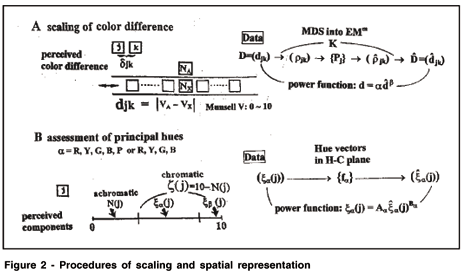
In the former, for a triplet of color stimuli (j, k, l), the observer is asked to assess the subjective ratio between two perceptual differences d_ij and d_ik. The observer can assign any positive value r_i.jk that is felt appropriate to represent d_ij/d_ik. The assessment is consistent in the sense that r_{i..l k} coincides well with r_i.jl × r_i.jk. Once a matrix (r_i.jk), i, j, k = 1, 2,....., N, is obtained, it is possible to define a matrix D = (d_jk), N × N, where d_jk = d_kl and d_jj = 0. The scaled value d_jk is defined with a common (arbitrary) unit, and d_ij/d_ik closely reproduces the data r_i.jk^(12-13). The second method makes the use of the fact that Munsell Value Scale varying from the ideal black V=0 to the ideal white V=10 with perceptually equal steps. The Munsell grays are a most well established series of equal-appearing intervals and standard chips with a small step size, e.g., 0.25V, are available. A pair of colors (j, k) is presented to the observer at a time. Using a slide rule type apparatus in which a series of Munsell grays N_I, I = 1, 2,......, on the moving part and a fixed gray N_A is on the fixed part The task of observer is to select such a gray N_X on the moving part that the lightness difference between N_A and N_X matches in size with the color difference d_jk (Fig. 2A). Then d_jk..t = |V_A - V_X| is a scale value of d_jk on an occasion t and d_jk..t is given with unit of V. The observer is encouraged to interpolate, if necessary, to respond such that N_X is between N_I and N_I+1. The procedure is repeated with different N_A. The variation of d_jk..t by one observer is between 0.25V to 0.50V. Usually results are obtained from 5 observers and the grandmean is defined as the scale value d_jk. In this article, the results obtained from the data D = (d_jk) by the second method will be discussed.

 

 

The range in which d can be well defined as d is limited. When two colors, (j, k), are too different, e.g., (a highly saturated red and a highly saturated green), the two are qualitatively different and d is not felt as magnitude. Furthermore, it is not likely, if d_ik is beyond a certain level, that we can have d's that meet the additivity condition, d_ik = d_ij + d_jk for triplets that are represented by collinear points (P_i, P_j, P_k) in this order in a color space. Hence, pairs (j, k) to be assessed are limited within the range in which size of d is intuitively clear to the observers. Namely d_jk is at most 3.5V and D= (d_jk), N ' N, is incomplete in the sense that it has a number of undefined vacant cells.

Multidimensional representation of Munsell solid

From a data matrix D = (d_jk), N × N, with N Munsell colors, we can construct a configuration of N points {P_j} in an m-dimensional space R^m such that inter-point distances _jk reproduce data d_jk. This is a generalized Multidimensional Scaling (MDS) and its steps are given in Fig. 2A. In an ordinary MDS, {P_j} is constructed in E^m, an m-dimensional Euclidean space. In the procedure in Fig. 2A, colors are embedded as {P_j} in R^m, a Riemannian space of constant Gaussian curvature K. According to whether K is positive, or 0, or negative, R^m is elliptic or Euclidean (E^m), or hyperbolic. These spaces are visualized in a 3-D Euclidean map (Poincaré's model) in different ways according to K. The configuration {P_j} is defined in the Euclidean map, EM. In Fig. 2A, 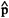_jk means the distance in the Euclidean map between P_j and P_k, and _jk means the length of corresponding geodesic in the Munsell solid. How r and d o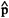r and , are related is completely determined by the parameter K only. If K= 0, then d = r and 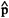= , and it is not necessary to consider the Euclidean map. It is assumed that a power relationship holds between d and , d = a^b. The parameter a only depends upon the units by which d and are defined and has no substantive meaning. On the hand, the exponent b (> 0) determines the shape of curve when d is plotted against . It is concave upwards when b > 1 and convex upwards when b < 1. If b = 1, d is proportional to and the curve is a straight line passing through the origin. For a given D = (d_jk), the program determines optimum values of m (dimensionality), the sign and value of K, the configuration {P_j}, and the values of a and b.

The experimental studies started from 1960 (see Table 1⁽¹³⁾). In the beginning, the number of colors, N, was limited because of the capacity of computer, and {P_j} was constructed in Euclidean space E only. After 1980, I could obtain results with N = 120, 278, etc. When {P_j} was constructed in R^m, the following results were obtained. The dimensionality m turned out to be 3, K is not far apart from 0, and b is close to 1.0. The concentric circle like pattern inside the outmost circle in Fig. 3A is an example of {P_j} that has been obtained under the constraint of K being 0. Let us call it {P_j} in E³. Since the axis representing the V-axis turned out orthogonal to the plane representing H and C, all points are vertically projected on the H-C plane at an arbitrary level of V₀. If a positive value of K is taken, equi-chroma circles of {P_j} with this K are slightly more equally separated from C to C+2⁽¹³⁾. However, the difference between {P_j} with K > 0 and {P_j} in E³ is small, and hence the discussion will be limited to the latter only. The Munsell solid is displayed by standard chips in the physical space E³ and it is important to understand what is represented by inter-point distances in this display.

 

 

Fig. 3B shows an example of plotting of d against , inter-point distances in {P_j} measured by an arbitrary unit. Because b is almost 1.0, points scatter around the line passing through the origin. The slope depends upon the unit of . We can re-scale the abscissa so as to make the slope 45 degree and re-denote it as . The degree of scatter of points around this is given by RMS (root-mean-squares) of (d - ), where M is the number of d's.

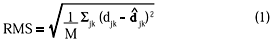
Values of RMS were 0.20 ~ 0.26V when {P_j} was constructed from a data matrix D = (d_jk) in E³. This value of RMS is only about 2 times of the jnd threshold of lightness discrimination in the Munsell gray series. Hence, we can conclude that Munsell chips can be embedded as {P_j} in E³ with a sufficient degree of reproducibility. This assertion does not imply that the entire Munsell solid is of Euclidean property, because comparisons between d and are limited in the range of smaller than 3.5V. The space implied by E³ is a 3-dimensional manifold with locally Euclidean metric. The configuration {P_j} in E³ represents the basic structure of the Munsell solid. Fig. 3A is {P_j} based on two sets of D = (d_jk), in each d_jk are mean results of 5 observers. It is known that even if {P_j}_i are individually constructed from D_i = (d_jk)_i of observers i of normal color vision, these {P_j}_i exhibit essentially the same structure⁽¹³⁾.

Chips P_j(H, V_j/C_j) of the same H form a regular lattice having V and C as two orthogonal coordinates, and 1V step corresponds to 2.3 C step on the average. This fact is in agreement with the intuition of color practitioners stated in 3.1. Chips P_j(H_j, V/C_j) of the same V forms a concentric circle type configuration in a flat plane that is ordered according to V. The Munsell V is defined in terms of Y of the reflected light. Often the tendency is pointed out that color of a given Y tends to appear brighter or lighter when its saturation is high (Helmholtz-Kohlrausch effect). If this effect is apparent with {P_j}, each plane of constant V should be curved upwards at its rim like a saucer. Presumably, points P_j are not dense enough to make this effect explicit. The form of {P_j} in the H-C plane is topologically in agreement with the Munsell notation of H and C. Many quantitative deviations from Munsell notation are noticeable, however. The program constructs {P_j} so as to minimize RMS (1) and some ad hoc distortions for this purpose only may have been introduced to {P_j}. However, there are some systematic deviations that cannot be regarded as artifacts. One is the anormaly of H spacing in the region from B to P. Munsell defined {R,Y,G,B, P} as 5 principal hues and divided H-circle into 5 equal sectors of 72 degree. The most representative hue in each sector is denoted such as 5R, 5Y, etc. In {P_j}, 5G and 5B are separated by about 30 degree only. It is not a surprise that the a priori defined structure of hue circle is not completely supported by empirical observation.

A color appears reddish, yellowish etc. Its saturation changes according to the degree of achromaticness involved. From assessment of these perceptual components, a set of unit vectors {f_a} can be defined in the same space in which {P_j} has been constructed. The procedure is described in Fig. 2B. A color j is presented one at a time. The task of observer is to divide a line segment of length 10 into parts N(j) and x_a(j) in accordance with the degree of grayness and principal hue component a. The grayness and hue components that the observer sees in a color j are latent variables and lengths, N(j) and x_a(j), are their overt variables. Usually, two hue components are sufficient to describe the appearance of a color j. If it is saturated orange, N(j) is close to 0 and only x_R(j) and x_Y(j) are positive. For a less saturated color j, N(j) is large and Sx_a(j) is small. In this case, the chromatic impression is so obscure for some observers that they assign positive values to three x_a(j). Hue vectors {f_a} can be defined individually from individual data matrix {x_a(j)}_i. An example of {f_a}_i of 5 observers is shown along the outmost circle in Fig. 3A. Five bundles inside the circle are individual f_{a i} when 5 hue names were used and four bundles outside the circle are individual f_ai when 4 opponent hue names were used. According to his diary of April 13, 1900, Munsell had the idea of using the five hues as the cornerstones of the hue circle. He referred to the rainbow as an example in nature⁽¹²⁾. It is an interesting question how many hues human sees in the rainbow. The observers do not have any difficulty in specifying Munsell chips in terms of the four hue names. Adding P helps only to reduce the range of other bundles, and the bundle P is almost in the middle of bundles of R and B. In this sense, P is redundant, and hereafter discussion will be limited to four principal hues, and four vectors based on averaged data {x_a(j)} are denoted as {f_a}, a = R, Y, G, and B. Each f_a goes through the middle of the respective bundle outside of the circle in Fig. 3A. How f_a are defined from the data {x_a(j)} is explained with regard to Fig. 4A.

 

 

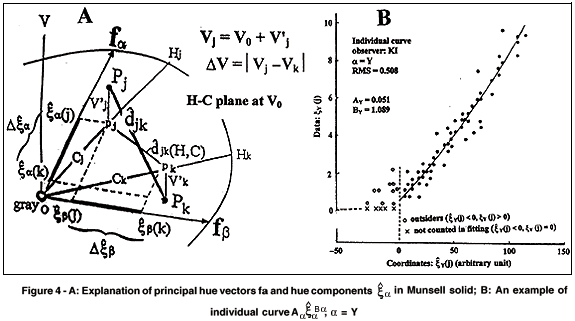
The set {f_a} is defined in the H-C plane at an arbitrary level of V, V₀. All point P_j are projected along V-axis on this plane as p_j. Chroma C and Value Vof a color j are respectively represented by the vector C_j stretching from the origin to p_j and by V₀ plus the distance to P_j from this plane. The coordinate of P_j on f_a is denoted as 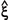_a(j). Since f_a and f_b are not orthogonal, how to define the coordinate is not unique, and _a(j) is defined as shown in Fig. 4A. This is the contravariant component of C_j in the direction of f_a. The reason why this definition was adopted was explained before^(14-16). When p_j is not in the sector spanned by f_a and f_b, _a(j) < 0. It is assumed that, when data x_a(j) are plotted against 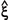_a(j), points scatter around a power function A_a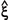a^Ba for P_j in which x_a(j) > 0 and 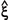_a(j) > 0. It is also assumed that x_a(j) = 0 for P_j in which 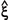_a(j) < 0. But, these points were not included in the curve fitting. Anomalous pairs (x_a(j) > 0 and 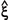_a(j) < 0) are regarded as outsiders. From the data matrix {x_a(j)}, {f_a} and parameters A_a and B_a were defined so as to make the number of outsiders smallest and the scatter of points around A_{a 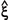a}^Ba as small as possible. The possible range of x_a is between 0 and 10, and the degree of scatter is given by RMS of (x_a(j) - A_{a 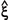a} ^Ba). Fig. 4B shows an example of plotting x_aY(j) against 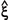_Y (j) for an observer. The values of A_a and B_a changes according not only to the principal hue a but also to V_j of color j (Table III(16)).

The anomalous H-spacing in {P_j} stated in 3.3 that colors of 5B are located too close to colors of 5G (about 30 degree) in Fig. 3A suggests two possibilities. One is that, among the four cornerstones, B and G do not look so different as G looks different from Y. The other is that the Munsell notation of 5B is not the pure Blue. At first, I was inclined to the first interpretation. But, now it has become clear that the second interpretation is correct. The real Blue for human eye is not at 5B but close to the hue denoted as 5PB. Other f_a, a = R, Y, G, (and P), are in the direction of colors of 5H_a Munsell notation.

Discrimination ellipsoid of surface color

In the CIE space, points P(x, y, Y) of colors that are indiscriminable from P₀(x₀, y₀, Y₀) forms an ellipsoid W (Section 2). A standard color stimulus Q₀ and a comparison color stimulus Q are presented simultaneously. It is a matter of probability whether Q is discriminated from Q₀ or not. The procedure often used to define W for aperture color is as follows. The observer is asked to adjust Q so that its appearance matches that of Q₀. If the matching is repeated a number of times, P(x, y, Y) of matched Q are distributed around P₀(x₀, y₀, Y₀) and the region comprising these points with a specified probability is defined as W. This called the matching method. In the first experiment of MacAdam⁽⁵⁾ in which Y was held constant, Q was changed along a specified direction w from Q₀ on the chromaticity diagram (x, y|Y) so as to obtain the univariate distribution of matched Qw. Then, such 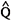_w was determined that Q_w falls between Q₀ and 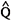_w with a specified probability. Direction w was varied so as 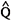_w to surround Q₀. Then, P_w(x_w, y_w,Y) of 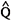_w were found fitted by an ellipse around P₀ (x₀, y₀, Y) in the (x, y|Y) plane. This procedure will be called "guided matching". Guided matching can be performed in the 3-D (x, y, Y) space also. In the other procedure, the observer controlled three knobs to adjust Q in the (x, y, Y) space, which will be called "free matching". The results of free adjustment, P (x, y, Y), follow a 3-D Gaussian distribution having P₀(x₀, y₀, Y₀) as the mean. Its cross-section at a fixed value of probability density forms an ellipsoid W.

We cannot directly apply the matching method when Q₀ and Q are surface color stimuli, e.g., Munsell chips, because Q cannot be continuously changed during the observation. However, it is possible to prepare an appropriate set of Q_i around Q₀, and to ask the observer to make binary judgment about (Q_i, Q₀) whether the two appear the same or not. Let us denote by p(Q_i, Q₀) the proportion that Q_i is judged different from Q₀. Suppose that we have data p(Q_i, Q₀) with Q_i that surround Q₀ with various directions w. Let P(x, y, Y) be the point representing the light reflected from a surface under the standard illumination. Then, a procedure was formulated by which we can define, from p(Q_i, Q₀) observed only with limited number of Q_i's, an ellipsoid W in the CIE space around P₀(x₀, y₀, Y₀) that is equivalent to W that would be obtained by the 3D-guided matching⁽¹⁷⁾. Denote by 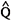_w the color on the boundary of W in the direction w and by P_w(x_w, y_w,Y_w) its position on the chromaticity diagram. Then, we can expect that the surface color (H_w, V_w/C_w) represented by P_w(x_w, y_w,Y_w) is distinguished from (H₀, V₀/C₀) with a specified probability, for any direction w and for any value of the probability. If the data p(Q_i, Q₀) are defined with repeated binary judgments of an observer i, we can define individual W_i. If p(Q_i, Q₀) are group data, one W is defined for the group.

This method was tested with painted surfaces⁽¹⁷⁾ and also with simulated surface colors on a monitor⁽¹⁸⁾. When a color stimulus Q(x, y, Y) is presented on the monitor with the surround darker than it, it appears as an aperture color. When the surround is sufficiently brighter, on the other hand, it looks like a colored patch pasted on the background. Though this color is textureless, it is of surface color mode in other respects. It can be black and brown. With six simulated surface colors Q₀ (A, R, Y, G, B, and Brown respectively represent simulating Munsell gray of V6, 5R5/9, 5Y9/7, 10G6/5, 5PB4/10, and 5YR4/5), W_i were obtained with two observers. Each W_i on the (x, y, Y) space represented data p(Q_i, Q₀) very well, and, except W_i for yellow Y, W_i is similar to W that is expected for the same Q₀ of aperture color mode^(18-19). As to the simulated Y, W_i of both observers were very elongated in the direction of purity. It is yet to be seen whether the same prolongation occurs with W for painted yellow surface when W is constructed from binary judgments. An example⁽¹⁷⁾ suggests it might be the case.

Denote by 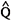_w(H_w, V_w/C_w) the Munsell color at the boundary of the mean ellipsoid of W_i in the direction w from Q₀, then, when w is the direction representing H change, DH = (H_w - H₀) is the jnd differences of H. When w is along the V-axis, DV = (V_w - V₀) is the jnd difference of V. The jnd difference of C, DC, is defined in the same way. If the Munsell space (H, V/C) is perceptually uniform with regard to d at jnd level, each of these D's is expected to be constant for all Q₀. The values of DV(Q₀) are fairly constant and in the order of 0.25V. This value corresponds to RMS (1) between d_jk and _jk in Section 3.3. As to DH(Q₀) and DC(Q₀), the values are less stable⁽¹⁹⁾. It has not been tested what would be if 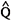_w(H_w, V_w/C_w) are converted to jnd distances D in the configuration {P_j} in E³ that has been constructed from D = (d_jk). At present, {P_j} in E³ is not dense enough for this purpose.

 

COLOR DIFFERENCE PREDICTED BY CPLORC COMPONENT DIFFERENCES

Suppose that {P_j} in Fig. 4A is the configuration directly plotted according to Munsell notation P(H_j V_j/C_j). Then, in order to predict d_jk from DV and _jk (H, C) shown in the figure, we have to define.

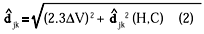
Then, RMS (1) for this _jk is 0.62V (Table II⁽²⁰⁾). Even if _jk (H,C) is multiplied by an appropriate coefficient according to the hue region, RMS (1) is in the order of 0.54V (Table I⁽²¹⁾). Suppose that Fig. 4A is {P_j} in E³ having been constructed from data D = (d_jk). In this case, the vertical axis is not the Munsell V itself, but the axis representing V, and _jk shown in the figure directly gives the value of d_jk, provided _jk < 3.5V. The value of RMS (1) for this _jk is known to be in the order of 0.25V. At present, {P_j} in E³ from data D = (d_jk) does not cover the entire body of Munsell solid. However, it is likely that if D is obtained with sufficient large number of Munsell colors, we can have {P_j} in E³ with locally Euclidean metric that represents any d_jk (< 3.5V) as the inter-point distance _jk with a sufficient accuracy. In so far as supra-threshold differences of medium level are concerned, it is very likely. Furthermore, in the same space, we can have a set of hue vectors {f_a} from which we can predict how the color represented by P_j will appear to human eye. This is a comprehensive spatial systematization of human cognition of surface colors. However, it seems to me not likely that the effectiveness of spatial representation can go beyond this level. In Fig. 4A, geometrically we can relate _jk to DV, Dx_a, and Dx_b. These differences D's are defined in the figure. If this relationship is perceptually meaningful, we can relate d_jk, through _jk, to these component differences DV, Dx_a, and Dx_b. It will provide us with the cognitive basis for why we see the difference d_jk scaled as d_jk between colors j and k that have these component differences. This possibility was tested but the results were not very promising⁽²²⁾. If we want to predict d_jk from component differences, we must combine DV, Dx_a, and Dx_bin a way different from the geometrical relationship holding in Fig. 4A⁽²³⁾. Spatial representations are useful for unique identification of color stimulus, for defining color difference as a distance _jk, and for locating hue vectors f_a. Spaces used for these purposes are means, and we are not necessarily obliged to regard all geometrical relationships in these representations to be perceptually or cognitively meaningful.

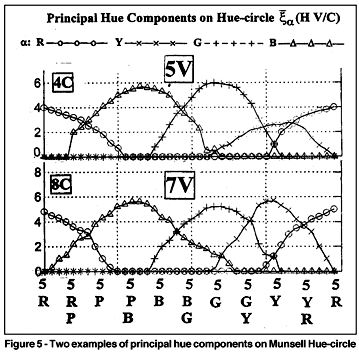
Let us denote by 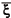_a(H|V/C) the curves obtained by plotting the assessed principal components data {x_a(j)} for Munsell color (H_j, V_j/C_j) against H_j separately according to V_j/C_j. (two examples in Fig. 5).Charts 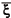_a(H|V/C), a = R, Y, G, B, are prepared for colors 2V - 7V and 2C - 10C and for some colors of 8V and 12C^(22-23). For any surface colors j and k, if their equivalent Munsell notations are known, we can define 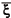_a(H_j, V_j/C_j), 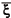_a(H_k, V_k/C_k) and their differences DV, D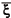_a. Sometimes it becomes necessary to use two or three curves 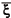_a(H|V/C). To predict dj_k, the scaled color difference between these colors, various functions of (DV, D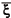_a) were tested. Should a fixed set of coefficient values be used for colors in all hue regions and of all levels of V and C, it was found that

 

 

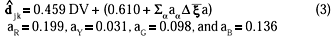
gives the best result. As _jk in (1), 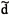_jk is defined with the unit of V, and RMS of (d_jk - 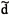_jk) was 0.34V for d_jk in Section 3.2 (M = 899). For colors differing in H and C only (DV = 0), RMS is reduced to 0. 28V. When j and k are identical colors (DV = 0, and all D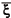_a= 0), 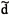_jk = 0.61V. This is not contradictory because is for predicting a clearly perceptible difference between two surface colors when they are not directly juxtaposed. Even if j and k are within a jnd difference, some observer will respond with not-identical grays (V_A, V_X), X ¹ A, and d_jk > 0. This predictor 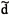_jk is a direct combination of two sets of human assessment, d_jk and x_a(j). No spatial representation of colors is intervened in this procedure.

 

OSA - UCS (OPTICAL SOCIETY OF AMERICA- UNIFORM COLOR SCALES) SYSTEM

The OSA - UCS system is a 3-D display of standard color chips allocated according to the regular rheombohedral lattice structure^(24-26). This is an entirely different principle by which the Munsell system Color chips have been assembled. Except colors on the boundary of solid, each color is surrounded by 12 nearest neighboring colors, all perceptually equally different. In Fig. 6A, 12 colors denoted as (1, 1, 1), (0, -2, 0), etc, are supposed to differ from the color denoted as (0, 0, 0) with the same perceptual size. Namely, all thick lines in Fig. 6A are physically the same length and represent color differences of the same size. The structure is elongated by placing the central point colors at (0, 2, 0) or (-1, 1, 1) etc. Lattice points are specified by the orthogonal coordinate axes L, j, g. and standard chips are placed with the step of 2 in each axis. The vertical axis L represents lightness. In contrast to Munsell V, L is not a function of CIE Y alone. If the solid is sliced at a fixed level of L (horizontal cleavage), standard chips form a rectangular lattice (j, g) where j comes from the French jaune meaning yellow and g means green. For bluish colors j < 0 and for yellowish color j > 0. For reddish colors g < 0 and for greenish color g > 0. Fig. 6B shows a part of the horizontal cleavage at the middle gray L = 0. Standard chips were so selected that all neighboring pairs, (j, g) and (j±2, g) as well as (j, g) and (j, g ±2), appear to have the same size of difference d. In the vertical cleavage in which j + g = a constant, we have a rectangular lattice rotated 45 degree. Fig. 6C shows a part of the vertical cleavage passing through the central gray chip (0, 0, 0). In this cleavage, j + g = 0, and the scale of the abscissa is j (= -g). Four chips being neighbor from (L, j) in oblique directions, (L+1, j-1), (L-1, j +1), (L+1, j+1), and (L-1, j-1) are supposed to differ from (L, j) with the same size d, and this d means the difference stated in the horizontal cleavage. Although the solid is displayed in the 3-D Euclidean physical space E³, no geometrical structure is presupposed except the local uniformity of color differences stated above. In Fig. 6C, all distances between horizontal or vertical neighbors, e.g., (L, j) and (L, j±2) or (L, j) and (L±2, j), are physically the same. Whether these chips appear to have the same difference d' and how d' is related to d are not in the logic of selecting standard chips. If the solid is sliced in an oblique direction so that L = j + constant, standard chips form a mesh consisting of regular triangles (slant cleavage). Fig. 6D shows a part of a slant cleavage passing through the central gray (0, 0, 0) in which L = j. All lines connecting points are supposed to represent color differences of the same size d.

 

 

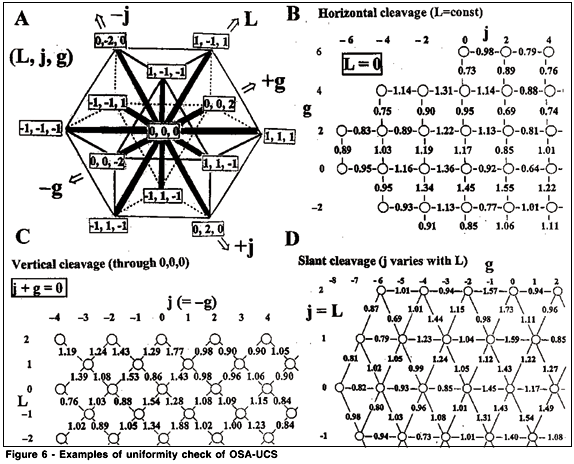
The uniformity of d between legitimate pairs of standard chips was tested by the use of 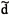, Equation (3) in Section 4^(23,27). Color differences at issue are in the range to which 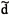is applicable and Munsell notation (H, V/C) of the OSA standard chips are known. Values given in Fig. 6B,C,D are 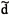_JK calculated for legitimate neighbors (J, K) in the respective cleavages. Means (M) and standard deviations (SD) of 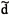_JK were obtained in each fixed direction, e.g., all horizontal neighbors at various levels of g or all vertical neighbors at various levels of j in Fig. 6B and along all oblique directions from right-left or along all oblique directions from left-right in Fig. 6C. The value of SD as an index for degree of non-uniformity is in the order of 0.21 - 0.27V. In the light that the instability in 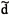is 0.34V, we can conclude that d_JK are of uniform size in the respective directions. However, M's of 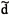_JK exhibit a systematic trend, though slight. When (J, K) differ in j or g only (L_J = L_K), e.g., horizontal and vertical directions in Fig. 6B and horizontal directions in D, 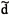_JK are in the order of 0.93 - 1.00V. When (J, K) include lightness difference (L_J ¹ L_K), e.g., oblique directions in Fig. 6C and D, _JK are in the order of 1.10-1.20V.

The OSA-UCS rhombohedral lattice solid covers almost the entire body of the Munell solid. As discussed in Section 3.3, the Munsell solid can be regarded as a 3-D manifold with local Euclidean metric. In so far as legitimate neighbors are concerned, chips in OSA-UCS satisfy the condition of local uniformity fairly well. Hence, it would be natural to expect that d' for non-legitimate oblique neighbor (j+2,g) and (j, g+2) in Fig. 6B is given by 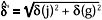, where d(j) and d(g) are two legitimate differences, between (j, g) and (j+2, g) and between (j, g) and (j, g+2). It was found, however, that 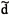' calculated for d' is systematically smaller than 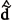' for 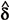' in all horizontal cleavages, (M of 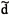') = 1.15V whereas (M of 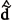') = 1.35V. This result casts doubt upon the natural expectation that the OSA-UCS rhombohedral lattice solid is locally Euclidean. Another interpretation is that this discrepancy is due to the possible non-additivity of the measure . This is an open question.

 

NCS (NATURAL COLOR SYSTEM) OF SWEDEN

This is another system of surface color based on human assessments. The principle according to which the standard color chips have been assembled is entirely different from that for the Munsell and that for the OSA-UCS. The NCS chips are selected so that they gradually vary in each of the three perceptual attributes. Chips are specified as (f, s, c) where s (blackness) varies from 0 to 100, c (chromaticness) from 0 to 90, each with the step of 10. In contrast to that Munsell V is only a function of the luminance reflectance Y and independent of H and C, s is not only a function of Y but also depends upon c and hue. Hue f is denoted such as Y50R, which means that this orange color is perceived as consisting of 50% of redness and 50% of yellowness^(28-29). In each sheet of f, standard chips are displayed as shown in Fig. 7A. This is a part of the sheet of Y50R. Chips of constant s are shown on an oblique line. The NCS color atlas includes a plate showing a hue circle. Most saturated colors of f are displayed on a circle. Hence, s and c of these colors are not constant. Fig. 7B shows a part hue circles for f having same s and c. The inner circle is for (s=20, c= 60) and the outer circle is for (s=10, c=70), each varying with the step of f = 20. Between R10B to B90G, chips of (s=10, c=70) are not available.

 

 

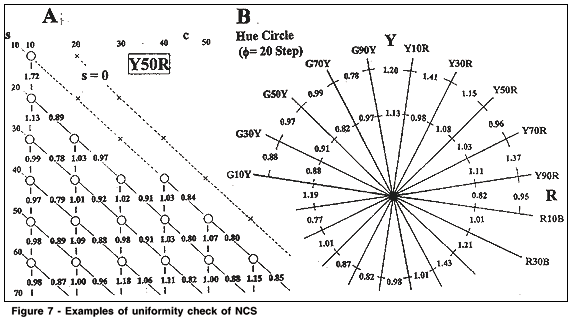
The purpose of NCS is to specify the appearance of an individual color in terms of its perceptual attributes, not to define difference between two colors. It is an interesting question to ask whether the gradual change of appearance in an attribute implies the uniformity of perceptual differences d between neighboring chips (J, K) along that attribute, e.g., (f, s, c) and (f, s±10, c) or (f, s, c) and (f, s, c±10), or (f, s, c) and (f±20, s, c). Numerical values in Figs. 7A, B are _JK calculated by Equation (3). In Fig. 7A (f=Y50R), mean (M) and standard deviation (SD) of _JK are 0.91V and 0.10V along the oblique c-axis and 1.11V and 0.16V along the vertical s-axis. The fact that SD is small in each axis and M is larger along s-axis is found in other sheets of f. In Fig. 7B, M and SD are 1.00V and 0.16V for the inner circle, 1.07V and 0.21V for the outer circle. That SD's are small in the respective attributes leads to an interesting conclusion that gradual changes in each attribute correspond to color differences d of a constant size between neighboring chips. In the logic of construction of NCS, it is not implied that d and hence M should be the same between the attributes. It is a matter of course in Fig.7 B that 20 interval of f means larger differences for more saturated colors of the outer circle than for less saturated color of the inner circle (M = 1.07V vs. 1.00V). In sheets of constant f, M along c-axis is 0.96V on the average with SD of 0.10V whereas M along s-axis is 1.15V on the average with SD of 0.05V.

 

CONCLUSION

For human, surface colors play an important role in recognizing objects in the visual space. A saurface color space is a systematization of this recognition process. In daily life, colors are denoted by names. Color naming is to divide a continuous color space into a few categories. As stated in 3.3, Munsell selected five principal hues taking the rainbow as an example in nature. This is about the same categorization as Newton first did with the spectrum he observed. Later, Newton added orange and indigo. It is known that as many as 200 different hues can be distinguished in the spectrum under ideal viewing condition⁽³⁰⁾. Dividing the spectrum into seven names is a categorization of aperture colors. As to surface colors, the number of discernible colors is a few million⁽³¹⁾ and color nomenclature is much richer, such as red, scarlet, crimson, maroon, etc. Clearly, how to divide a space of surface color into categories cannot be independent from culture and language. However, the systematizations of surface colors as discussed in this article are concerned with the cognitive process deeper than the level that is bounded to culture and language. Indow and Watanabe⁽³²⁾ demonstrated that human observers can memorize the scheme of Munsell notation and, without comparing with the Munsell standard chips, they can specify color samples in terms of (H, V/C).

 

REFERENCES

1. Metzger W. Optische Untersuchungen am Ganzfeld. II. Zur phänomenologie des homogenen Ganzfeld. Psychol Forschung 1930;13:6-29.         

2. Indow T. A critical review of Luneburg's model with regard to global structure of visual space. Psychol Rev 1991;98:430-53.         

3. Indow T. Global structure of visual space as a united entity. Math Social Sci 1999a;38:377-92.         

4. Indow T. Hyperbolic representation of global structure of visual space. J Math Psychol 1997;41:89-98.         

5. MacAdam DL. Visual sensitivities to color differences in daylight. J Opt Soc Am 1942;32:247-74.         

6. Brown WRJ, MacAdam DL. Visual sensitivities of combined chromaticity and luminance differences. J Opt Soc Am 1949;39:808-34.         

7. Nickerson D. History of the Munsell color system and its scientific application. J Opt Soc Am 1940;30:69-77.         

8. Newhall SM. The ratio method in the review of the Munsell colors. Am J Psychol 1939;52:394-405.         

9. Newhall SM. Preliminary report of the O.S.A. subcommittee on the spacing of the Munsell colors. J Opt Soc Am 1940;30:617-45.         

10. Newhall SM. A method of evaluating the spacing of visual scales. Am J Psychol 1950;63:385-418.         

11. Newhall SM, Nickerson D, Judd DB. Final report of the O.S.A. subcommittee on the spacing of the Munsell colors. J Opt Soc Am 1943;33:385-418.         

12. Indow T, Ida M. On scaling from incomplete paired comparison matrix . Jpn Psychol Res 1975;17:98-105.         

13. Indow T. Multidimensional studies of Munsell color solid. Psychol Rev 1988;95:456-70.         

14. Indow T. Global color metrics and color appearance systems. Color Res Applicat 1981;5:5-12.         

15. Indow T. Psychologically unique hues in aperture and surface colors. Die Farbe 1990;34:253-60.         

16. Indow T. Predictions based on Munsell notation. II. Principal hue components. Color Res Applicat 1999c;24:19-32.         

17. Indow T, Morrison ML. Construction of discrimination ellipsoids for surface colors by the method of constant stimuli. Color Res Applicat 1991;16:42-56.         

18. Indow T, Robertson AR, von Grunau M, Fielder GH. Discrimination ellipsoids of aperture and simulated surface colors by matching and paired comparison. Color Res Applicat 1992;17:6-23.         

19. Indow T. Indiscriminable regions, color differences, and principal hue vectors in Munsell space. Die Farbe 1993;39:15-23.         

20. Indow T. Predictions based on Munsell notation. I. Perceptual color differences. Color Res Applicat 1999b;24:10-8.         

21. Indow T. Parallel shift of judgment-characteristic curve according to the context in cutaneous color discrimination. In: Dowling CE, Roberts FS, Theuns P. editors, Recent Progress in Mathematical Psychology. Mahwah: Lawrence Erlbaum; 1998, p.47-63.         

22. Indow T. Principal hue curves and color differences. Color Res Applicat 1999d;24:297-9.         

23. Indow T. Color difference predicted by color component differences. Color Res Applicat 2002, in press.         

24. MacAdam DL. Uniform color scales. J Opt Soc Am 1974;64:1691-702.         

25. Nickerson D. History of the OSA Committee on uniform color scales. Opt News 1977;3:8-17.         

26. ASTM Committee E-12. ASTM standards on color and appearance measurement. Philadelphia: ASTM, 1991.         

27. Indow T. Uniformities in OSA-UCS and in NCS tested by color difference prediction based on principal hue components. In: AIC2001, The 9th Congress of International Color Association; 2001, p.95-196.         

28. Swedish Standard Institution. SS019102 Color Atlas. Stockholm: SIS; 1979.         

29. Hård A, Sivik L, Tonnquist G. NCS, Natural Color System – from concept to research and Application Part I and II. Color Res Applicat 1996;21:180-220.         

30. McLaren K. Newton's indigo. Color Res Applicat 1985;10:225-9.         

31. Pointer MR, Attridge GG. The number of discernible colours. Color Res Applicat 1998;23:52-4.         

32. Indow T, Watanabe M. Absolute identification of colors in Munsell notation: Trainability and systematic shifts. Color Res Applicat 1980;5:81-5.         

 

 

Correspondence to
Tarow Indow
Department of Cognitive Sciences, University of California Irvine, Irvine
CA 92612, USA
E-mail:[email protected]