ABSTRACT

Purpose: We have developed an instrument for computerized surgical videokeratography. A corneal central region of approximately 7.00 mm in diameter may be analyzed, providing the surgeon with information of the power and the astigmatism. Methods: The system is based on a fiber optic Placido disc projecting cone, which is attached to the objective lens of a Zeiss compatible surgical microscope. At the beam splitter we installed a monochromatic high resolution camera. A frame grabber is installed on a PC and images are digitized at a 480x640 resolution. Image processing is used for edge detection of rings. Results: Calibrating curves based on 4 spherical surfaces were generated and approximately 3600 points are calculated for each examination. Preliminary measurements on 10 healthy corneas were compared with those of an EyeSys System 2000 Corneal Topographer. Mean deviation was 0.05 for radius of curvature, 0.24 D for the power and 5.0 degrees for the cylinder. Conclusions: This surgical VKS, with some hardware and software improvements, may be used to reduce residual astigmatisms in conventional cataract and keratoplasty. It could also be used to gather preoperative data in corneal topography assisted LASIK.

Keywords: Corneal topography; Keratometry; Placido disc

RESUMO

Objetivo: Os autores desenvolveram um videoceratógrafo para uso durante a cirurgia. Uma região central da córnea de aproximadamente 7,00 mm de diâmetro pode ser analisada, fornecendo informação ao cirurgião sobre poder dióptrico e astigmatismo. Métodos: O sistema é baseado em discos de Plácido em forma cônica, iluminados por uma fonte de luz construída com fibras ópticas. O cone é acoplado à lente objetiva de um microscópio padrão Zeiss. Uma placa de captura é instalada num microcomputador IBM compatível e imagens de Plácido são digitalizadas numa resolução de 640x480 pontos. Processamento digital das imagens é utilizado para detecção dos discos de Plácido. Resultados: Curvas de calibração baseadas em 4 esferas foram geradas e aproximadamente 3600 valores de poder dióptrico são computados para cada exame. Exames preliminares em 10 córneas sadias foram comparados com exames nos mesmos olhos feitos num Videoceratógrafo Eyesys System 2000. O desvio médio padrão foi de 0,05 mm para o raio de curvatura, 0,24 dioptrias para o poder e 5 graus para o cilindro. Conclusões: Este videoceratoscópio cirúrgico poderá ser utilizado para reduzir o astigmatismo residual em procedimentos convencionais de catarata e ceratoplastia. Poderá também ser utilizado para colher dados imediatamente anteriores às em cirurgias refrativas (PRK e LASIK).

Descritores: Topografia da córnea; Ceratometria; Discos de Plácido

 

INTRODUCTION

Although most of the commercial videokeratographs (VKS) measure corneal curvature with reasonable accuracy ⁽¹⁾, none of them has been designed to be used during surgery. Other authors have addressed this issue ^(2-6), but none of them have developed a system which provides the benefits of a computerized system. To our knowledge none of them plot color maps of corneal shape as the surgery is taking place or use automated image processing based on the symmetry of the Placido disc images. Our claim is that there are certain surgical procedures which would benefit from such a system, such as cataract, corneal transplant (keratoplasty) and LASIK. In the case of cataract, for example, it may be used for reducing the incidence of residual astigmatisms. It has been verified with the Troutman Keratometer ^{(2-3, 6)}, that intrasurgical control of central corneal shape helps to diminish postoperative astigmatisms of up to 2.00D in conventional cataract surgeries. It became clear that an instrument that could measure corneal surface would be even more efficient ⁽⁶⁾. In a more recent study ⁽⁷⁾ it has been shown that LASIK procedures may be successfully assisted by preoperative corneal topography data. Although the authors did not use an intrasurgical device for these studies, we believe our system may be useful because preoperative data would be gathered with the patient in the position that the surgery would take place.

 

DEVELOPMENT

Basic apparatus

Like nonsurgical VKS, our system is also based on Placido's principle ⁽⁸⁾. We designed and constructed a high intensity conic concentric ring projecting pattern. This apparatus is attached to the objective lens of an Opto SM-2000 microscope (Rua André Ampére, 153 - 14 ^o andar - Brooklin Paulista\ CEP 04562-080 - São Paulo - SP - Brazil\ Tel. (011) 5506-8284 - Fax (011) 5506-5734) and light reflected off the cornea undergoes two distinct paths: its usual path through the microscope and a second path where the same beam of light is reflected by a beam splitter attached to the microscope's body. This second path leads the rays so they focus on the 480x640 CCD matrix of an attached monochromatic camera. The CCD grabs the same image seen at the ocular lenses by the surgeon ( Figure 1A).

The images are captured and saved in bitmap format on the computer's hard disc as the surgeon presses a foot switch. A 5V LED (light emitting diode) was adapted at the center of the Placido disc as a fixation point for the patient. During image digitalization the patient's eye must be aligned with the optic axis of the system. The microscope's light source must be turned off to avoid surrounding light reflections.

Image processing

Image processing starts right after digitalization. The algorithm finds the LED position and from this point starts the edge detection of the Placido discs. Other authors ⁽⁵⁾ describe methods that scan the image in horizantal lines and determine edges by difference in the intensity of gray levels. We suggest that transforming the Cartesian plane (x,y) of the Placido image in a polar coordinate system (theta, phi) with origin at the LED makes the problem of edge detection straightforward because of the near polar symmetry of the discs. By "scanning" the image in the radial direction ( Figure 2A) this problem can be reduced to a one dimensional image processing task.

By plotting the intensity of gray level (0-255) for polar angles from 0 to 360 degrees we obtain curves with high and low levels of gray. The portions of higher levels are associated with bright discs on the image, and regions of lower levels are associated with dark discs.

By smoothening these curves to reduce noise and then applying the first derivative to each point, we obtain a second curve where each peak represents the edge between dark and bright discs. We then take the absolute value of each point on this second curve and then apply a line of threshold which determines the edge points. Because we used an algorithm based on calibration curves, the level of thresholding used to determine the edge location can be arbitrarily determined, as long as it is value that allows most of the edge points to be detected.

Calculating radius of curvature and power

Several authors have explored the nontrivial problem of calculating corneal shape based on Placido images. Some insights may be found in ^(9-17), just to name a few. We will describe here only the method that we used, which may be described as the calibrated sphere algorithm ⁽¹⁸⁾ or the look-up table method. Either way, the method is based on images collected from a set of calibrating spherical surfaces and the output furnishes axial curvature. A good description of ways in which to calculate other curvatures and the advantages of each one, based on axial curvature, is given in ^(14,15).

For the calibration data set we used 4 spherical glass surfaces of different radii (7.73, 8.06, 8.34 and 8.91 mm) and measured edges for all of them using the algorithm described above. From this information we used linear regression to construct the graph of radius of curvature versus edge distance shown in Figure 2B. Each line corresponds to the interpolation of data from the 4 surfaces, for each edge. Line 1, for example, represents approximation of 4 data points for edge number 1. The other lines in the graph are generated analogously. In this way we found the parameters a and b for the equation of each line (1) and saved these values as ASCII files. r stands for radius of curvature and b stands for distance (in pixels). From each equation one may then calculate radius of curvature for any given edge point of an arbitrary surface. To improve performance of the algorithm we implemented a look-up table of values for each border, containing border distance on one column and radius of curvature on the other. In this ways values may rapidly be accessed.

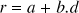
The diopter at each point is calculated using the formula where n _c is the index of refraction of the cornea and n _air is the index of refraction of the air. For n _c we used the Gullstrand reduced schematic eye index of refraction 1.3375, normally used for keratometers. And for n _air the value 1.000 was used. The denominator is the local radius of curvature in meters.

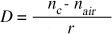
By using this method several thousand points may be calculated (at most 360x10=3600). We used visualization techniques used by most commercial topographers, that is, flat color maps, originally suggested by ⁽¹²⁾. The curvature data points are interpolated in the radial direction (Figure 5) using cubic splines ⁽¹⁹⁾ for each semi-meridian to generate a smooth two dimensional color map. A color table with 15 different colors is associated with variable values of radius of curvature and diopter. The minimal and maximum values of the table vary in accordance to the mean diopter value of data for each examination.

 

RESULTS

The instrument was originally tested on several spherical surfaces (12 total) different from those used for calibration (radius varying from 6.78 to 8.80 mm). As expected, almost single colored maps were displayed, with approximately constant values of curvature. Mean deviation for radius was 0.02 mm and 0.12 for diopter.

After tests on artificial surfaces, preliminary measurements were made in 10 healthy corneas of 5 adult volunteers (2 females and 3 males, ages between 22 and 45). The procedure was fully explained and formal consent was obtained in all cases. For comparison the same corneas were measured in an EyeSys Corneal Topographer with color map (axial) display. We generated a computer algorithm to read and compare data from the EyeSys topographer with data from our system. By using a small ruler (markings of 10 ^-2 cm) we determined the scale factor of our instrument (pixels/mm) and also that of the EyeSys topographer. We could then precisely determine which region in the topography maps corresponded to our measurements and therefore compare values for each data point. In figures 3 and 4 we show two cases for visual comparison of results.

Quantitative results were as follows: mean deviation in radius of curvature for all examinations was less than or equal to 0.05 mm for 8 cases. Corneal astigmatism deviations were less than or equal to 0.18 D for 7 of all cases. For cylindrical axis deviation was less than or equal to for 5 degrees for 6 of all cases. Mean time for each examination was 14.3 s, including image processing and generation of color map. Graphs of curvature versus polar angle for a specific radial distance were also implemented. These provide a simple and fast way for the surgeon to analyze the astigmatism of the surface at a specific region.

 

DISCUSSION

In this article we describe the development of a novel instrument, which may be described as a surgical VKS. Preliminary tests on healthy corneas indicate that the instrument may be applied in diminishing post-astigmatisms common to surgeries such as cataract and corneal transplant. We should point out that there are new techniques for cataract surgery that need only small incisions and therefore cause little distortion after sutures, but in many countries the traditional technique is still in use. We should also notice that there are cases of corneal transplant where the cornea becomes so distorted that the Placido discs are virtually impossible to analyze.

Other possible applications should be in surgeries that use intrastromal rings to correct refractive errors ⁽²⁰⁾, making it possible to determine more precisely how many diopters were corrected; and in topography assisted LASIK surgeries ⁽⁷⁾.

The image processing phase is fast and efficient because it is based on the polar symmetry and good contrast of the Placido discs. It requires only one mouse click and takes only about 4 s. Other systems require several user clicks ⁽⁵⁾. The system is also very easy to maintain and install and may also work on a regular Notebook PC, provided that the compatible hardware is used. This adds a great deal of convenience in terms of carrying the system to different surgery rooms. Surgeon's opinions during the examination process was that the system is quite easy to mount and use, but modifications should be introduced so the process would not require mouse clicks and attention with software manipulation during surgery.

Some improvements to the system should include: a smaller Placido disc system to improve the surgeon's freedom when accessing the patients eye with surgical tools; a method that provides correct alignment of the patient's head, to avoid wrong axis measurements and even to account for cyclotorsion of the eye globe; attachments of more rings at the center of the Placido disc in such a way that the 1.5 mm central region can be mapped with more accuracy.

 

ACKNOWLEDGMENTS

We would like to thank the Escola Paulista de Medicina - UNIFESP for providing the room in which we installed and tested the system, and also for allowing us to use their Eyesys System. We would like to thank Professor Stanley Klein, Ph.D., Thom Carney, Ph.D., Corina van de Pol, Ph.D., and John Corzine, O.D., from the School of Optometry, University of California at Berkeley, for their tremendous help and interesting ideas. We would also like to thank the following institutions for financial support: FAPESP (Fundação de Amparo à Pesquisa do Estado de São Paulo - Brazil, CNPq - Conselho Nacional de Desenvolvimento Científico e Tecnológico - Brazil).

 

 

REFERENCES

1. Sanders, Donald R, Koch, Douglas D. An atlas of corneal topography. 2nd ed. New Jersey: Slack; 1993.         

2. Troutman RC, Buzard KA. Corneal astigmatism. 3rd ed. St. Louis: Mosby Year Book; 1989.         

3. Troutman RC, Kelly S, Kaye D, Clahance AC. The use and preliminary results of the Troutman Surgical Keratometer in cataract and corneal surgery. Trans Am Acad Ophthalmol Otorarygol 1977;83:232-8.         

4. Amoils SP. Intraoperative Keratometry with the oval comparator (Astigmometer). Br J Ophthalmol 1986;70:708-11.         

5. Igarashi H, Kojima M, Igarashi S, Yoshida A, Cheng HM. A simple and effective video keratometric system. Acta Ophthalmol. Scand 1995;73:336-9.         

6. Troutman RC. Surgical keratometer in the management of astigmatism in keratoplasty. Ann Ophthalmol 1987;19:473-4.         

7. Wiesinger-Jendritza B, Knorz MC, Hugger P, Lierman A. Laser in situ keratomileusis assisted by corneal topography. J Cataract Refract Surg 1998; 24:166-74.         

8. Placido A. Novo instrumento de exploração da cornea, Periodico d'Oftalmológica Practica, Lisboa 1880;5:27-30.         

9. Mandell RB, St Helen R. Mathematical model of the corneal contour. Br J Physiol Optics 1971;26:183-97.         

10. Mandell RB. The enigma of the corneal contour. CLAO J 1992;18:267-73.         

11. Mammone RJ, Gersten M, Gormley DJ, Koplin RS, Lubkin VL. 3D Corneal modeling system. IEEE Trans Biomedical Eng 1990;37:66-73.         

12. Klyce SD. Computer-assisted corneal topography, high resolution graphics presentation and analyses of keratoscopy. Invest Ophthalmol Vis Sci 1984;25:426-35.         

13. Klein SA. A corneal topography algorithm that produces continuous curvature. Optom Vis Sci 1992;69:829-34.         

14. Klein SA, Mandell RB, Shape and refractive powers in corneal topography. Invest Ophthalmol Vis Sci 1995;36:2096-109.         

15. Klein SA, Mandell RB. Axial and instantaneous power conversion in corneal topography. Invest Ophthalmol Vis Sci 1995;36:2155-9.         

16. van Saarlos, Paul P, Constable IJ. Improved method for calculation of corneal topography for any photokeratoscope geometry. Am Acad Optometry 1991; 68:960-5.         

17. Halstead MA, Barsky BA, Klein SA, Mandell RB. A spline surface algorithm for reconstruction of corneal topography from a videokeratographic reflection pattern. Optom Vis Sci 1995;72:821-7.         

18. Halstead Mark A. Efficient techniques for surface design using constrained optimization. . Berkeley: University of California; 1996.         

19. Barsky BA. Computer graphics and geometric modeling using Beta-splines. New York: Springer-Verlag; 1988.         

20. Burris TE, Holmes-Higgin DK, Silvestrini TA, Scholl JA, Proudfoot BS, Baker PC. Corneal asphericity in eyebank eyes implanted with the intrastromal corneal ring. J Refract Surg 1997;13:556-67.         

 

 

* Mantém vínculo com a EyeTec Equipamentos Oftálmicos Ltda.( www.eyetec.com.br), empresa que fabrica a versão comercial do instrumento apresentado.

¹ Pesquisador junto ao IFSC (Instituto de Física de São Carlos)-USP, Diretor de Pesquisa da Eyetec Equipamentos Oftálmicos Ltda.
² Diretores do Departamento de Projetos Mecânico e Eletrônico da Eyetec Equipamentos Oftálmicos.
³ Pesquisadora junto ao IFSC (Instituto de Física de São Carlos)-Universidade de São Paulo e Projetista da Opto Eletrônica S/A.
⁴ Professor do Instituto de Físisca de São Carlos-Universidade de São Paulo.
⁵ Doutor no Setor de Cirurgia Refrativa do Departamento de Oftalmologia da Universidade Federal de São Paulo.

Endereço para correspondência: Av. Dr. Carlos Botelho, 1465 - São Carlos (SP) CEP 13560-250. E-mail: [email protected]

Nota editorial: Pela análise deste trabalho e por sua anuência sobre a divulgação desta nota, agradecemos ao Dr. Milton Ruiz Alves.
Recebido para publicação em 26.03.2001
Aceito para publicação em 20.08.2001