ADVANTAGES AND DISADVANTAGES OF THE prism-diopter UNITY
Angular measurements are defined by their respective arc lengths. Therefore, they retain their absolute and direct proportionalities between different quantity expressions: 50º is exactly half of 100º or ten times 5º, as well as 50 × (180/π) radians.
However, such unequivocal relationships among angles may not be easily reproduced in many instances. In such cases linear lengths become more practical. Notably, the angular distance between two straight lines, or directions, may also be given as a ratio of their respective linear lengths. One such ratio defines the traditional angular unity for measurements in strabismus as the prism-diopter. It was proposed by Prentice in 1890, as the angle formed by a deviation of 1 cm taken at 1 m from the point of observation(1) (Figure 1). The unity prism-diopter is symbolized by the capital Greek letter delta, written as a superscript to the measured quantity (Δ). For example, fifteen prism-diopters is written as 15Δ.
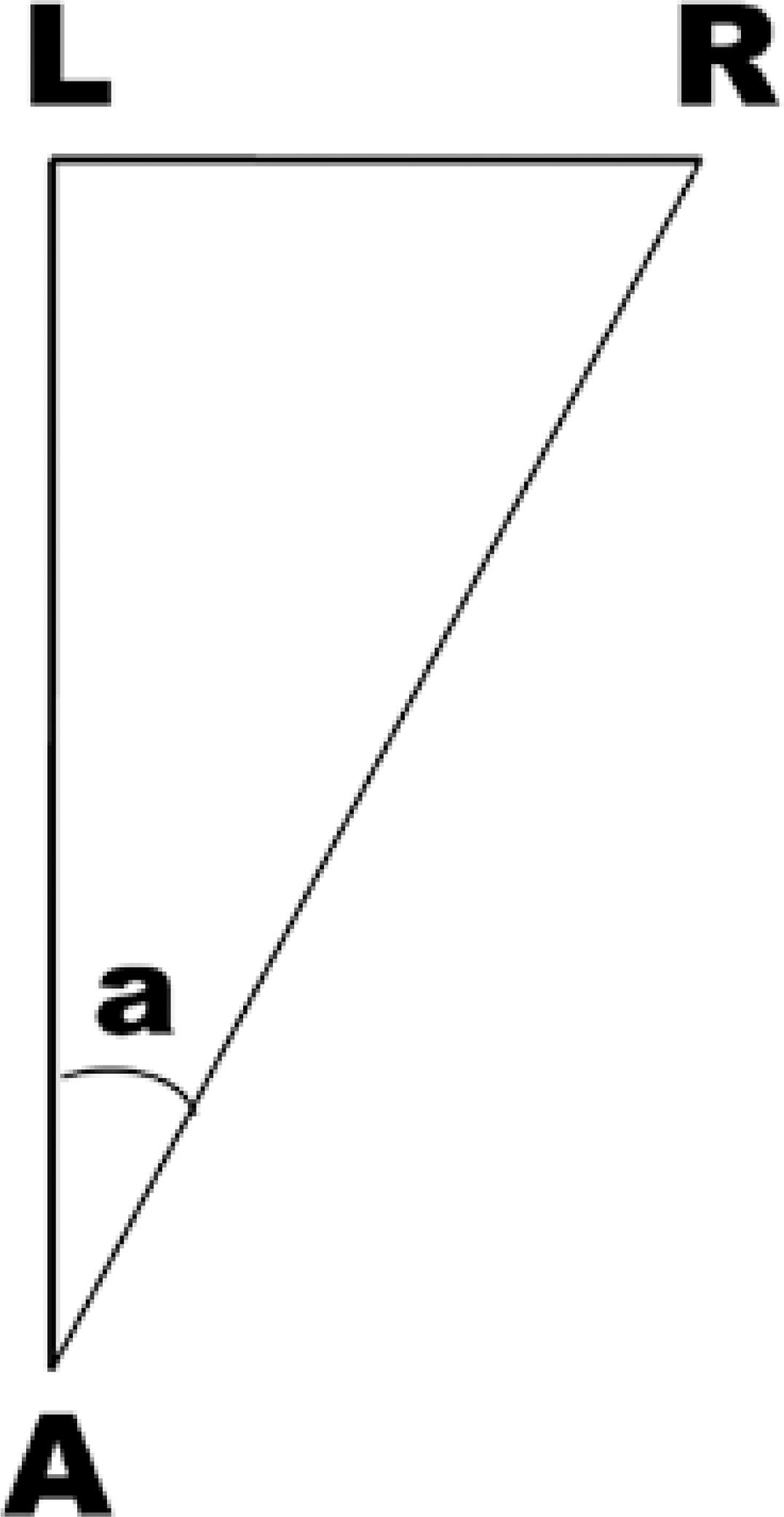
Figure 1 The basic geometric relationships used to define the prism-diopter. The ratio between the side LR, when expressed in centimeters, and the side AL, when expressed in meters, gives the value of the angle LÂR in prism-diopters. The actual angle shown (since LA = 2 LR) is P=50Δ (while a ≈ 26.565°).
This is a very practical proposition because it allows an angle to be expressed as a relationship between linear distances. For instance, if a subject fixates an object placed at a distance of 4 m and observes duplicate images separated by 80 cm, the angle of deviation can be easily calculated as 80 cm/4 m=20Δ. The "Maddox cross", classically used for measurements of ocular deviations, is simply a metrical scale in a wall, where each regular interval of one prism-diopter represents the centesimal part of the distance between such a wall and the observed subject. For instance, if the distance from the subject (from whom the ocular deviation will be measured) to the scale in the wall is 5 m, each interval equivalent to one prism-diopter must be 5 cm.
It should be noted that the definition of prism-diopter (P') implies two different metrical unities: centimeter (cm) for the "deviation" (LR in Figure 1) and meter (m) for the "distance" (AL in Figure 1) at which the measurement is realized. Thus, one of the quantities is expressed by a metrical unity that is the centesimal part of the other. To equalize the measurements and allow the definition to be valid for any scale of unities (e.g., inches), P' has to be expressed as P:
P' = LR (cm)/AL (m) → P = 100 LR/AL
The conversion of such a ratio to the corresponding arcuate measurement, that is, the relationship between the linear lengths ratio and the angle expressed in arc degrees (or in radians), is calculated trigonometrically. Thus, the angle (a) in arc degrees is related to its value expressed in prism-diopters (P) by
a = arc tan (P/100) or P = 100 tan a
so that, if LR = 1 (cm) and AL = 1 (m), then P=1Δ, and therefore a = arc tan 0.01 ≈ 0.572938697º. Or, conversely, if a=1º, then tan 1º ≈ 0.017455064 ≈ P/100, and therefore P ≈ 1.745506493Δ. Note also that it is generally accepted that 4º ≈ 7Δ. Furthermore, note that the prism-diopter is numerically almost equal to the centesimal part of the radian, the centrad (= 1.8/π = 0.572957795º), a unity proposed by Dennet(2) at the same time that the prism-diopter was proposed (1888-1890). In fact, for the great majority of practical purposes they can be considered to be equivalent, since one prism-diopter is only 0.003333133% smaller than one centrad, and 30001Δ ≈ 30000 centrads.
However, while arithmetical operations are valid for quantities expressed in centrads (or arc degrees, or their submultiple unities), such simple calculations are not correct for values expressed in prism-diopters. Thus, the angle of 30Δ is not three times the angle of 10Δ, half of 60Δ, or the result of 18Δ + 12Δ or 50Δ - 20Δ. The respective conversions must follow a relatively lengthy procedure whereby the values in prism-diopters have to be initially transformed into arc degree values (or centrads). The arithmetical operation can then be completed before the resultant figure is converted back to prism-diopter unities. The respective errors (e) between the correct values and those produced by the simple arithmetical operations, for the above examples, is shown below:
10Δ (=5.711º) × 3 = 17.132º = 30.825Δ (e=2.75%)
60Δ (=30.964º)/2 = 15.482º = 27.698Δ (e=-7.67%)
18Δ (=10.204º) + 12Δ (=6.843º) = 17.047º = 30.662Δ (e=2.21%)
50Δ (=26.565º) - 20Δ (=11.310º) = 15.255º = 27.273Δ (e=-9.09%)
Note that although every incorrectly supposed result (of the arithmetical operation) can be the same (30Δ), the correct answer and the respective error (e) are always different. Additive (or multiplicative) operations produce values greater than 30Δ, while subtractions (or divisions) produce values smaller than 30Δ. For larger values, the discrepancies obtained when performing arithmetical operations become highly significant:
20Δ (=11.310º) × 4 = 45.240º = 100.840Δ (e=26.05%)
160Δ (=57.995º)/2 = 28.997º = 55.425Δ (e=-30.72%)
50Δ (=26.565º) + 30Δ (=16.699º) = 43.264º = 94.118Δ (e=17.65%)
170Δ (=59.534º) - 90Δ (=41.987º) = 17.547º = 31.621Δ (e=-60.47%)
Note that while the interval between 1Δ (=0.572939º) and 2Δ (=1.145763º) is 0.572824º (=0.999800Δ), that between 41Δ (=22.293629º) and 42Δ (22.782406º) is 0.488777º (=0.853097Δ), and that between 121Δ (=50.428097º) and 122Δ (=50.659482º) is 0.231385º (= 0.403845Δ). Thus, equal prism-diopter intervals progressively lessen as the figures become higher. Furthermore, 90º corresponds to infinite prism-diopters, while prism-diopter values corresponding to angles greater than 90º and smaller than 180º are negative, and numerically decrease with the increment of the angle. This is obviously a very inconvenient circumstance, since increasing values of a positive (eso) deviation may be interpreted as decreasing values of a negative (exo) deviation (Table 1). Conversely, greater values of a negative (exo) deviation may be interpreted as smaller values of a positive (eso) deviation.
Table 1 Values of angles in arc degrees (a), centrads (c=π.a/1.8), prism-diopters (P=100 tan a), and the new unity of deviation, U=200 (csc a - ctn a)
| a | c | P | U | (P - c)/c | (U - c)/c |
|---|---|---|---|---|---|
| 1º | 1.745 | 1.746 | 1.745 | 0.010% | 0.003% |
| 5º | 8.727 | 8.749 | 8.732 | 0.255% | 0.064% |
| 10º | 17.453 | 17.633 | 17.498 | 1.028% | 0.255% |
| 20º | 34.907 | 36.397 | 35.265 | 4.270% | 1.028% |
| 50º | 87.266 | 119.175 | 93.262 | 36.565% | 6.870% |
| 90º | 157.080 | ∞ | 200.000 | ∞ | 27.324% |
| 135º | 235.619 | -100.000 | 482.843 | -142.441% | 104.925% |
| 180º | 314.159 | 0 | ∞ | -100.000% | ∞ |
| 270º | 471.239 | ∞ | -200.000 | ∞ | -142.441% |
BASICS OF A NEW UNITY OF ANGULAR MEASUREMENTS
I propose a very simple modification to the definition of the prism-diopter unity, originally proposed by Prentice, that does not substantially alter his idea. This modification avoids some of the inconveniences of the original unity and reduces the quantitative distortions produced by its measurements(3,4). The new unity, which retains the concept of an angle implying a separation of 1 cm at 1 m, is hereafter designated the unity of deviation, or the prismatic unity, and is represented by the capital Greek letter lambda (Λ) as a superscript to the quantity of the measurement. This allows for differentiation from the prism-diopter, represented by the capital letter delta, Δ. However, it employs symmetrical distribution relative to the vertex point (of observation), instead of the asymmetrical distribution used in Prentice's proposition (Figure 2).
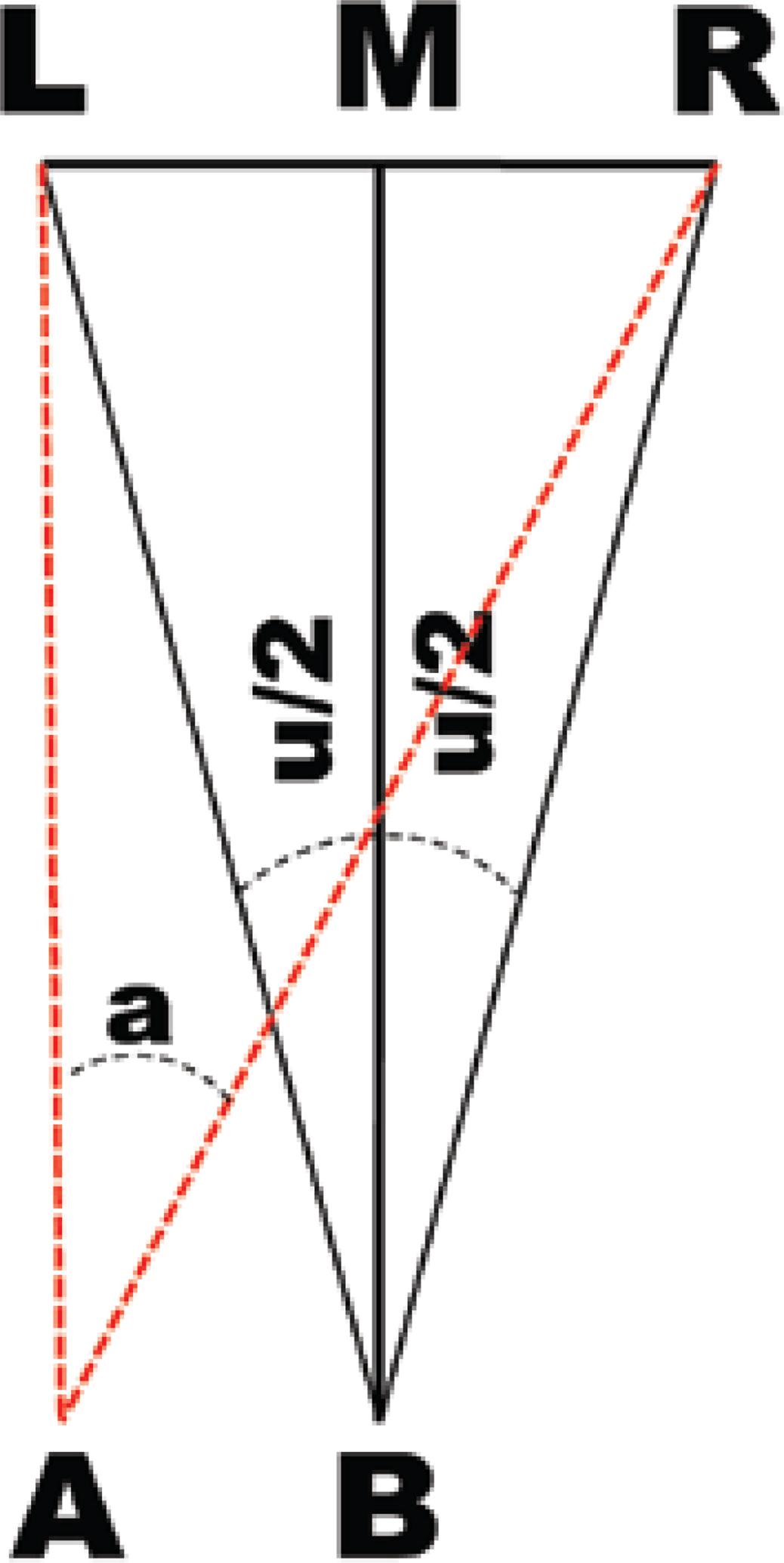
Figure 2 The new unit for measuring angular deviations (1Λ) is defined by the angle u=LBR, formed by the distance of 1 cm (= LR) between two equidistant points (L and R) of the point of observation (B), taken perpendicularly at a distance of 1 m (=BM). One half of this angle (u/2 = LBM = MBR) is expressed as 100 LM/MB = 100 RM/MB = tan (u/2). Here, the angle LBR is expressed by the new unity U as 50Λ, and a (angle LAR) is expressed in prism-diopters as P=50Δ. But note that while u ≈ 28.072° (hence U=50^, but P=53,333Δ), a ≈ 26.565° (hence P=50Δ, but U=47.214^).
The respective mathematical relationships become:
(u/2) = arc tan (U/200) or U = 200 tan (u/2)
so that, if 2 LM = 2 MR = LR = 1 (cm) and BM = 1 (m), then U = LBR = u = 1Λ. Hence, (u/2) = arc tan (1/200) = 0.28647651º, so that u=0.57295302º. Note that the differences between the values a and u are expressed in degrees of an arc, and are found only from the fifth decimal figure (u is 0.0025% greater than a). Therefore, the difference of 1Λ to the centrad is still smaller (0.000833319%, or 120,001Λ ≈ 120,000 centrads).
Conversely, if u=1º, then tan (u/2) = 0.008726867, hence U=1.745373558Λ. Note that the approximation 4º = 7Λ remains valid. Obviously, with the new proposition (which retains the concept of an angular measurement by means of linear lengths), the lack of proportionality of the so expressed magnitudes related to those respectively expressed in degrees of arc remains. Thus, as for Prentice's prism-diopter unity method, the use of arithmetical operations with quantities expressed by the new unity of angular deviation are invalid. However, the observed distortions are significantly smaller, particularly when large angular values are considered. For the previously calculated magnitudes:
10Λ (=5.725º) × 3 = 17.174º = 30.202Λ (e=0.67%)
60Λ (=33.398º)/2 = 16.699º = 29.354Λ (e=-2.15%)
18Λ(=10.286º) + 12Λ (= 6.867º) = 17.153º = 30.163Λ (e=0.54%)
50Λ (=28.072º) - 20Λ (= 11.421º) = 16.651º = 29.268Λ (e=-2.44%)
For higher values the errors in some instances remain large. However, they are much more acceptable than those obtained with the prism-diopter unities:
20Λ (=11.421º) × 4 = 45.685º = 84.246Λ (e=5.31%)
160Λ (=77.320º)/2 = 38.660º = 70.156Λ (e=-12.30%)
50Λ (=28.072º) + 30Λ (= 17.062º) = 45.134º = 83.117Λ (e=3.90%)
170Λ (=80.729º) - 9vv (= 48.455º) = 32.274º = 57.866Λ (e=-27.67%)
The trigonometric formulas which relate the angles a and u, when a = 2 u are:
tan a = [(2 tan u/2)]/[1 - tan2 (u/2)]
or
tan (u/2) = (1 - cos a)/sen a = csc a - ctn a
from where the conversion of the values of U (in this new unity of deviation) to P (in prism-diopter unities) result in P = 40000 U/(40000 - U2)
while the conversion from P to U results in
U = (200/P) [-100 + (1002 + P2)1/2]
For instance, if P=100Δ (=45º), U=82.843Λ. If U=100Λ (=53.130º), P=133.333Δ. But if U=200Λ (=90º), P=∞. And if U=300^ (=112.62º), P=-240Δ. Table 1 shows the relationships between values expressed in arc degrees, centrads, P and U, as well as the relative errors when such unities (P and U) are used.
An error of 5% for values referred to in prism-diopters relative to the corresponding values in centrads (c) is reached for an angle of a=21.5529636º (c=37.617 crad, P=39.498Δ, U=38.067Λ). This angle is frequently observed in clinical practice. However, the same error of 5% for values produced by the new unity of deviation relative to the values expressed in centrads is only reached for an angle of 2 u = a = 43.1059274º (c=75.234 crad, P=93.598Δ, U=78.996Λ). This angle is exactly double that which gives the same error when the prism-diopter unities are used. (For such an angle, the error in prism-diopters is 24.41%).
With respect to the refractive action of a prism, it is important to note that the prism-diopter unity is based on the concept of a deviation occurring at only one surface of a prism [called the Prentice's condition (Figure 3a)]. However, the new unity of angular deviation is related to the concept of a symmetrical deviation, known as the condition of the minimum deviation (Figure 3b). Coincidentally, this is the deviation with which the prism is conceptually quantified.
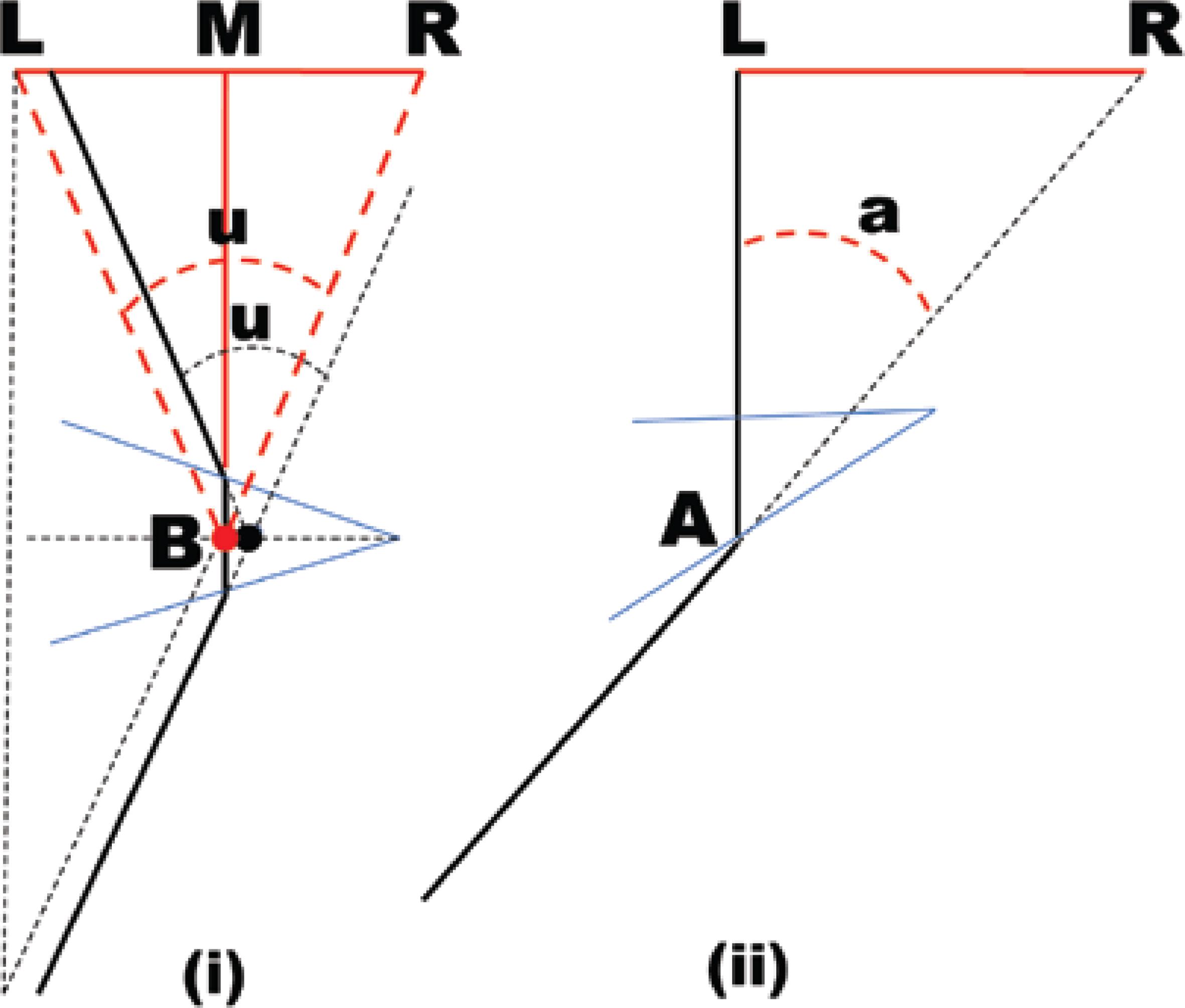
Figure 3 (i): The criteria with which the new unity for measuring angles is defined is that of the condition of the minimum deviation. This is classically accepted as the most convenient for expressing the “power” of deviation (i.e., the value) of a prism. In this condition, the incident and the emergent rays are completely symmetrical and the path of the light within the prism is perpendicular to its bisector. (ii): The unitary angle of a prism-diopter is related to the concept of a deviation occurring at only one of the refractive surfaces of a prism, the so-called Prentice’s condition (angle of incidence is zero, i.e., the wavefronts of the incident light perpendicular to the “entrance” face; or angle of refraction zero, i.e., wavefronts of the refracted light perpendicular to the “exit” surface). Note that although the distances LA=MB, besides LR, are equal for both conditions, the angle LAR=a (whose tangent expresses one-hundredth of prism-diopters, tan a=0.01 P), is not equal to the angle LBR=u (where the tangent of each half-part expresses five-thousandths of the new unity, tan (u/2) = 0.005 U).
The concept of measuring angles by linear dimensions may also be used for other unities of length. For instance, if a diplopia subject observes that duplicate images of an object placed at 5 ft appear to be separated by 30 in, the deviation may be calculated as equal to (100/12) × (30/5) = 50^. Here, the expression (100/12) represents 100 times the quantity of inches in a foot (12), that is (25/3) ft/in. Therefore, 3 in/ft = 25^, which also means that for a distance of 15 ft, each 9 in equals 5^ (100/12) × (9/15) = 5^ = (25/3) (ft/in) × (9/15) (in/ft).
Similarly, one may also use another ratio for expressing the measurement of an angle if the length measurements are given in inches and yards (1 yd = 36 in). Thus, the angle is given by (100/36) (yd/in) × the length measurements (in/yd). Hence, by approximation, 9 in/yd = 25^ and angle (^) ≈ 2.8 × (in/yd). Thus, a diplopic separation of 50 in for a distance of 7 yd represents a deviation of approximately 20^.
PRACTIVAL CONSIDERATIONS AND CONCLUSIONS
1) The very practical conveniences of using the dimensional relationships between straight lines for measuring angles instead of considering the arcs of circles, originally led to the introduction of the prism-diopter as a unity of angular measurements. Due to its advantages, the prism-diopter became commonly used for measuring angles in ophthalmological practice. However, its non-linear scale represents a major practical drawback. It is advisable to retain the advantages of using relationships between straight dimensions (linear distances) for measuring angles. It is also scientifically advantageous to decrease the implicit errors of the scales using such a concept. The new unity for angular measurements presented here fulfills both of these requirements.
2) The adoption in ophthalmological practice of the new unity proposed for measurements of angles of binocular deviations, does not require that prisms where respective values of a face are given in prism-diopters, need to be abandoned. It is sufficient to correct the angular values by the proper rate of conversion (using a formula or a table).
3) The new unity of angular measurements is defined according to a geometrically symmetrical condition. This is similar to the conditional criteria conventionally adopted to express the value of a prism (that is, the conceptual condition of the minimum deviation, Figure 3a), and is in contrast to the criteria by which the prism-diopter is defined [a deviation occurring at only one surface of a prism, the Prentice's condition (Figure 3b)].
4) The value of the new unity for measuring angular deviations (1Λ) is almost identical to the value of the prism-diopter (1Δ) and the centrad (1 crad), but is positioned between the two:
1Λ = 34' 22.631" = 0.57295302º = 1.000025001Δ = 0.999991666 crad
5) The small differences between them (1Λ is 0.0025% greater than 1Δ and 0.0008% smaller than 1 crad, while 1Δ is 0.0033% smaller than 1 crad) can be considered negligible for most practical purposes. In a scale constructed for use at a distance of 5 m, the difference in size of intervals expressed by the new unity and the prism-diopter is only 1.25 μm. Because the difference between the new unity of angular measurements and the value of the centrad is less than the difference between it and the value of the prism-diopter, the new unity should be preferentially used.
6) Although the differences between the absolute values of the arc (angle) of one prism-diopter (1Δ), one (new) unity of angular measurements (1Λ), and one centrad may be considered negligible, the scales with which they are constructed present very important discrepancies. While the scales for crescent angles are always linearly crescent for centrads, they are periodically changed for the unities based on linear measurements (the prism-diopter and, or, the proposed new unity). The critical point of periodicity at which the measurements based on linear unities reach infinite values is 90º for the prism-diopters scale, and 180º for the new unity of angular measurements. From such points, although the actual angles follow a progressive crescent, the corresponding measurements show inverted signals and progressively decrease to zero (Table 1). Therefore, the use of prism-diopter unities to quantify binocular strabismic deviations between 90º and 180º (which although relatively rare are sometimes encountered), is invalid.
7) When prism-diopter unities are used, angular errors with the ordinarily accepted level of statistical significance (5%) occur for measurements above the value of 39.5Δ (equivalent to about 21.6º). This represents a relatively frequently observed clinical strabismic deviation and is within the range of many possible ocular rotations. If the new unity is used the same error will only occur with a measurement of 93.6 prism-diopters. This is equivalent to about 43.1º, or twice the angle with which the limit for the prism-diopter range may be applied.
8) Errors of calculation caused by an improper application of simple arithmetical operations applied to angular measurements expressed by non-linear scales, are far greater when prism-diopter unities are used.
9) Clinical procedures for the examination of binocular deviations directly ahead of the subject are based on a symmetrical condition (the referential point for the binocular fixation is symmetrically placed in front of the subject, between the eyes), as defined by the new unity. Measurements based on the prism-diopter concept require rigorous asymmetrical conditions. That is, they require translational displacements of the head, or of the referential point of fixation, for the correct adjustment of direction of the visual axis of each "fixating" eye (Figure 4).9) Clinical procedures for the examination of binocular deviations directly ahead of the subject are based on a symmetrical condition (the referential point for the binocular fixation is symmetrically placed in front of the subject, between the eyes), as defined by the new unity. Measurements based on the prism-diopter concept require rigorous asymmetrical conditions. That is, they require translational displacements of the head, or of the referential point of fixation, for the correct adjustment of direction of the visual axis of each "fixating" eye (Figure 4).>
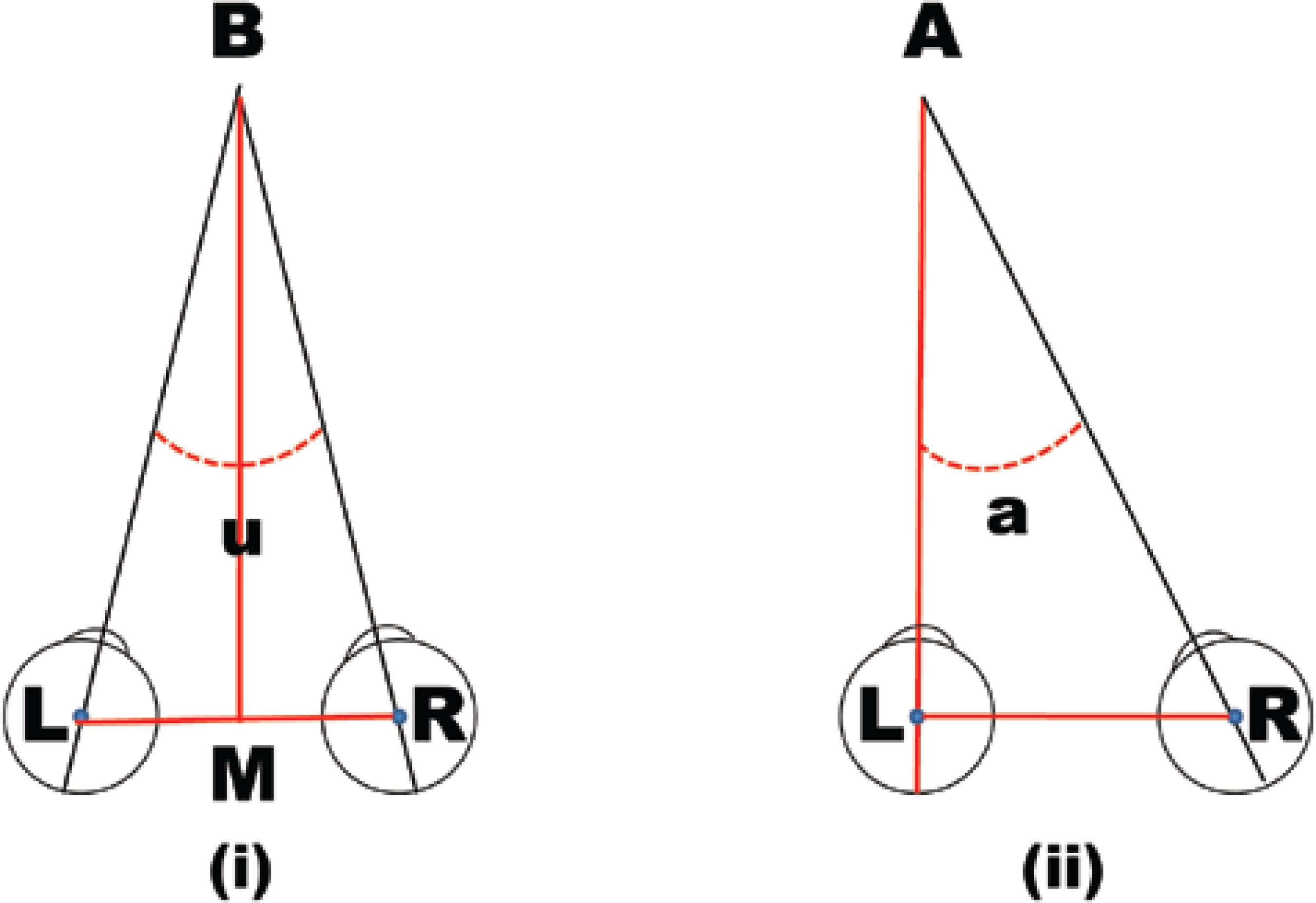
Figure 4 (i): Usual examination position for binocular convergence or for the measurement of a strabismic deviation, with the object of fixation (B) symmetrically placed before the eyes (L and R). The measurement may be alternatively taken with the fixation of each eye, without changing the position of the object of fixation or of the eyes (head). (ii): Asymmetric convergence measured before one eye (L), or measurement of a strabismic deviation of the right eye (R), with the left eye (L) directing the fixation. For a fixation measurement of the right eye (R), the position of the object (A), or of the head, has to be changed.
AN EXTENSION OF THE CONCEPT
It may be noted that the superior performance of angular measurements and operations obtained with the use of the new unity, as compared to the prism-diopter unity method, results in the bipartition of the conceptual angle of definition with a corresponding trigonometrical compensation. In other words, since the quantity in prism-diopters is one hundred times the tangent of the angle (P = 100 tan a), the quantity with the new unity (U) is two hundred times (i.e., twice) the tangent of half the angle (but not half the value of the tangent of the same angle), U = 200 tan (a/2). Hence 2 P tan (a/2) = U tan a → [2 tan (a/2)]/tan a = U/P = 1 - tan2 (a/2)
If, however, instead of partitioning the angle into two halves it were divided into thirds or quarters, the respective conversions for the new unities (U' and U") would become:
a/3 = arc tan (U'/300) or U' = 300 tan (a/3)
and a/4 = arc tan (U"/400) or U" = 400 tan (a/4)
Or, by generalization
a/n = arc tan (Z/100 n) or Z=100 n tan (a/n)
where n may assume any numerical value.
When related to the traditional values of P, the relationship becomes:
n P tan (a/n) = Z tan a
The greater the value of n (i.e., the greater the partition of the fundamental angle for the definition of the consequent unity), the closer the value of the defined unity becomes to that of one centrad. Therefore, the smaller will be the distortions which are observed in scales and operations with such a unity. If n=∞, Z=1 crad. Table 2 shows the angular values in arc degrees (a) and centrads (c) in relation to the respective values of P (prism-diopters), U (angular bi-partition, n=2), and to other derived unities: F (when n=4), T (when n=10), and H (when n=100).
Table 2 Values of angles in arc degrees (a), centrads (c=π.a/1.8), prism-diopters (P=100 tan a), and of the new unities of deviation, U=200 tan (a/2), F=400 tan (a/4), T=1000 tan (a/10), and H=10000 tan (a/100)
| a | c | P | U | F | T | H |
|---|---|---|---|---|---|---|
| 1º | 1.7453 | 1.7455 | 1.7453 | 1.7453 | 1.7453 | 1.7453 |
| 10º | 17.4533 | 17.6327 | 17.4977 | 17.4644 | 17.4551 | 17.4533 |
| 45º | 78.5398 | 100.0000 | 82.8427 | 79.5649 | 78.7017 | 78.5414 |
| 90º | 157.0796 | ∞ | 200.0000 | 165.6854 | 158.3844 | 157.0926 |
| 135º | 235.6194 | -100.0000 | 482.8427 | 267.2715 | 240.0788 | 235.6631 |
| 180º | 314.1593 | 0 | ∞ | 400.0000 | 324.9197 | 314.2627 |
Note that with the assumption of an H value (n=100), the error for H/c when the angle reaches 90º is only 0.00823%, and when it reaches 180º is only 0.03291%. This negligible error is evident for almost any arithmetical operation with this unity. For instance, according to the conversion given by a=100 arc tan (H/10000) and by H=10000 tan (a/100), the calculations previously realized become:
10• (=5.730º) × 3 = 17.189º = 30.000·
60• (=34.377º)/2 = 17.189º = 30.000·
18• (=10.313º) + 12· (=6.875º) = 17.189º = 30.000·
50• (=28.648º) - 20· (=11.459º) = 17.189º = 30.000
For higher values the errors are still negligible:
20• (=11.459º) × 4 = 45.837º = 80.002
160• (=91.665º)/2 = 45.833º = 79.995
50• (=28.648º) + 30· (=17.189º) = 45.836º = 80.001
170• (=97.393º) - 90º (=51.565º) = 45.829º = 79.988
Obviously, higher values of n can be used. However, it is possible that a high degree of accuracy for such calculations may not be required, since expressions of eye rotation measurements, or of eye deviations, have no practical or effective meaning if they surpass whole numbers (that is, if decimal figures for measurements in prism-diopters (or analogous unities) are shown(4). Therefore, a much smaller n value may be practical for the study of strabismus and related subjects. For instance, if n=4, the above calculations fall within acceptable approximations (see below). In each line, the value of an angle when expressed in the linear unity (#) is, firstly, converted to the respective value in degrees of an arc (º). The arithmetical operation is then performed, the respective result is then converted back to the angular value with the new unity (#), and the final approximation is then calculated. The last column shows the relative error between this result and that of the initially incorrect arithmetical calculation.
10# (=5.728º) × 3 = 17.185º = 30.050# ≈ 30# = 0.17%
60# (=34.123º)/2 = 17.062º = 29.833# ≈ 30# = 0.59%
18# (=10.306º) + 12# (=6.873º) = 17.180º = 30.041# ≈ 30# = 0.14%
50# (=28.500º) - 20º (=11.450º) = 17.050º = 29.814# ≈ 30# = 0.62%
20# (=11.450º) × 4 = 45.798º = 81.015# ≈ 81# = 1.27%
160# (=87.206º)/2 = 43.603º = 77.033# ≈ 77# = 3.85%
50# (=28.500º) + 30# (=17.157º) = 45.657º = 80.757# ≈ 81# = 0.94%
170# (=92.102º) - 90# (=50.722º) = 41.380º = 73.018# ≈ 73# = 8.73%
Note that the effective differences between the results of the arithmetically simplified operation and the respective correct values (third column), be they absolute or relative (percentage values), only reach important (significant) quantities for operations dealing with very high angular values. These values, however, are uncommon in the clinical practice of strabismus.



 English PDF
English PDF
 Print
Print
 Send this article by email
Send this article by email
 How to cite this article
How to cite this article
 Submit a comment
Submit a comment
 Mendeley
Mendeley
 Scielo
Scielo
 Pocket
Pocket
 Share on Linkedin
Share on Linkedin

