INTRODUCTION
One of the challenges in the management of strabismus is the difficulty in achieving a desired surgical result, and to insure a stable positive outcome once a desired surgical result is realized. In a recent article quoting the European Early vs. Late Infantile Strabismus Surgery Study (ELISSS), the authors pointed out that in some cases, the reoperation rates reached 60-80 %(1).
Adequate correction of the binocular misalignments depends on several factors. The first is a good diagnosis of the defect, which requires a detailed clinical examination and the capability to correctly interpret the collected data. Examples of diagnostic errors include unobserved muscular dysfunction and an association between the vertical and horizontal deviations, or the "V" pattern. A second factor is the surgical planning, which require a deep knowledge of the theme and excellent strategic experience necessary to relate the diagnostic findings to the expected surgical outcome. Poor selection of the extraocular muscles to be operated on or procedures to be performed on each muscle leads to undesired outcomes. The third factor is the surgery itself. It demands careful execution, which include the use of appropriate instruments, techniques, and procedures, as f as the surgical changes of the immediate results (by the "adjustment of sutures"), are advocated to obtain the desired results.
However, even a proper diagnosis of the oculomotor unbalance, correct surgical planning, and execution do not guarantee the expected results. In many cases, a recurrence of the deviation or the emergence of a "secondary" deviation (in an opposite sense to that of the initial one) occurs after achieving a good surgical correction. This is due to structural and functional adaptations of the oculomotor system to the surgery. It may be due to an error of the innervational stimulus (excessive or insufficient), or due to an error in the response of the extraocular muscles as a reaction to the recessions of their insertions (procedures for weakening the excessive muscular tensions), or due to the resections (stretching procedures), be it of a sensorial readjustment of the binocular status (due to a previous abnormal visual correspondence). The human extraocular muscles have sensory organs, muscle spindles and tendon sensors, which respond to changes in the muscle force and length(2). Sarcomeres adjust their length according to the post-surgery muscle length(3,4). However, the ocular drift caused by muscle underactivity or overactions (by defects of innervation or by defects of muscular response) that force the eye to an undesired position may be of high magnitude. It may occur quickly (in weeks) or very slowly (in months or years).
How to avoid it? It appears quite clear that the simplest possibility would be of a better comprehension of the causes of the misleading issues. This is has been the subject of extensive studies in the recent years. However, although diagnostic and surgical methods have improved, the precise mechanisms responsible for the drift remain unknown. The number of variables involved is so large that the possible suitable formulations to compensate the causes of the drift would be complexes. An alternative solution would be to compensate for the consequences of the phenomenon - to cancel the drift itself. Cancelation of the drift corresponds to creating opposite forces.
RATIONALE
Application of a force causes displacement of the body (unless a force of equal magnitude acts in the opposite direction), that is, a movement is an expression of an applied force. Spacial displacements can be rotational or translational, according to their movement around a fixed or movable point (the centre of rotation, which may be internal or external to the body). Natural eye movements are initiated by the contraction of one or more extraocular muscles. As a consequence of the shape of the eye (approximately spherical) and the existence of surrounding structures that confine the eye (the orbit and its contents), almost all of the forces originating from the muscular contractions results in an ocular rotation. A simultaneous relaxation of one or more antagonistic muscles, according to the Sherrington's law, also occurs, resulting in a smooth ocular rotation (Figure 1).
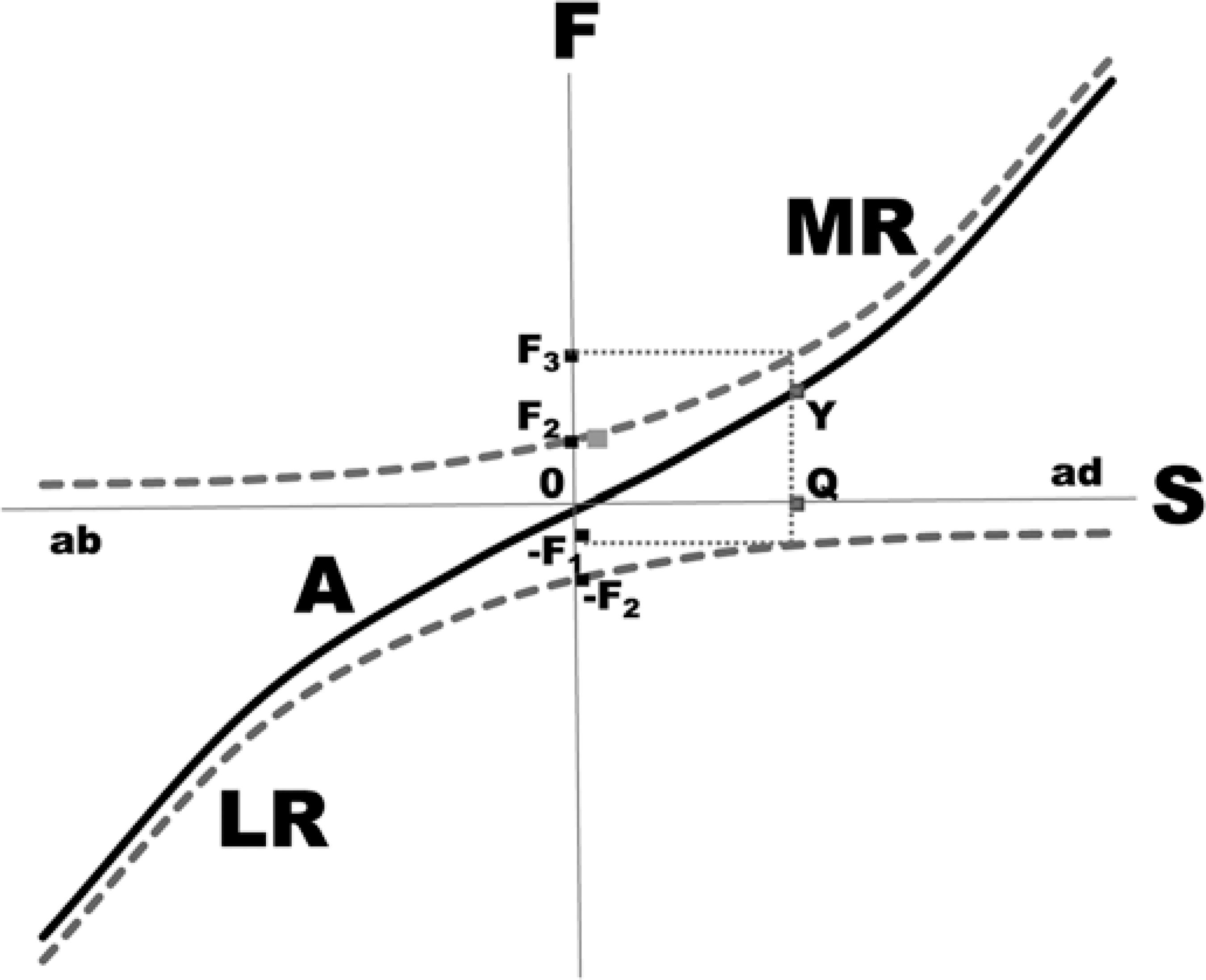
Figure 1 Schematic representation of the active (innervationally induced) forces (F, ordinates) and eye positions (S, abscissas) of the medial rectus (MR) and of the lateral rectus (LR), the length-tension curves, and the respective resultant (A). For the movement from the primary-position (0) to an adduction Q, the force of the medial rectus increases from F2 to F3 (contraction), while that of the lateral rectus decreases from -F2 to -F1 (relaxation). As F2 + (-F2) = 0 (the tonic forces of the medial rectus and that of the lateral rectus balance each other in the primary position of the gaze), the net result is a force (F3 - F2) + [-F1 - (-F2)] = F3 - F1 = YQ. Note that the sign of addition between the forces of the medial rectus (F3 - F2) and that of the lateral rectus (F1 - F2) means that both muscles contribute to the normal adduction (Sherrington's law).
The theory also establishes that continuous application of a force on a body causes acceleration, and once the force is removed, the motion (rotational or translational) is continued at a constant speed. However, this does not occur in the eye since multiple forces that act in the opposite direction (friction, viscosity, as well as resistive forces originating from the "passive"stretching of the elastic structures such as conjunctiva, fascias, and the extraocular muscles) forces a deceleration, eventually stopping the motion (Figure 2). Some of these forces (passive forces) are accumulated by the stretched structures and may be subsequently recovered. In other words, the "passive" forces are of fundamental importance in ocular movements since their magnitude rises to a value that balances the "active" forces (developed by the muscular contractions and corresponding relaxations) to stop an initiated ocular rotation(5,6) (Figure 3).
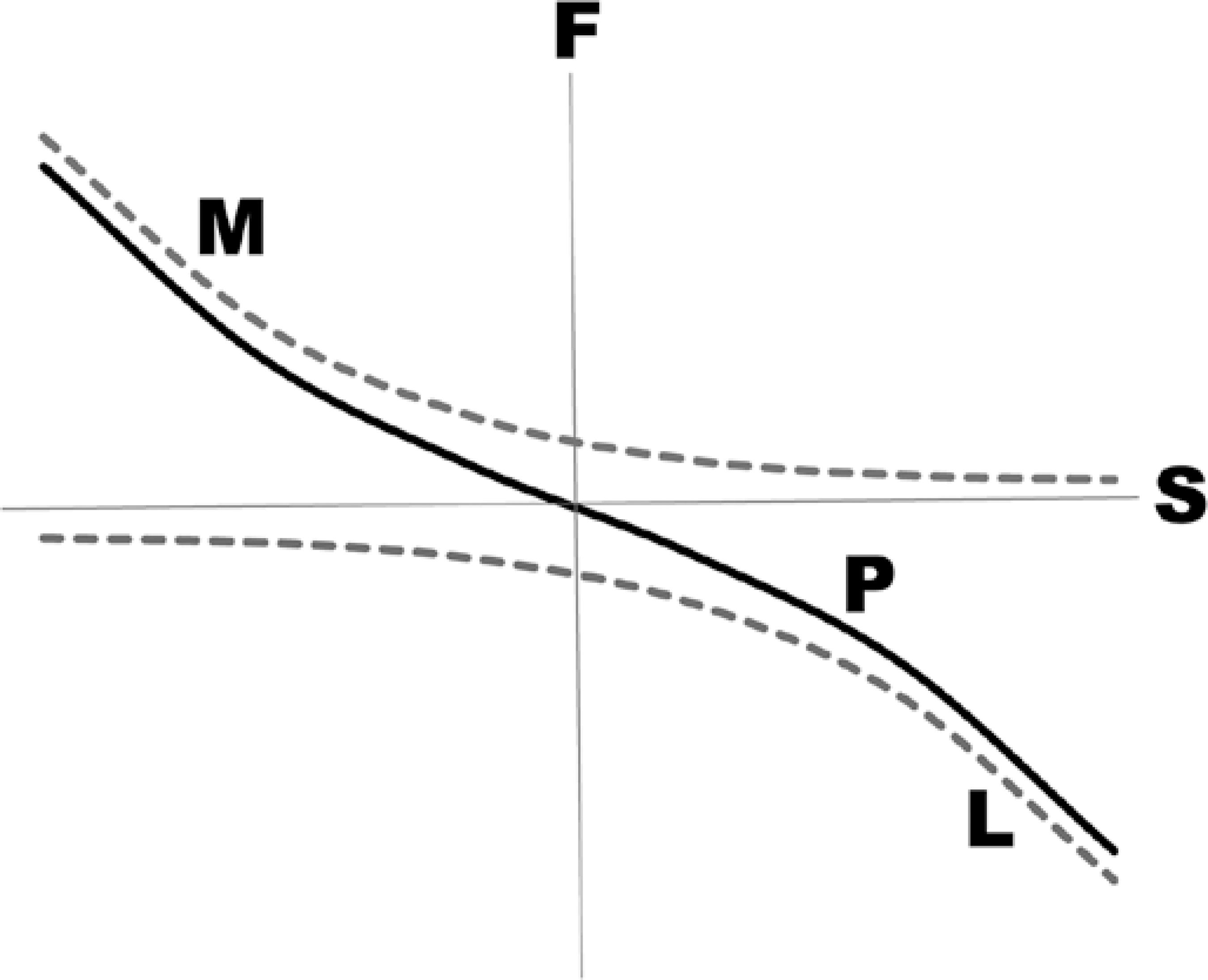
Figure 2 Schematic representation of the passive (or reactional, or restrictive) forces (F, ordinates) and eye positions (S, abscissas) of the medial (M) and of the lateral (L) periocular tissues of the eye and the respective resultant (P).
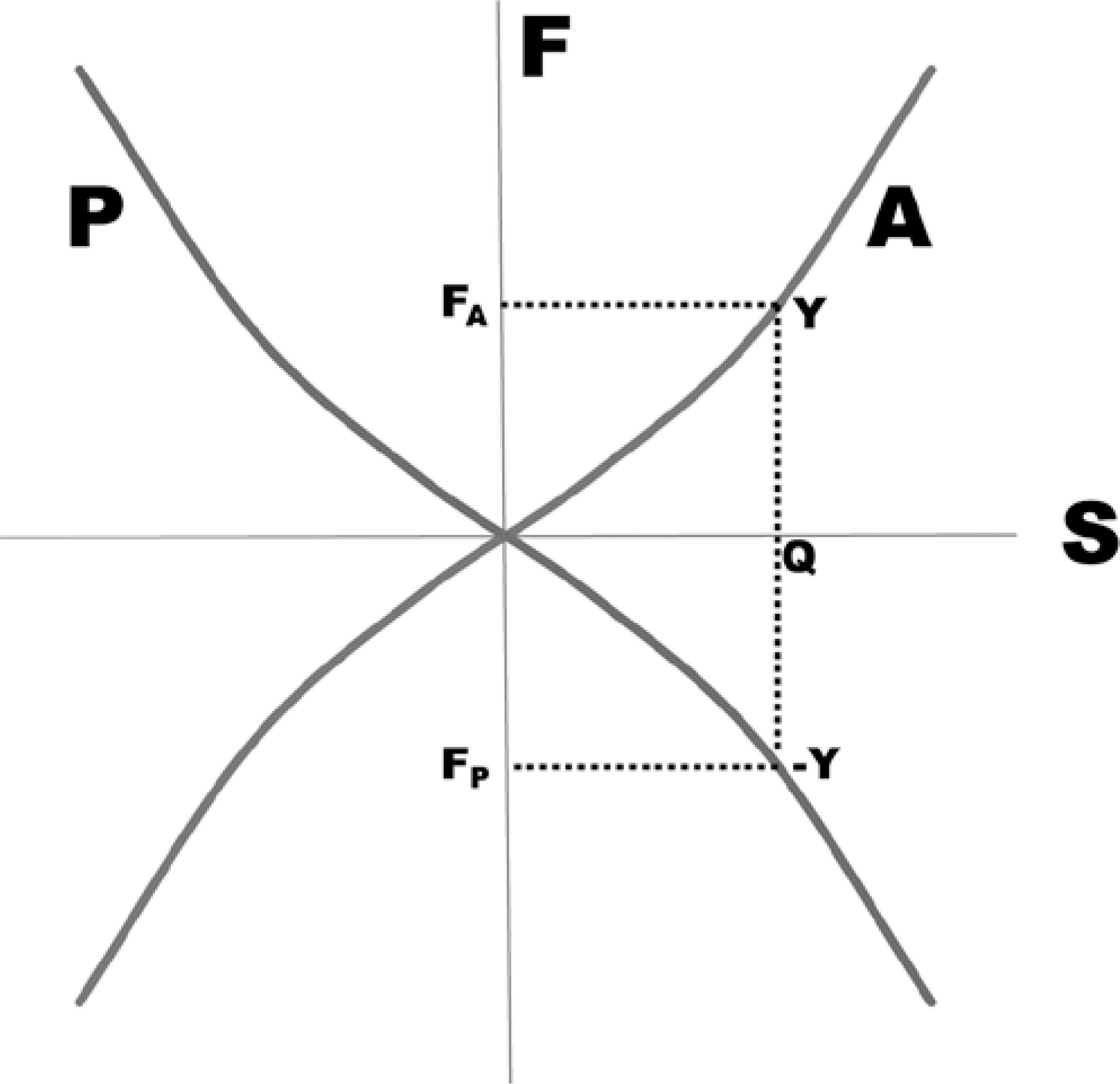
Figure 3 Schematic representation of the resultant of the active forces (A) and that of the passive forces (P). The movement of the eye subjected to an active force FA = YQ (see Figure 1) stops at the position Q because the passive forces amounts to the same value in magnitude, but with an opposite sign (FP = -YQ). Note that the resultant of the passive forces (P) is represented by a mirror image of the resultant of the active forces (A).
The forces generated are a consequence of the neural stimuli that triggers muscular contraction and relaxation. They evoke ocular rotations, during which the kinetic energy is stored as potential energy in the elastic structures of the eye and the orbit. An increment of innervation may be voluntarily dispensed to increase the magnitude of an ocular rotation. But if the system conserved the energy once a force is generated, it would be entirely conserved and the eye would move from one side to the other like a pendulum (harmonic oscillation). However, in the eye, an important part of the generated energy is lost in the forms of inelastic deformations of the periocular structures and heat (caused by the friction between the moving surfaces). Therefore, it can be said that the innervations are spent to overcome the dissipative force of the ocular mechanical system (Figures 4 and 5). The magnitude of the dissipative forces (the width of the strip between the dotted lines parallel to the axis S in Figure 5) could be increased to correct the oculomotor imbalance.
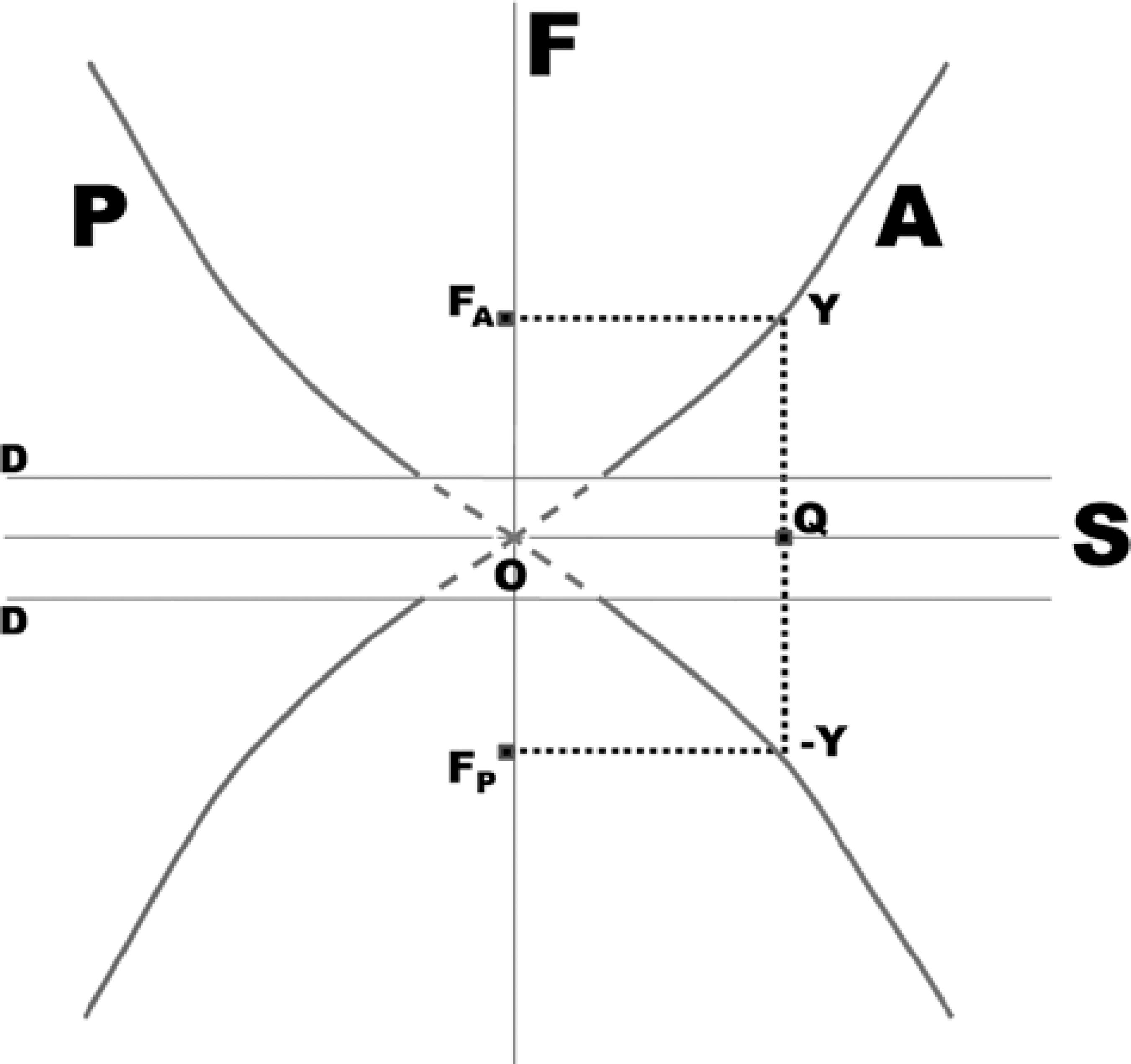
Figure 4 Schematic representation of the active (A), passive (P), and dissipative (D) forces. Dissipative forces are supposed to have a constant value, but oppose a given rotation. If active (or passive) forces evoke adduction, either from the temporal side to the primary position (centripetal adduction) or from the primary position to the nasal side (centrifugal adduction), the dissipative forces appear to neutralize them. Therefore to reach a point Q from the primary position of gaze (0), the active force required is D + FA, that is, a component D is lost, while FA is spent to stretch the elastic periocular tissues (an energy which can be recovered), so that the corresponding point to Q cannot be Y (see Figures 5 and 6).
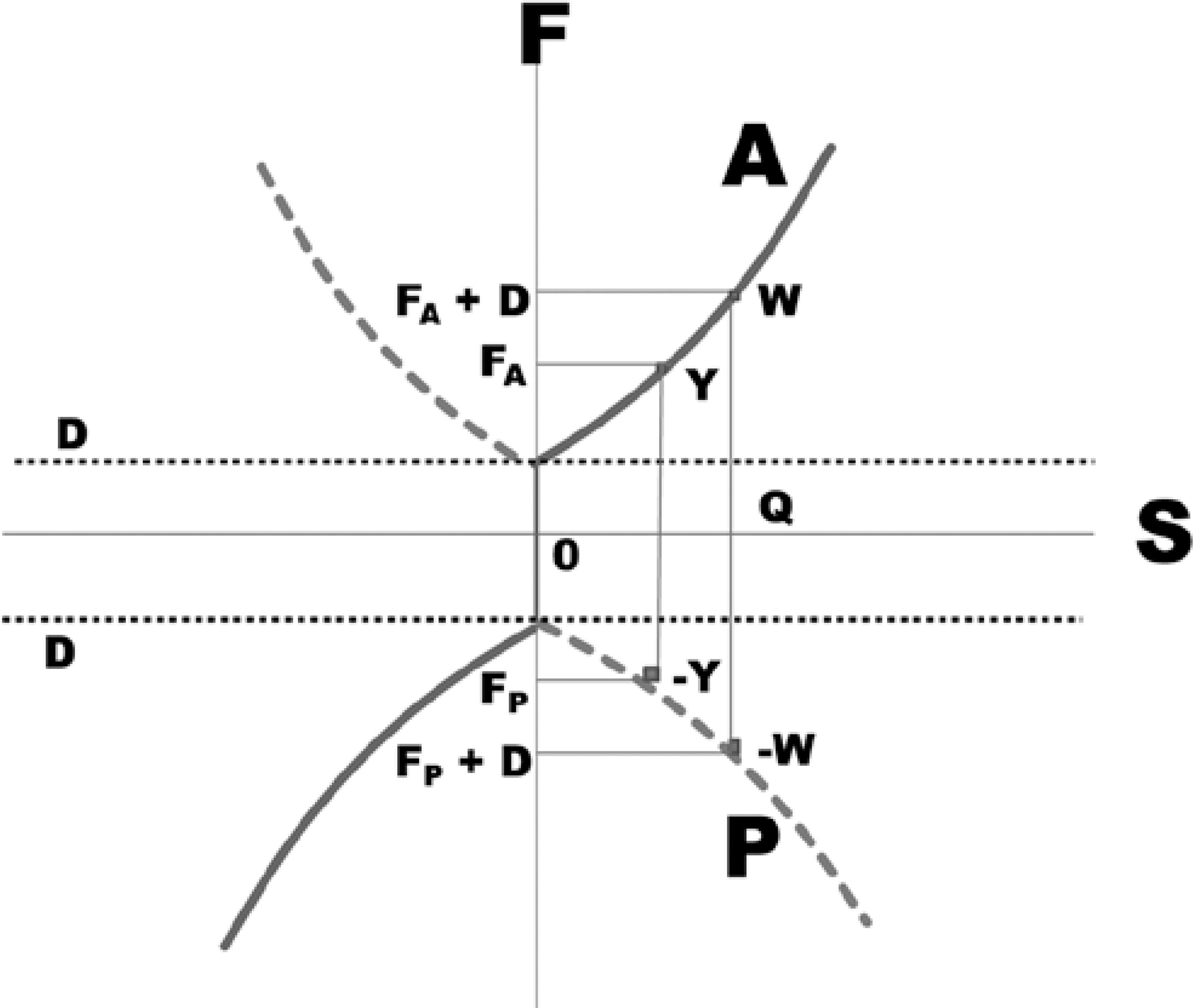
Figure 5 Resultant of a combination of representative lines of active (A), passive (P), and dissipative (D) forces. As the initial active force (applied from the primary position of gaze, 0) is spent to overcome the starting friction, the ocular movement is produced only after a value D is surpassed. From this point, increments of active forces are opposed by the passive forces from the elastic periocular tissues, thereby accumulating energy. Therefore, the force required to move the eye to the point Q is greater (FA + D), as if the curve of the first quadrant were displaced to the center, to the axis of the ordinates. This also occurs to the curves of the other quadrants. Therefore W is a point of a greater force (FA + D) than Y (force FA).
The magnitude of the active and passive forces responsible for normal ocular rotations have been determined. However, a direct measurement of the forces implicated in the post-surgery eye drift has not been reported. These forces may be indirectly estimated from the respective ratios of the mechanical effects related to the ocular drift and to a normal (pursuit or saccadic) eye movement.
Let us assume an ocular drift corresponding to a deviation of θ = 20º (approximately 36 prism-diopters), lasting for a time (t) of 4.107 seconds (approximately 15 months). The average angular velocity (w) of such a drift is,
Compared to such a speed, an eye rotation with the angular velocity of 50º/s (the normal velocity of a smooth pursuit movement is about 30º to 50 º/s, although higher values of 100 º/s may be registered)(7) is approximately one hundred million (100×106 = 108) times faster. A saccadic movement with a peak angular velocity of about 500 º/s (it may be even greater) is approximately one billion (109) times faster than a drift.
In a rotating body, where the motion starts from the rest as in the case of ocular drift, pursuit movement, or the saccadic movement, the work done to produce the rotation appears as kinetic energy. The kinetic energy (Ek) of the respective movements is:
where I is the moment of inertia of the eye. The moment of inertia of a body expresses its resistance to any change of its state of rest or of motion and, therefore, is related to its mass (m). In conditions where friction and other resistive forces are absent, the moment of inertia of the eye will be constant (I = k×m), so that for the ocular drift, pursuit movement, and saccades, the ratio of the kinetic energy of two of such motions will be proportional to the square of their velocities. i.e.,
Thus, the kinetic energy of the drift might be 10 quadrillionths of that of a normal ocular pursuit movement or one quintillionth of that of a saccade.
Note that, according to the expression given below, the kinetic energy related to each of these motions is directly proportional to the respective total work (W), torque (T), and applied force (F).
Consequently, the respective ratios of two of these variables, in each two of the considered motions, figures as shown to the comparisons of the kinetic energies, on the order of magnitude of quadrillionths to quintillionths. To have an idea of such a proportion, that is the same as between the diameter of a red blood cell (10-5 m) and the distance from Neptune (the farthest planet of our star system) to the Sun (1013 m); or between the mass of a red blood cell (10-13 kg) and of a body weighing 100 tons (105 kg).
Another mechanical variable is the power (P), which is also directly related to the velocity according to the following expression:
In this case, the ratio of powers is,
A mechanical force (or energy, work, power, etc.) acting on a body, but not neutralized by an opposing force, produces a continuous motion. However, this is not applicable in the case of ocular movements since friction, viscosity, and other forces resisting the ocular movements simultaneously act on the eye. The magnitude of friction (or viscosity) is different for movements with different speeds. For instance, the starting friction (that prevents the initial motion) is greater than the sliding friction (that acts after the motion is initiated). Therefore, since it acts persistently (permanently or intermittently), a mechanical factor of a very small magnitude could cause a large ocular drift of the order of many degrees. For instance, even when subjected to a small force, a ball may roll to a large distance in an inclined plane, but may resist to the displacement if the friction against the plane increases, or may tend to return to a specific position if placed at the bottom of a curvilinear plane. Similarly, a drop of a fluid may be prevented from falling if its viscosity is increased. Therefore, even if correct estimates of the absolute values of the mechanical properties of the ocular drift are not available, the respective ratios between them and those of faster ocular movements would probably remain showing very large differences between them.
In summary, one should expect that the addition of continuously acting forces, although small in magnitudes, in the opposite direction of those that cause the undesired ocular drifts after the corrective surgeries for strabismus, might be sufficient to prevent the drifts.
METHODS
General considerations
Conventional modes
Several methods can be used to add rotational forces to the oculomotor system. One such method is the traditional reinforcement of muscles (or by the weakening their antagonists) or the manipulation of the non-innervated tissues (conjunctiva, etc.) using classical surgical procedures. (Muscular recessions, muscular resections, or their combinations do not significantly change the absolute value of the muscular forces since such procedures may be understood as simple adjustments of the respective muscles to a new eye position. The changes in ocular positions related to specific levels of innervation might be alternatively interpreted as respective changes in forces)(8,9). However, since it is assumed that the appropriate surgery was planned and executed, this method cannot be adopted. In the same sense, the immediate adjustment of the ocular positions cannot be assumed also as an ultimate solution to avoid late undesired results (under or overcorrections of the strabismus). Even when adjustable sutures are used, the incidence of an unsuccessful outcome is sometimes high, not different of surgeries without additional procedures(10-12).
Variations of convergence by means of, a) the accommodation (increased convergence by increased accommodation produced by plus minus lenses or by decreasing the value of needed positive ones; or decreased convergence, by the opposite procedures) and/or b) facilitation of binocularly fusional mechanisms (by prisms) are a possible and common methods, but limited by several factors and with a relatively small range of correction. The effect is also temporally limited by the conditions of use of such aids.
Other possibilities
Through the periocular injection of viscous substances, studies have attempted to increase the passive, restraining forces to the ocular rotations (by means of increasing the friction)(13-15). Although an increase in the periocular viscosity may reduce the angular velocity of the eye to the same applied force, it may not produce the required adjustment for a specific (desired) eye position, the establishment of a fixed direction around which the oculomotor balance must occur (e.g., the so-called primary position of gaze).
In contrast, the forces of magnetic fields could make possible adjustments in the eye position at which a stabilization might be required(16). Additionally, as has been shown in the control of nystagmus, magnetic fields allow the annulment of undesired eye movements(17). The forces of a magnetic field act statically as imaginary lines of suture between the sclera and the orbit, where the elements of the magnetic circuit are fixed. The net mechanical effect is resistance against an ocular movement, mimicking an increase in the dissipative forces (Figures 4 and 5). Similar to tiny sutures being broken by an ocular movement caused by greater rotational forces, the magnetic attraction between the elements of the circuit decreases exponentially with the eye movement(16,17) and the magnetic elements may be drawn away. The advantage of such magnetic ties over mechanical sutures is that the amplitude of the magnetic links will be automatically and fully restored once the original conjunction is re-established.
Forces of magnetic fields
The magnetic forces are due to magnetic fields. A magnetic field is generated when an electric current passes through a conducting wire. Alternatively, the magnetic forces may exist as part of the inherent physical property of some materials (permanent magnets). In a magnetic field, the matter behaves in three fundamental ways, two of which are of little practical interest, because the interaction is considered weak. One is a weak repulsion to the lines of field (diamagnetic substances). The second is a weak attraction (paramagnetic substances), and the third is a substantial attraction to such lines (ferromagnetic substances). Ferromagnetic substances may even retain the magnetic lines of a generated field and act as magnetic "suppliers" (permanent magnets). Therefore, for a magnetic circuit to occur, the magnetic field has to be provided either by a permanent magnet or by an electric current (electro-magnets), while the other element (through which the lines of field pass, closing the circuit) may be a piece of a ferromagnetic substance. Although the use of an electro-magnet may allow for regulating the intensity of the generated forces, the magnetic fields of permanent magnets represent a more practical solution.
A permanent magnet is characterized by two key properties, namely the intensity ("strength") of the generated field (H) and the density of the magnetic flux (or intensity of magnetization, or magnetic induction, (B). Since the unit of H is N (newton)/weber (or praoesterd) and that of B is weber/m2 (or tesla), the product B.H is expressed in N/m2 or force (N) per unit area (m2), an equivalent of the mechanical entity pressure (The unit N/m2 is called "pascal", Pa, 1 N/m2 = 1 Pa = 10 baryes = 10 dyn/cm2 ≈ 104 gf/cm2 = 100 gf/mm2). Note that the effectiveness of a magnet is expressed by B.H in MGOe (mega gauss-oersteds, which is equivalent to 0.1 Pa ≈ 10 gf/mm2) units. In other words, the action of a permanent magnet fixed to the orbit can be understood as the application of a pressure over the piece of the magnetic material fixed to the ocular surface (hence the value of the concept of the B.H product), increasing the "friction" between the two parts. By analogy, this is similar to the difficulty of sliding a chair in which a person is seated (the increase in pressure due to the weight of the person increases the friction between the chair and the floor). The action (forces, "pressure") of a magnetic field decreases greatly with a small increase in the distance between the elements of the circuit.
Therefore, the magnetic forces are proportional to the amount of the magnetic flux (B) originating from the magnet and to the intensity of the field (H), which is a function of the area (or the volume) of the magnet. A larger magnet of a lower power will generate a net force equivalent to that of a smaller magnet of a higher power.
Structure of possible magnetic circuits
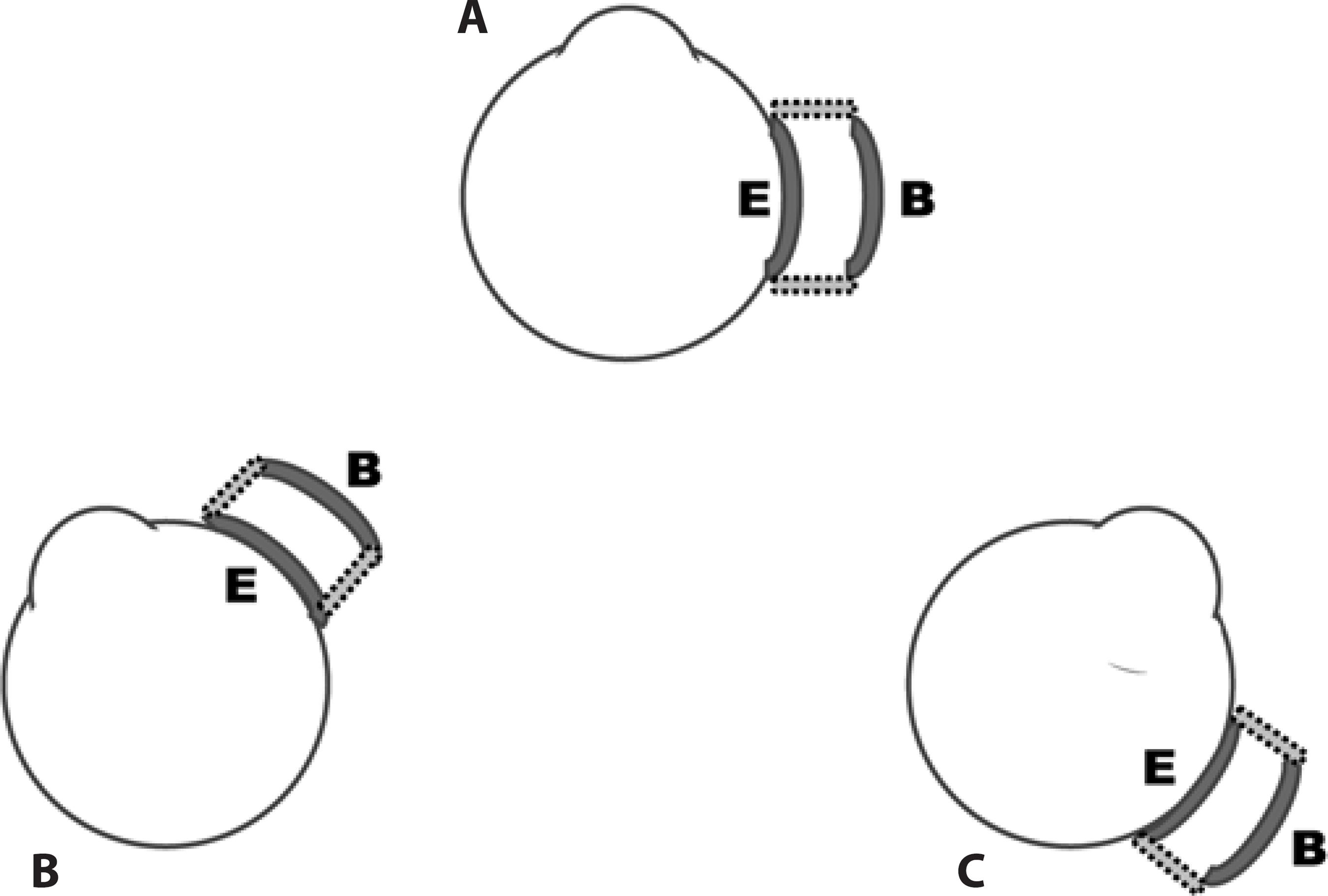
Depending on the size of the metallic piece (or magnet) fastened to the eye and the magnet (or the metallic piece) that is tightened to the orbit, four basic models can be used to build a magnetic circuit for generating the forces that stabilize the oculomotor system (Figure 6).
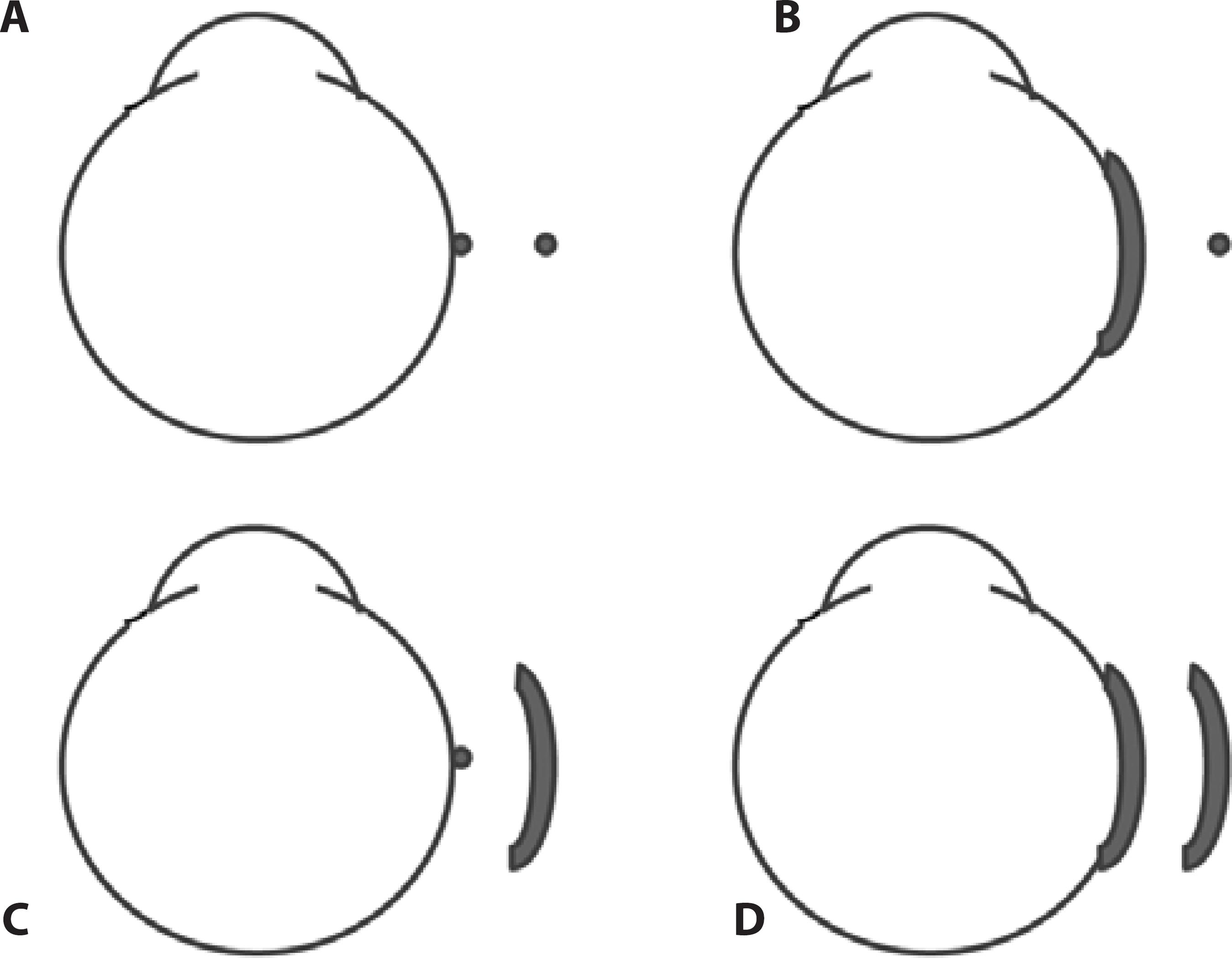
Figure 6 Schematic representation of the possible relative sizes of the elements of a magnetic circuit adapted to introduce forces to the oculomotor system. A) Elements of a minimum size. B) An element of a greater size fastened to the eye and an element of a very small size fixed to the orbit. C) An element of a small size fastened to the eye and an element of a greater size to the orbit. D) Both elements of greater size.
The position where each of the elements of the magnetic circuit (permanent magnet and the ferromagnetic material) is fixed (to the orbit or to the eye) is alternatively indifferent by the mechanical viewpoint. For practical reasons (the difficulty of shaping the permanent magnets), it is easier to fix the permanent magnet to the orbit (or externally to it) and the ferromagnetic material to the eye. Previous studies have shown that small pieces of steel fixed to the eye produce only an initial inflammatory response(18-21) and could bear external tractions of up 80 gf(18,20).
At first glance, it would appear that small elements fastened to the eye and to the orbit (Figure 6 A) would be preferable. However, when the elements of the magnetic circuit are very small, the system would work as if only the starting friction increased (the weakening forces between the elements of the magnetic circuit when they become more distant may be neglected).
One of the possible disadvantages of such a design is that once the eye moves with its magnetic element fixed to it, the distance between this an element and the element fastened to the orbit increases, causing an exponential drop in the magnetic force between these elements. Although the magnetic forces between the elements fixed to the eye and that fixed to the orbit will still be present, such a force will be insufficient to neutralize an acting muscular force (as in nystagmus) at the new ocular position. However, if one of the elements (or both) covers a greater area, the stabilizing forces will continue to act maximally while the magnetic points are facing each other (Figure 7). Therefore, in such a condition, in spite of the eye movement, a nystagmus may be neutralized at the end of the rotation (in a new ocular position and at the intermediate ones). The result will be as if, in addition to the starting friction, a sliding friction is also introduced (Figure 7).
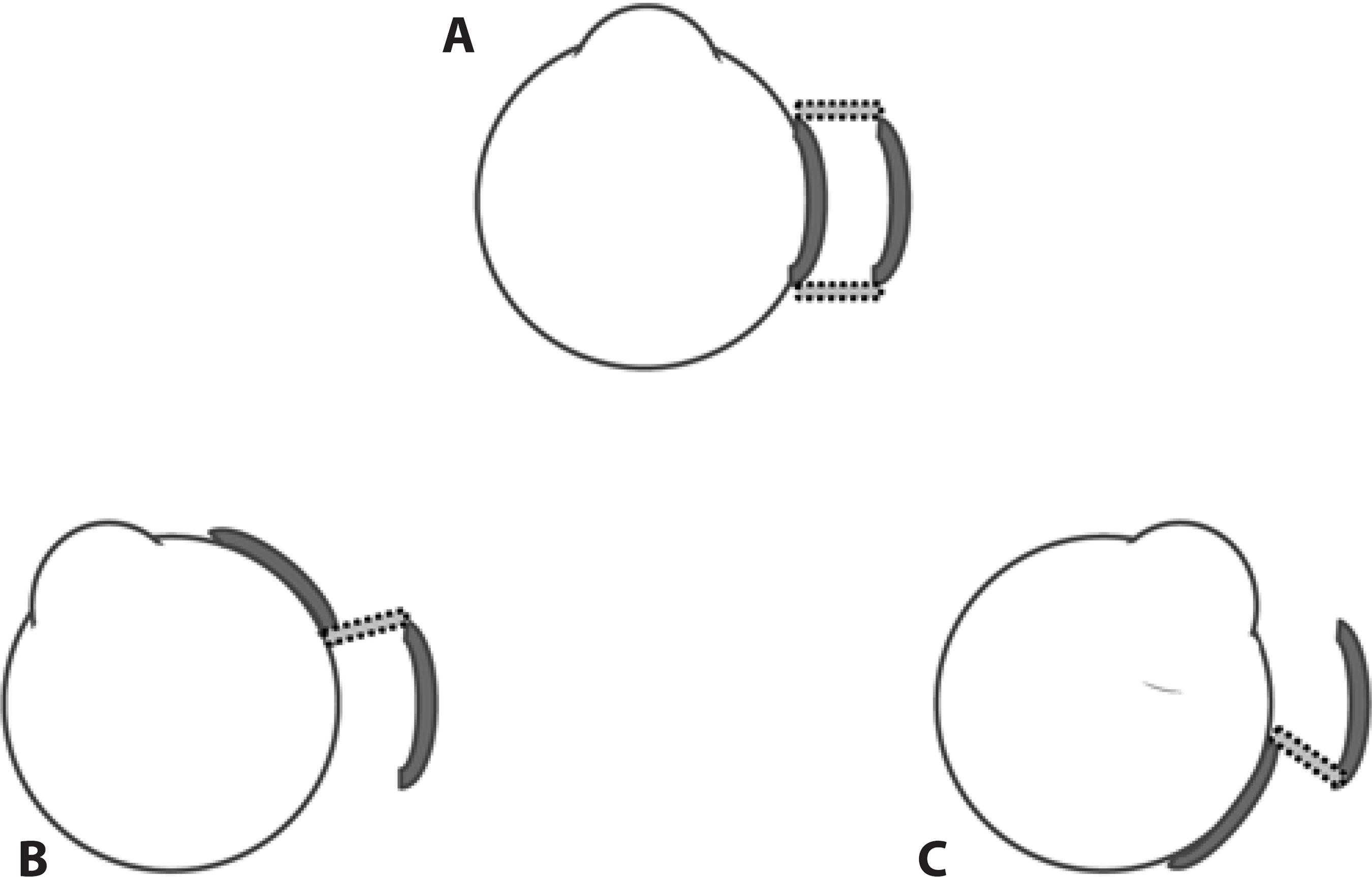
Figure 7 A) From the primary position of gaze, ocular rotations to the left. B) And to the right. C) Could be made more difficult by the action of magnetic (restraining) forces, if at least some parts of the elements of the magnetic circuit are kept close, facing each other (although partially).
An ancillary problem of the punctual element fixed to the eye (Figures 6 A and 6 C) is that the maximum force generated by the magnetic element is applied to a small area of the ocular surface, so that the pressure on the surface may reach a very high magnitude. Therefore, the constructions shown in figures 6 b and 6 d appear to be safer to the eye.
Another advantage of using the magnetic forces is the possibility that the eye position can be finetuned by adjusting the relative positions of the elements in the magnetic circuit(16). The element that is not fixed to the eye should be chosen for such eventual displacements (Figure 8). Note that the eye may not move simultaneously with the displacement of the orbital element of the magnetic circuit. This would only occur if the "tying" lines (proportional to the intensity and density of flux of the magnetic field) are strong enough to pull the eye to the new position of balance. This possibility (use of magnetic fields with forces strong enough to pull the eye) can be tapped to produce ocular movements and to restore the lost ocular rotations in cases of paralyses(22-25).
DISCUSSION
The effects of continuous action of a weak magnetic field on the retina, lens, or other ocular structures have not been studied. Living organisms are immune to terrestrial magnetic field (approximately 30 to 60 microteslas or 0.3 to 0.6 gauss, depending on the geographic location). Humans are continuously being permeated by other magnetic fields generated by direct electric currents without any reported adverse effects or consequences. Such effects of the permanent magnets or electro-magnets placed close to the eye can be neglected, particularly because the magnetic field will be confined to the elements of the circuit. In other words, if a magnetic circuit is properly adjusted with reference to (a) the intensities of field and flux of the permanent magnet in one side, and (b) to the size and magnetic permeability of the ferromagnetic "shield" in the other side, a leakage of the magnetic field is not expected(16,17). Therefore, an effect of the magnetic field on ocular structures also need not be expected.
The permanent magnets and ferromagnetic pieces fixed to the orbit and/or to the ocular surface may impose some limitations such as rendering the MRI examinations of the subject impossible. Whether a small magnetic film fixed outside the orbit and miniscule amounts of ferromagnetic material placed at the ocular surface for stabilizing the eye position after a corrective surgery of strabismus would be harmful to the eye under in the presence of a strong magnetic field is not known.



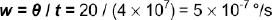
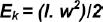
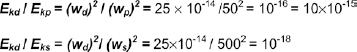
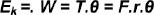
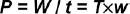
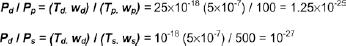
 English PDF
English PDF
 Print
Print
 Send this article by email
Send this article by email
 How to cite this article
How to cite this article
 Submit a comment
Submit a comment
 Mendeley
Mendeley
 Scielo
Scielo
 Pocket
Pocket
 Share on Linkedin
Share on Linkedin

