RESUMO

A acuidade visual representa o inverso do ângulo visual, ou seja, da menor distância angular entre dois pontos que podem ser vistos como separados. Apesar de ser a medida da função visual mais comum na prática oftalmológica, é muitas vezes interpretada erroneamente, principalmente devido às inúmeras tabelas e diferentes sistemas de notações empregados na clínica. Este artigo revisa alguns conceitos sobre a quantificação da acuidade visual, suas principais notações e tabelas de medida, discutindo as vantagens do uso da escala logarítmica.

Descritores: Acuidade visual; Optometria

ABSTRACT

Visual acuity represents the visual angle or the smallest distance between two points that allows their discrimination as separated points. Although it is the most common clinical measurement of visual function, it is often misunderstood, especially due to the variety of charts and different notation systems employed for its quantification. This article reviews some concepts about visual acuity measurement, the main notation systems, type of charts and discuss the advantages of using logarithmic scales.

Keywords: Visual acuity; Optometry

---

 

 

INTRODUÇÃO

A medida da acuidade visual é a principal ferramenta clínica para a avaliação funcional da visão. Nesse sentido, o uso de tabelas de acuidade visual é, sem dúvida, a prática mais comum do exame oftalmológico.

Apesar de largamente utilizada, a terminologia empregada para nomear as diferentes tabelas usadas na clínica é imprecisa e confusa. Por exemplo, é comum referir-se a tabelas de "Snellen" sem que se saiba exatamente o que isso significa. O problema aumentou com o grande número de publicações que sugerem que as tabelas com escalas logMAR (logaritmo do ângulo mínimo de resolução) sejam as mais adequadas para trabalhos clínicos de seguimento de acuidade visual ou mesmo levantamentos populacionais de acuidade visual⁽¹⁾.

O presente trabalho pretende discutir de maneira clara e simples os conceitos subjacentes à construção de tabelas logarítmicas de acuidade visual, de modo que qualquer oftalmologista seja capaz de confeccionar, com a ajuda de uma gráfica comercial, tabelas padronizadas para trabalhos científicos e prática clínica.

Definição de acuidade visual

Acuidade visual, por definição, é o inverso do ângulo visual limiar em minutos de arco (α). Limiar é um termo usado em vários campos do conhecimento, muito comum em estudos psicofísicos, para denotar a menor quantidade de estímulo capaz de gerar uma resposta. No caso da acuidade visual, o limiar é o menor ângulo que permite a discriminação de dois pontos como separados⁽²⁾. Arbitrariamente, o ângulo visual de 1' (lê-se um minuto de arco) foi determinado como acuidade visual padrão. Todavia, apesar desse ângulo visual aproximar-se mediado limiar de pessoas saudáveis com aproximadamente 60 anos de idade, ele não é o menor ângulo de resolução do olho humano, que é estimado teoricamente em 0,75' para pupila de 4 mm de diâmetro⁽³⁾.

Notações de acuidade visual

Sem entrar no mérito de qual notação é a mais apropriada para designar acuidade visual no Brasil, assunto já discutido apaixonadamente nos Arquivos Brasileiros de Oftalmologia⁽⁴⁾, sempre que se inverte qualquer valor de acuidade visual obtém-se o ângulo visual.

As principais notações utilizadas atualmente são: a decimal, a fração de Snellen, a frequência espacial e o logaritmo do ângulo visual.

A notação decimal é obtida tomando-se o inverso do ângulo visual. Por exemplo, quando acuidade visual é igual a 0,2, o α é igual a 1/0,2 = 5'. A fração de Snellen exprime a mesma relação da notação decimal por meio de uma fração cujos termos podem estar em pés (principal unidade de medida de comprimento nos Estados Unidos) ou em metros (unidade de medida de comprimento do sistema internacional). Originalmente, o numerador da fração representava a distância entre o paciente e o quadro de medidas e o denominador a distância em que o teste resultaria em ângulo de 1 minuto de arco. Todavia, essas frações são usadas para qualquer distância de medida, ou seja, a acuidade visual notada como 20/70 é muitas vezes medida a quatro metros de distância (o que não corresponde a 20 pés ≈ 6 metros). Vale ressaltar que a notação não está totalmente errada, pois denota o ângulo visual correto, mas foi usada inapropriadamente.

A notação ciclos/grau (C/º) é usada preferencialmente para designar a acuidade visual medida com redes quadradas. Nesse caso, em uma rede de barras pretas e brancas alternadas, um ciclo é composto por duas barras, e 1 grau é composto por 60 minutos de arco. Assim, para a acuidade de 1 C/º temos um ângulo visual de 30 minutos de arco. Transformando para as outras notações: acuidade visual = 0,03 ou 20/600 ou 6/180, e acuidade visual de 30 C/º seria o equivalente ao ângulo de 1', 1,0 decimal, ou 20/20, ou 6/6.

Finalmente, chegamos ao logaritmo do ângulo visual. O logaritmo de um determinado valor é o expoente que, elevado a uma base, resulta nesse valor. Por exemplo, na base 10 o log1 = 0 visto que 10º = 1. Outros exemplos: log10 = 1 e o log 100 = 2, pois 10¹ = 10 e 10² = 100.

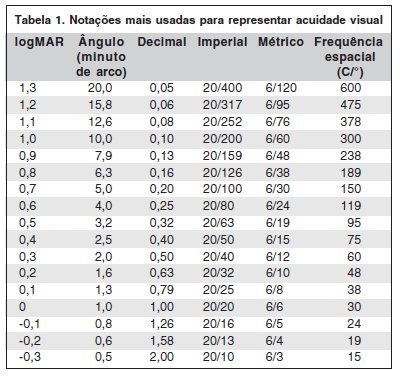
A tabela 1 relaciona a correspondência entre os diferentes sistemas de notação de acuidade visual. Notar que é absolutamente irrelevante optar-se pela notação a ou b. O importante é o instrumento de medida, ou seja, as tabelas de acuidade visual. Antes de se discutir como as tabelas são construídas, é preciso uma breve noção sobre o conceito de escala.

 

 

Escalas

Quando se estuda a variação, ou o intervalo de valores de determinada grandeza em determinada escala, a primeira questão que se coloca é como esses valores são distribuídos. O termo escala diz respeito à natureza de distribuição de uma determinada variação. Por exemplo: 1, 2, 3, 4, 5... etc. é uma série de progressão aritmética e tem variação conhecida, igual a 1 entre seus valores. A série de Leonardo de Pisa, também conhecida como série de Fibonacci, 1, 1, 2, 3, 5, 8, 13... etc., é caracterizada pelo fato que o terceiro termo é sempre a soma dos dois precedentes, ou seja 5 = 2 + 3, 8 = 5 + 3, e está associada a muitas curiosidades, como a proporção áurea (razão entre um termo e seu antecessor, que converge para 1,618 quanto maior for esse valor). Esse número foi frequentemente utilizado em pinturas renascentistas e pode ser encontrado na proporção de conchas (o nautilus, por exemplo) e em seres humanos (relação entre o tamanho das falanges).

Outra possibilidade seria: 2, 4, 8, 16, 32 etc. Nota-se que o intervalo entre os termos é desigual, porém a razão entre eles é constante igual a 2, já que 4/2 = 8/4 = 16/8. Esse tipo de escala, na qual a razão entre os termos é constante, é denominada geométrica. Uma propriedade interessante das séries geométricas é que, quando os seus termos são expressos em logaritmos, a progressão passa a ser aritmética. Por exemplo, na serie supracitada (2, 4, 8, 16, 32), o log de 2 na base 10 é igual a 0,3; o de 4 é igual a 0,6, o de 8 é igual a 0,9 e assim sucessivamente (intervalos de 0,3 em escala logarítmica ou razão entre os termos=2). Essa é a razão das séries geométricas serem também conhecidas como logarítmicas.

Em tempo, se o log na base 10 da razão entre os números de uma série é igual a 0,3 (lê-se 0,3 log = 2) diz-se que houve variação de uma oitava (dobro), enquanto um terço de uma oitava (0,1 log) é igual a 1 decibel. Logo, decibéis e oitavas são sempre variações, ou seja, reduções ou aumentos, e não medidas absolutas.

Fica claro agora que qualquer tabela dita logarítmica tem como elemento fundamental o fato de que o ângulo visual varia geometricamente, ou seja, a razão (e não a diferença) entre os termos é constante.

Tabelas de acuidade visual

Para permitir a medida, uma tabela de acuidade visual deve conter um espectro de valores de ângulos visuais. A figura 1 mostra como diferentes tabelas distribuem esses valores entre as linhas e a figura 2 mostra a distribuição espacial desses valores nas tabelas. Notar a regularidade da tabela logarítmica e a arbitrariedade das demais.

 

 

 

 

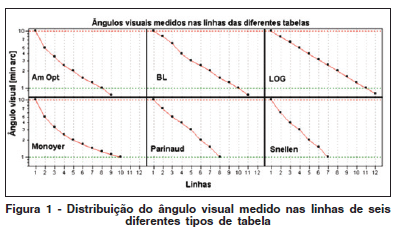
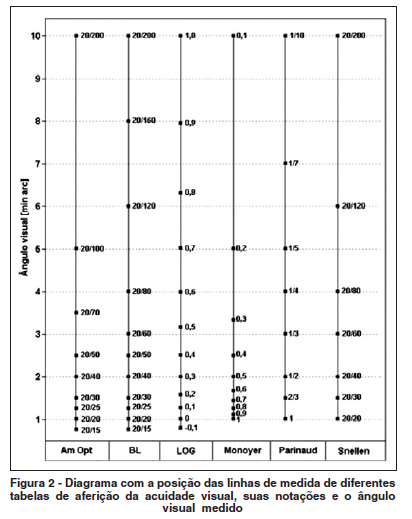
É fácil notar que cada fabricante emprega um tipo de variação próprio e aleatório. Ou seja, na maioria dessas tabelas não há sistematização dos intervalos angulares medidos. Vale ressaltar, que as distâncias entre as linhas e optotipos adjacentes também não apresentam nenhuma relação com o tamanho dos optotipos, o que pode causar discrepâncias nas medidas⁽⁵⁾.

O problema da distribuição aleatória dos valores de acuidade visual na tabela também vem à tona quando examinadores fazem comparações entre acuidades visuais pela linha da tabela na qual ela foi medida (ganho de linhas). Nesse caso, se os intervalos entre a acuidade visual medida nas linhas de uma tabela não forem regulares e constantes, as referências numéricas e operações matemáticas (cálculo de médias, variabilidade e suas relações) podem levar a interpretações errôneas⁽³⁾.

Recomenda-se usar o ângulo visual, ou seu logaritmo (que pode ser obtido diretamente na tabela de medida), para operações matemáticas com a acuidade visual, pois este é o valor quantitativo a ser comparado.

Construção da tabela

A construção das tabelas de medidas tem sido alvo de inúmeros estudos e controvérsias durante os últimos séculos⁽⁶⁾. Três conceitos podem ser considerados os principais consensos que devem ser incorporados na construção de tabelas para medida da acuidade visual:

(1) o aumento do tamanho do optotipo ao longo da tabela deve ser em progressão geométrica com razão de = 0,1 log, ou 1 decibel, ou aproximadamente 1,26, como proposto por Green em 1905⁽⁷⁾;

(2) os optotipos usados devem ter legibilidade similar⁽⁸⁾.

(3) espaçamentos entre as linhas devem ser iguais ao tamanho do optotipo da linha inferior⁽⁵⁾.

Os primeiros a idealizar uma tabela de medida da acuidade visual que visava satisfazer esses critérios foram Bailey e Lovie em 1976⁽⁹⁾, que foi a principal base para o desenvolvimento, em 1982, da tabela que é hoje uma das mais aceitas mundialmente como padrão: a denominada ETDRS⁽¹⁰⁾.

Todavia, Bailey e Lovie propuseram o uso de 5 letras como optotipos (que eram as letras usadas na tabela do padrão britânico da época), e é evidente que, para que a legibilidade dos optotipos seja similar, a melhor solução é usar o mesmo optotipo apresentado em diferentes orientações, como no caso do "C" de Landolt ou o "E", que na verdade não é a letra E, mas sim um símbolo construído por três barras pretas equidistantes intercaladas por barras brancas do mesmo tamanho e uma base preta, que se assemelha a uma letra E quando a abertura está para a direita.

Outra vantagem do uso da escala logarítmica está na possível flexibilidade quanto à distância de medida. Caso essa tenha que ser alterada, basta optar-se por uma nova distância que, dividida pela original, resulte na mesma razão entre o tamanho dos optotipos das linhas subsequentes (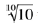 = 0,1 log, ou 1 decibel). Por exemplo, se a distância de medida original for 6 metros, usando-se a tabela à distância de 4,8 metros, deve-se adicionar 0,1 log às medidas (pegando-se a acuidade visual da linha seguinte da tabela). Caso a nova distância seja 3 metros, ou seja, a metade da distância original, o fator a ser adicionado será 0,3 log, ou três linhas (Tabela 2).

Para a construção da tabela, considerar os valores da tabela 2 referentes às dimensões dos optotipos como mostrados na figura 3 ("y") para exames em diferentes distâncias.

O valor "z" (Figura 3) corresponde à distância entre duas linhas e deve ser igual à altura dos optotipos da linha subjacente. E a distância "x" corresponde à distância entre 2 optotipos na mesma linha e deve ser igual ao tamanho deles no sentido horizontal⁽⁴⁾. Usar 5 optotipos do tipo "E" por linha em orientações aleatórias.

Uma tabela padrão está disponível no web-site do departamento de oftalmologia, otorrinolaringologia e cirurgia da Cabeça e Pescoço da Faculdade de Medicina de Ribeirão Preto -USP (http://www.fmrp.usp.br/roo/).

 

REFERÊNCIAS

1. Klein R, Klein BE, Moss SE, DeMets D. Inter-observer variation in refraction and visual acuity measurement using a standardized protocol. Ophthalmology. 1983;90(11):1357-9.         

2. Westheimer G. The spatial sense of the eye. Proctor lecture. Invest Ophthalmol Vis Sci. 1979;18(9):893-912.         

3. Schwiegerling J. Theoretical limits to visual performance. Surv Ophthalmol. 2000;45(2):139-46.         

4. Bicas HEA. Acuidade visual: medidas e notações. Arq Bras Oftalmol. 2002; 65(3):375-84.         

5. Flom MC, Weymouth FW, Kahneman D. Visual resolution and contour interaction. J Opt Soc Am. 1963;53:1026-32.         

6. Bennett AG. Ophthalmic test types. A review of previous work and discussions on some controversial questions. Br J Physiol Opt. 1965;22(4):238-71.         

7. Green J. Notes on the clinical determination of the acuteness of vision, including the construction and gradation of optotypes, and on systems of notation. Trans Am Ophthalmol Soc. 1905;10(Pt 5):644-54.         

8. Sloan LL. New test charts for the measurement of visual acuity at far and near distances. Am J Ophthalmol. 1959;48:807-13.         

9. Bailey IL, Lovie JE. New design principles for visual acuity letter charts. Am J Optom Physiol Opt. 1976;53(11):740-5.         

10. Photocoagulation for diabetic macular edema. Early Treatment Diabetic Retinopathy Study report number 1. Early Treatment Diabetic Retinopathy Study research group. Arch Ophthalmol. 1985;103(12):1796-806.         

 

 

Endereço para correspondência:
Antonio Augusto V. Cruz
Faculdade de Medicina de Ribeirão Preto da Universidade de São Paulo
Av. Bandeirantes, 3.900
Ribeirão Preto (SP) CEP 14049-900
E-mail: [email protected]

Recebido para publicação em 27.07.2009
Última versão recebida em 14.10.2009
Aprovação em 21.10.2009

 

 

Trabalho realizado no Departamento de Oftalmologia, Otorrinolaringologia e Cirurgia de Cabeça e Pescoço da Faculdade de Medicina de Ribeirão Preto da Universidade de São Paulo - USP - Ribeirão Preto (SP) - Brasil.