RESUMO

OBJETIVO: Desenvolver simulação computadorizada de ablação para produzir lentes de contato personalizadas a fim de corrigir aberrações de alta ordem. MÉTODOS: Usando dados reais de um paciente com ceratocone, mensurados em um aberrômetro ("wavefront") com sensor Hartmann-Shack, foram determinados as espessuras de lentes de contato que compensam essas aberrações assim como os números de pulsos necessários para fazer ablação as lentes especificamente para este paciente. RESULTADOS: Os mapas de correção são apresentados e os números dos pulsos foram calculados, usando feixes com a largura de 0,5 mm e profundidade de ablação de 0,3 µm. CONCLUSÕES: Os resultados simulados foram promissores, mas ainda precisam ser aprimorados para que o sistema de ablação "real" possa alcançar a precisão desejada.

Descritores: Algoritmos; Simulação por computador; Córnea; Ceratocone; Ceratectomia fotorrefrativa; Lentes de contato hidrofílicas; Modelos teóricos; Procedimentos cirúrgicos refrativos; Aumento da imagem; Interpretação de imagem assistida por computador

ABSTRACT

PURPOSE: To develop a computer simulation for customized soft contact lenses in order to correct aberrations of higher order. METHODS: Using real data from a patient diagnosed with keratoconus, which were measured using a Hartmann-Shack wavefront sensor, the thickness of the contact lenses that compensate these aberrations as well the numbers of pulses required to ablate the lenses were specifically determined for the patient. RESULTS: The maps of correction are presented and the numbers of pulses are calculated, using a 0.5 mm beam width and a 0.3 µm ablation depth. CONCLUSIONS: The results shown here are promising, but they should be improved so that the ablation in actual physical systems can reach the desired accuracy.

Keywords: Algorithms; Computer simulation; Cornea; Keratoconus; Photorefractive keratectomy; Contact lenses, hydrophilic; Models, theoretical; Refractive surgical procedures; Image enhancement; Image interpretation, computer-assisted

---

 

 

INTRODUÇÃO

O avanço dos instrumentos para diagnóstico oftálmico da acuidade visual^(1-2) proporcionou novas informações sobre distorções visuais que até então não eram possíveis. Com isso, surgiu também a necessidade de novas técnicas para corrigi-las. Atualmente é possível utilizar o sensor Hartmann-Shack para analisar aberrações ópticas de ordem mais alta do que a miopia, hipermetropia e astigmatismo e isso tem proporcionado melhorias significantes no que tange as cirurgias refrativas.

A ceratotomia radial (RK) foi uma das primeiras técnicas utilizadas para a realização de cirurgias refrativas na córnea e, a partir do uso do laser outras técnicas foram desenvolvidas, como a ceratectomia fotorrefrativa (PRK). Com o objetivo de evitar as complicações relacionadas com a cicatrização pós-PRK e reduzir o desconforto pós-operatório, criou-se a técnica chamada de laser in situ keratomileusis (LASIK)⁽³⁾. A RK, hoje em desuso, era baseada nas aplicações de incisões radiais para aplainar a córnea central, e era realizada em tratamento de baixo grau de miopia e astigmatismo. A PRK faz a correção de ametropias como miopia, hipermetropia e astigmatismo e a LASIK pode tratar hipermetropia e graus mais altos de miopia e astigmatismo⁽³⁾.

Apesar da melhoria ocorrida nessas técnicas, muitos pacientes não podem ser operados devido a doenças oculares, grau elevado, instabilidade da refração e córneas inadequadas.

Como alternativa para esses pacientes, em que até mesmo os óculos ou as lentes de contato convencionais (para correção apenas de aberrações de baixa ordem - miopia, astigmatismo e hipermetropia) não são capazes de lhes proporcionar boa acuidade visual, surge então a possibilidade da utilização de lentes de contato personalizadas⁽⁴⁾. As lentes de contato disponíveis atualmente, no mercado brasileiro, são destinadas à correção de aberrações de segunda ordem, apresentando limitações no caso de portadores de aberrações de alta ordem. Portanto, a proposta desse trabalho é desenvolver uma simulação computadorizada de ablação para produzir lentes de contato personalizadas, corrigindo aberrações de alta ordem, utilizando parâmetros de um laser como primeiro passo para construção do sistema de modelagem "real" das lentes.

A ideia de moldar lentes de contato personalizadas não é inédita, mas a técnica apresentada aqui é inovadora pelo fato de ablar lentes de contato com excimer laser. Outros grupos de pesquisas^(5-6) moldam lentes em torno de controle numérico computadorizado (CNC), que é um processo mecânico enquanto o procedimento a laser é óptico, dando assim mais liberdade e precisão para ablação de diversas formas geométricas das aberrações.

O método óptico consiste em incidir feixes do excimer laser em um espelho piezoelétrico móvel defletindo a direção de propagação dos feixes do laser e deste para a lente como se ela estivesse sendo "esculpida". Os disparos dos feixes, a posição do espelho móvel e toda a sequência de ablação estão diretamente relacionados com o mapa de correção previamente determinado por simulações matemáticas. Como se trata de um extenso assunto, com participação do nosso grupo em publicações e pesquisas anteriores^(4-7), no presente trabalho vamos abordar apenas o tema referente às simulações computadorizadas.

 

MÉTODOS

O método para analisar distorções visuais utilizando a técnica com o sensor Hartmann-Shack⁽⁷⁾ é baseado no princípio da diferença de caminho óptico (produto da distância geométrica pelo índice de refração), que equivale aos erros das frentes de onda causados por todos os componentes do olho (humor vítreo, lente ou cristalino, humor aquoso e córnea).

Matematicamente essas aberrações ópticas são representadas por uma função W(ρ ,θ ) que descreve a aberração total do olho examinado:

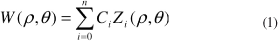
em que C_i são os coeficientes dos polinômios, Z_i(ρ ,θ ) são os polinômios de Zernike, ρ é a componente radial variando de 0 a 1 e θ é a componente azimutal variando de 0 a 2π em coordenadas polares⁽⁸⁾. Esses polinômios são os mais indicados para descrever aberrações de frentes de ondas de sistema óptico, pois são ortogonais em um círculo unitário e invariante sob rotação.

Baseando-se nesse conceito de medidas de aberrações ópticas é que consiste a ideia de moldar a lente de contato personalizada. Variando a espessura da lente, os desvios das frentes de ondas podem ser compensados de maneira personalizada. Para entender melhor esse conceito, utiliza-se o diagrama mostrado na figura 1. É possível perceber a diferença em tentar corrigir aberrações de alta ordem com uma lente de contato convencional (Figura 1A) e corrigir as mesmas aberrações usando uma lente de contato personalizada (Figura 1B). No primeiro caso apenas as aberrações de baixa ordem são corrigidas e no segundo percebe-se que as aberrações são compensadas pela superfície irregular da lente, formando uma imagem nítida na retina. Dessa maneira, a lente será mais fina onde a frente de onda tem seu maior atraso e mais espessa onde tem menor atraso ou está avançada.

 

 

O modelo matemático começa pela determinação da quantidade de material a ser retirado, ou ablado da lente e, observando o esquema da figura 1C é possível entender como isso será feito. Considerando uma lente de contato de espessura L(ρ ,θ ), uma frente de onda plana de distância P(ρ, θ ) produzida por um olho sem aberração, e uma frente de onda com aberração de distância A(ρ ,θ ) produzida por um olho não emétrope, tendo como referencial a frente de onda plana do sistema. Decompondo o caminho óptico total (da fóvea até a frente de onda com aberração), passando pelo caminho I₁, sobre o eixo óptico e o caminho I₂ marginal à córnea, tem-se:

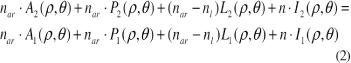
Por convenção ρ = 0 no eixo óptico do olho, isto é, no vértice da córnea. Dessa forma:

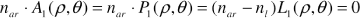
E para garantir esse esquema, a córnea, a lente e a onda com aberrações devem estar centradas no mesmo eixo. n_ar é o índice de refração do ar, n o índice de refração do meio interno do olho e n_l índice de refração da lente. Agora, substituindo essas condições na equação (2):

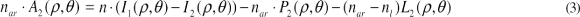
Fazendo n.(I₁(ρ ,θ ) - I₂(ρ ,θ ) ) = n . I(ρ,θ )

a equação (3) fica:

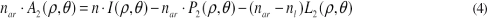
Sabendo que a diferença do caminho óptico

[n . I(ρ,θ ) - n_ar . P₂(ρ ,θ )] é a medida realizada pelo aberrômetro, ou seja, os coeficientes de Zernike representado pela função W(ρ ,θ ), ver equação (1), então a equação (4) reduz a:

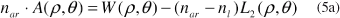
e considerando que a espessura da lente seja suficiente para a correção da aberração final, A(ρ ,θ ) tem que ser zero, portanto:

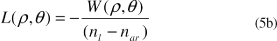
Essa equação permite determinar as espessuras das lentes de contato personalizadas conhecendo a função W(ρ ,θ ) de qualquer olho examinado.

O próximo passo é determinar o número de pulsos do laser necessários para retirar material da lente, ou melhor, ablar a lente.

O número de pulsos por região é definido pela razão entre a espessura da lente (ver equação (5b)) e a profundidade de ablação de um pulso do laser (D):

Nesta etapa da simulação foram considerados apenas parâmetros como largura do feixe e profundidade de ablação do laser, com valores adotados da literatura⁽⁹⁾. A ferramenta de programação utilizada para calcular os dados foi o MATLAB (MATrix LABoratory) da empresa Mathworks⁽¹⁰⁾ por ser tratar de um software interativo de alta performance voltado para o cálculo numérico. Os resultados gerados a partir das equações demonstradas acima serão apresentados a seguir.

Para testar a técnica simulada aqui apresentada, foram utilizadas medidas realizadas em paciente com ceratocone (aberrações de ordem alta).

A partir dos dados apresentados, no mapa de aberração, e com os índices de refração do ar (n_ar = 1,00) e da lente (n_l = 1,43), adotado da literatura⁽¹¹⁾, foi utilizada a equação (5b) para determinar as espessuras da lente para esse paciente.

Nesse artigo será mostrado o resultado inicial da primeira etapa do projeto de Lentes de Contato Personalizadas, ou LCP, usando algoritmos desenvolvidos na Escola Paulista de Medicina (UNIFESP) em parceria com o laboratório de Óptica Oftálmica do IFSC - USP para um olho com ceratocone.

 

RESULTADOS

O mapa de aberrações das frentes de onda do paciente é mostrado na figura 2A e pelo código de cor ao lado pode-se perceber o quão agudo é esse caso de ceratocone, com valores que chegam a mais de 20 µm. A figura 2B mostra o perfil desses dados.

O mapa de correção é mostrado na figura 2C. Pode-se ver pelas figuras 2A e 2C que elas são como espelhos uma da outra, ou seja, como o mapa de ablação tem como objetivo deixar o mapa de aberrações como uma frente de onda plana, um é o "oposto" do outro em termos de visualização. Dessa forma, nota-se que na região em que as cores são quentes na figura 2A, na mesma região na figura 2C elas são frias.

O mapa de correção das figuras 2E e 2F foram gerados acrescentando uma constante aos dados dos mapas das figuras 2C e 2D para satisfazer a condição de que um pulso não pode ter valores negativos ou que na lente não se pode adicionar material, somente retirar. É importante observar que isso não afeta a forma básica do mapa de correção. Com as figuras 2D e 2F fica mais fácil visualizar os valores das espessuras das lentes a serem abladas.

O material escolhido para moldar a lente será o polimetil metacrilato (PMMA), pois há estudos^(12-15) que demonstram a viabilidade de ablação com laser nesse tipo de material. Nestes estudos, foi avaliada a interação entre o excimer laser (ArF, Argon Fluoride com λ = 193 nm) e o PMMA e mostrou-se que é possível ablá-los com pouco aquecimento e pouca deposição de material. Entretanto para a simulação, apenas o índice de refração (característica óptica do material) é necessário como parâmetro de entrada nos cálculos.

Com os valores das espessuras determinadas, foi calculada a quantidade de pulsos necessários para modelar a lente utilizando a equação (6). Parâmetros como largura do feixe do laser de 0,5 mm e profundidade de ablação de 0,3 µm, também foram adotadas da literatura⁽⁹⁾.

Os mapas de distribuição dos pulsos calculados são mostrados na figura 3. A diferença entre as figuras 3A e 3B é que a primeira foi gerada com os dados do mapa de correção da figura 2C e a segunda com o mapa de correção da figura 2E, ou seja, escalonando os valores negativos dos pulsos para valores positivos.

 

DISCUSSÃO

Os resultados apresentados mostraram que o algoritmo para modelar lentes de contato personalizadas para compensar aberrações de ordem alta pode ser eficaz. Entretanto, para a construção do sistema experimental será preciso um algoritmo muito mais refinado com características, por exemplo, do perfil real do laser e sobreposição dos feixes, ou seja, dados e fenômenos que ocorrem na prática.

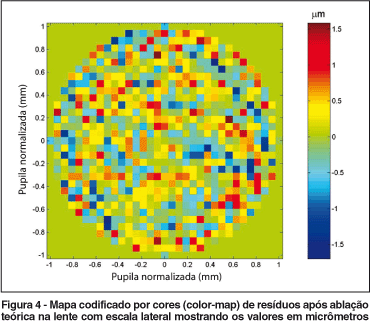
Nessa etapa do algoritmo, foram utilizados apenas parâmetros como tamanho do "spot" e profundidade de ablação do laser. Os excimers lasers oferecidos no mercado têm dois tipos de perfis, um "top hat" (ou quadrado) que tem intensidade constante dentro de um diâmetro fixado, caindo a zero em qualquer lugar fora dele e outro gaussiano, em que a intensidade decresce exponencialmente⁽¹⁶⁾. Um excelente parâmetro para avaliar-se a qualidade da ablação teórica realizada nesse trabalho é o mapa residual mostrado na figura 4. Observou-se que o resíduo da simulação computadorizada tem uma precisão baixa pelo fato de ter sido adotado o feixe com perfil quadrado e não ter sido considerada a sobreposição dos feixes (ou seja, o passo do espelho móvel). Observando a figura e acompanhando o código de cor ao lado percebe-se que em alguns pontos (quadrinhos verdes), a ablação foi total enquanto que em outros permaneceram alguma aberração.

 

 

Mas pelo fato de a quantidade de pulsos liberados pelo laser ser uma variável discreta, sempre haverá algum resíduo pós-ablação, até mesmo utilizando algoritmos mais refinados. Ou seja, só é possível retirar quantidade de material que seja múltipla da profundidade da ablação do laser. Assim, as mudanças promovidas pela ablação estão limitadas pelos parâmetros disponíveis dos lasers comerciais. Por isso a importância em considerar perfil gaussiano, sobreposição dos feixes para minimizar esses resíduos e dessa forma, serem obtidas superfícies com perfis mais suaves como se a lente tivesse sido de fato esculpida. Portanto, o próximo passo é melhorar o algoritmo, inserindo dados mais reais na simulação.

 

CONCLUSÕES

No presente estudo foi possível determinar o perfil e o número de pulsos necessários para produzir uma lente de contato personalizada utilizando-se uma simulação com excimer laser para dados obtidos em um wavefront usando o sensor Hartmann-Shack. O algoritmo desenvolvido mostrou que, caso não seja considerado fatores como sobreposição, o formato circular e o perfil de intensidade gaussiano do laser, os resíduos obtidos pós-ablação são inaceitáveis, do ponto de vista da correção refrativa. Esta pesquisa mostrou ainda a importância de serem considerados todos os recursos e características do laser, para que, na fase prática do instrumento de ablação de lentes, resultados mais próximos possíveis daqueles da fase de simulação sejam obtidos.

 

REFERÊNCIAS

1. Carvalho LA, Castro JC, Chamon W, Schor P. A new wavefront sensor with polar symmetry: quantitative comparisons with a Shack-Hartmann wavefront sensor. J Refract Surg. 2006;22(9):954-8.         

2. Carvalho LA, Castro JC, Carvalho LA. Measuring higher order optical aberrations of the human eye: techniques and applications. Braz J Med Biol Res. 2002; 35(11):1395-406.         

3. Sakimoto T, Rosenblat MI, Azar DT. Laser eye surgery for refractive errors. Lancet. 2000;367(9520):1432-47.         

4. Sabesan R, Jeong TM, Carvalho LA, Cox IG, Williams DR, Yoon G. Vision improvement by correcting higher order aberrations with customized soft contact lenses in keratoconic eyes. Opt Lett. 2007;32(8):1000-2.         

5. Customized Vision Correction Laboratory [home page on Internet]. Rochester, NY: University of Rochester; 2008. [Cited 2008 Jul 5]. Available from: http://www.cvs.rochester.edu/yoonlab        

6. Carvalho LA, Yoon G. Medindo o poder refrativo de lentes de contato gelatinosas personalizadas. Arq Bras Oftalmol. 2007;70(1):67-72.         

7. Carvalho LA, Castro JC. Preliminary results of instrument for measuring the optical aberrations of the human eye. Braz J Phys. 2003,33(1):140-7.         

8. Thibos LN, Applegate RA, Schwiegerling JT, Webb R; VSIA Standards Taskforce Member Vision Science and its applications. Standards for reporting the optical aberrations of eyes. J Refract Surg. 2002;18(5):S652-60.         

9. Huang D, Arif M. Spot size and quality of scanning laser correction of higher-order wavefront aberrations, J Cataract Refract Surg. 2002;28(3):407-16.         

10. MATLAB- The Mathworks accelerating the pace of engineering and science [home page on Internet]. The Language of technical computing. Natick, MA; Mathworks; 2008. [Cited 2008 Sept 15]. Available from: http://www.mathworks.com/products/matlab/        

11. Lewis JR, Knellinger AE, Mahmoud AM, Mauger TF. Effect of soft contact lenses on optical measurements of axial length and keratometry for biometry in eyes with corneal irregularities Invest Ophthalmol Vis Sci. 2008;49(8):3371-8.         

12. Nicolson PC, Vogt J. Soft contact lens polymers: an evolution. Biomaterials. 2001;22(2):3273-83.         

13. Fuxbruner A, Hemo I, Lewis A, Zauberman H, Blau D, Polotsky D. Controlled lens formation with unapertured excimer lasers: use with organic polymers and cornel tissues. Applied Optics. 1990;29(36):        

14. Dorronsoro C, Cano D, Merayo-Lloves J, Marcos S., Experiments on PMMA models to predict the impact of corneal refractive surgery on corneal shape. Optical Soc Am. 2006;14(13):6142-56.         

15. Kitai MS, Popkov LV, Semchishen VA, Kharizov A. The Physics of UV Laser cornea ablation. IEEE J Quantum Electronics. 1991;27(2):302-7.         

16. Carvalho LA. Simulação computacional de cirurgias foto-refrativas personalizadas e precisão relacionada à ordem das aberrações ópticas. Arq Bras Oftalmol. 2007;70(6):917-23.         

 

 

Endereço para correspondência:
Grupo de Óptica
Instituto de Física de São Carlos Universidade de São Paulo
Av. Trabalhador Sãocarlense, 400 - Caixa Postal 369
São Carlos (SP)
CEP 13560-970
E-mails: [email protected], [email protected]

Recebido para publicação em 22.09.2008
Última versão recebida em 18.01.2009
Aprovação em 26.01.2009

 

 

Trabalho realizado no Grupo de Óptica do IFSC-USP em parceria com a Escola Paulista de Medicina, Universidade Federal de São Paulo - UNIFESP - São Paulo (SP).
Nota Editorial: Depois de concluída a análise do artigo sob sigilo editorial e com a anuência do Dr. Paulo Ricardo de Oliveira sobre a divulgação de seu nome como revisor, agradecemos sua participação neste processo.