RESUMO

O objetivo principal deste trabalho foi o desenvolvimento e a implementação de um algoritmo para simulação de cirurgias foto-refrativas. Sabe-se que os atuais " flying-spot" lasers para cirurgia refrativa disponíveis no mercado ainda contêm limitações na correção de algumas aberrações de ordem alta. No entanto, há muito pouca informação quantitativa sobre os erros envolvidos em função da complexidade das aberrações. Aplicando-se superfícies objetivo descritas por uma série de coeficientes de Zernike e o conceito matemático de convolução, várias ablações personalizadas foram simuladas para várias aberrações, desde baixa ordem (esfero-cilíndricas) até aberrações de décima ordem (como coma, aberração esférica, entre outras). Os resultados mostram que o perfil de ablação de cada pulso do laser assim como seu diâmetro são fatores críticos quando o objetivo é corrigir aberrações de alta ordem. Além disso, outras conclusões foram possíveis, como por exemplo a de que nem todas as aberrações de alta ordem induzem aos mesmos erros na ablação. Também foi possível verificar que a correção de aberrações de alta ordem nos termos radiais (como aberração esférica) é bem mais difícil do que naqueles termos contendo alta frequência angular (como trefoil).

Descritores: Erros de refração; Simulação por computador; Refração ocular; Calibragem; Algoritmos; Cirurgia assistida por computador

ABSTRACT

PURPOSE: To develop and implement an algorithm for simulation of photorefractive surgery. It is well known that many flying-spot lasers in the market have limitations in correcting higher order aberrations, but there is little quantitative information about errors related to aberration complexity. METHODS: By applying known surfaces described by Zernike polynomials of different orders it was possible to simulate several target surfaces that may well resemble in vivo cases of refractive surgery candidates. An algorithm that uses the mathematical concept of convolution was implemented and several simulated surfaces were tested, ranging from low order aberrations (sphere-cylinder) to 10th order aberrations, (high orders of coma, spherical aberration, trefoil, etc). RESULTS: the results show that the laser profile and diameter are critical factors when considering the correction of higher order aberrations. CONCLUSIONS: Not all aberrations of the same high order induce the same amount of error - spherical aberrations are shown to be far more difficult to correct than higher order aberrations related to angular frequency.

Keywords: Refractive errors; Computer simulation; Refraction, ocular; Calibration; Algorithms; Surgery, computer-assisted

---

 

 

INTRODUÇÃO

Há vários anos as cirurgias refrativas a laser praticamente substituiram as cirurgias realizadas com bisturi (ceratotomia radial)^(1-2). Esta última entrou gradualmente em desuso pelas suas próprias limitações. A realização de cortes radiais na córnea permitiam apenas a correção de algumas ametropias (principalmente miopia), dentro de um " range" limitado de poder dióptrico e não permitia a correção de aberrações ópticas de ordem mais alta do que desfocalização (miopia ou hipermetropia) e astigmatismo. Por outro lado, as ablações realizadas com laser excimer, desde as primeiras versões destas máquinas, permitiam correções mais precisas e previsíveis^(3-4). Com a evolução dos algoritmos, da potência, do perfil de intenside e do tamanho, flexibilidade de movimento e rapidez do spot (daí o termo " flying-spot" ), os lasers excimers foram sendo aprimorados até conseguir-se moldar a superfície da córnea com maior precisão e de maneira personalizada. Esta evolução foi importante e significa que nos dias de hoje há a possibilidade real de correções não somente das aberrações de baixa ordem (esfero-cilíndricas ou segunda ordem) como aquelas de alta ordem (coma, aberração esférica, entre outras, ou seja, acima de ordem 2). No entanto, ainda não se conhece bem as limitações destes lasers para estas aberrações de ordem alta - é preciso salientar que qualquer termo de ordem mais alta que 2 é classificado como sendo de " alta ordem" , mas não há hoje limites claros de até qual ordem é possível corrigir com precisão aceitável. Obviamente que, por se tratar de uma simulação apenas do aspecto da ablação em sí, não estamos considerando fatores que tornam a cirurgia personalizada um assunto ainda mais complexo, como, por exemplo, as reações biomecânicas da córnea^(5-6).

Embora a cirurgia refrativa a laser esteja cada vez mais difundida entre médicos e pacientes nos dias de hoje, e também embora sua precisão tenha evoluído bastante nos últimos anos com o advento de lasers " flying spot" ⁽⁷⁾, ainda há bastante espaço para aprimoramento dos algoritmos⁽⁸⁾ para que a nova geração de cirurgias refrativas, as chamadas cirurgias refrativas personalizadas, seja alcançada com sucesso. Como veremos na seção sequinte, o tamanho do spot do laser, o conhecimento da região em torno da ablação maior do que a própria região a ser ablada, o perfil (gaussiano ou " flat hat" ) e eficiência do laser, são todas informações importantes a serem consideradas para otimização dos atuais algoritmos.

Dentro deste processo todo de pesquisas para se chegar a lasers e algoritmos mais precisos, nosso grupo participou ativamente^(9-10) do projeto de confecção de lentes de contato personalizadas (LCP) na University of Rochester⁽¹¹⁾ no qual um dos objetivos era usar lasers excimer também para moldar superfícies de lentes de contato. Desta experiência surgiu o interesse de nosso grupo de pesquisa em implementar um sistema que possa realizar a ablação personalizada destas lentes usando laser excimer ao contrário de tornos computadorizados, aumentando a precisão do processo. Acreditmaos que, ao mesmo tempo que estas pesquisas possam ter retorno promissor para as LCP, também possa gerar conhecimento e excelência para que, futuramente, estes algoritmos sejam utilizadas para construção do primeiro laser genuinamente brasileiro para ablações de córneas in vivo. O trabalho de construção de um algoritmo de ablação e a simulação computacional demonstrado aqui é o primeiro passo para um futuro sistema como estes.

 

MÉTODOS

Software

Inicialmente, foi implementado uma série de cálculos para o modelamento matemático do processo de ablação. Baseado nestes cálculos foi implementado então um algoritmo que realiza a simulação computacional do processo de ablação. Este primeiro passo é importante para ter-se certeza de que o algoritmo está funcionando corretamente antes que ele seja testado na prática. Para esta etapa foi necessária a escolha de uma ferramenta de programação ao mesmo tempo robusto e flexível para que se possa testar de maneira eficiente vários algoritmos. Em trabalhos anteriores que envolviam processamento de imagens e algoritmos para topografia de córnea tivemos sucesso com a ferramenta Matlab da empresa Mathworks⁽¹²⁾. Portanto neste trabalho atual utilizamos também esta ferramenta.

Teoria da ablação

A córnea ou a LC podem ter suas superfícies ou suas aberrações ópticas descritas usando um sistema de coordenadas cilíndricas como aquele mostrado na figura 1.

 

 

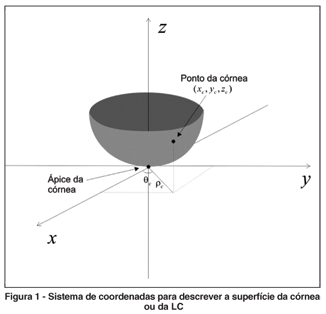
Através de medidas realizadas no topógrafo de córnea^(13-17) ou no sensor de frentes de onda (Hartmann-Shack) pode-se obter medidas da superfície/aberrações da córnea ou da lente de contacto -LC com precisões de 0,2 micrômetros, representados por h(r,q). Estes valores de medidas são então interpolados por um conjunto de coeficientes de Zernike, de tal maneira que podem ser representados pela somatória:

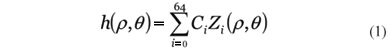
Onde C representa os valores normalizados de cada coeficiente que multiplica um dos polinômios de Zernike Z. Aqui, por motivos de didática, estamos utilizando o sistema de indexação de um único índice (i), mas é importante salientar que a convenção da Optical Society of America recomenda a utilização de um índice separado para freqüência radial (n) e outro para angular (m), aos quais estaremos nos referindo na parte de resultados. Para maiores informações sobre a teoria dos coeficientes de Zernike consulte⁽¹⁸⁾.

Chamaremos aqui a função objetivo de T, que teoricamente é simplesmente a subtração da superfícies pós-ablação (POS) da pré-ablação (PRE):

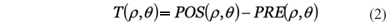
A função objetivo T (r,q) é fácil de ser calculada desde que saibamos quais as aberrações que se deseja corrigir⁽¹⁹⁾. Depois de medida a função PRE (r,q) e computada a função pós-cirurgia refrativa POS (r,q), tanto para a córnea como para uma lente de contato, a função objetivo T (r,q) passa a ser conhecida com precisão. Depois de computada a função objetivo esta é inserida no algoritmo que aproxima esta superfície por polinômios de Zernike. Este é um processo importante já que um dos principais testes do algoritmo é verificar a capacidade de correção das aberrações em função da ordem dos polinômios de Zernike. Normalmente quão maior a ordem destes coeficientes mais complexa a superfície⁽²⁰⁾. Para uma classificação detalhada dos Polinômios de Zernike e suas propriedades matemáticas favor consultar a referência 18.

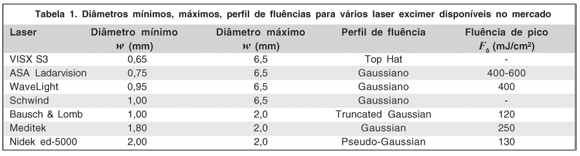
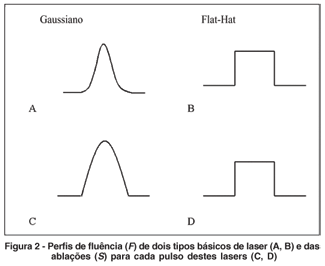
O próximo passo é modelar matematicamente o perfil de ablação de cada pulso do laser. Há vários tipos de perfis de distribuição de intensidade (fluência) do laser. Na tabela 1 listamos alguns dos modelos de diferentes fabricantes e seus principais parâmetros. Basicamente há dois tipos de perfil: o gaussiano e o " top hat" , que podem ser vistos na figura 2 (A, B).

 

 

 

 

As equações que descrevem estes dois perfis de fluência são:

Gaussiana

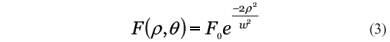
Onde w é o diâmetro do feixe e F₀ é o pico da fluência.

Flat-Hat

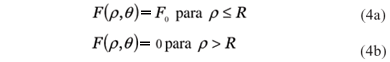
Onde R=w/2.

Apesar da fluência do laser poder ser definida pela função Gaussiana ou top-hat (Figura 2 (A, B)), não é este o perfil de ablação impresso na córnea ou na LC, conforme pode ser visto pela figura 2 (C, D). Estudos usando microscopia eletrônica⁽²¹⁾ mostram que o perfil de ablação pode ser modelado a partir do perfil de intensidades pela seguinte expressão:

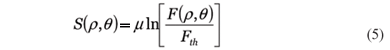
Onde µ é a eficiência do laser, dada em micrômetros, a função F descreve a fluência do laser, ou seja, é uma medida de quanto ele retira de tecido/material em função da posição para um único pulso, conforme descrito pelas equações (3) e (4); F_th é a fluência de limiar, ou seja, a mínima fluência que ainda retira ou abla o tecido ou o material (no caso da córnea e de um material acrílico ou plástico estes valores são diferentes e devem ser corretamente alimentados no programa). Na figura 2 (C, D) podemos ver o perfil da função S para ambas as diferentes fluências mostradas na parte superior da mesma figura. Estes dois perfis podem ser utilizados em nossas simulações. No entanto, quando formos testar o algoritmo em termos práticos, faz-se necessário modelar o pulse de acordo com as especificações do fabricante, ou seja, se a função fluência é uma gaussiana ou um " flat hat" . Estas especificações, conforme pode ser visto na tabela 1, são fornecidos pelo fabricante.

O modelamento matemático da ablação da superfície objetivo T pelo perfil de ablação do laser S será realizado utilizando-se o conceito matemático de convolução⁽²²⁾. Sendo assim a superfície pós-ablação pode ser descrita como:

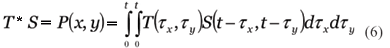
Onde t é o valor máximo assumido no domínio tanto para a direção x quanto para y, dt_x e dt_y são as elementos infinitesimais de variação em x e y conforme a função T é convoluída com a função S. A mudança de coordenadas de cartesiana para polar é dada pelas simples equações:

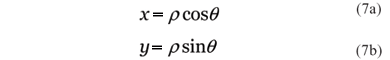
Apesar de P conter o formato correto do resultado pós-ablação, não está escalonado corretamente. A função P deve ser escalonada, depois da convolução utilizando-se a equação:

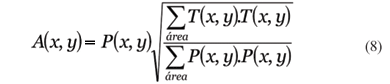
Após o escalonamento, a função A (r,q) descreve a superfície pós-ablação teórica, ou seja, supondo-se que o laser tem deslocamento infenitesimal sobre a superfície e que o número de feixes é virtualmente infinito, esta função descreve a superfície ideal após a retirada de tecido/material. Como nenhuma destas condições é verdadeira na prática, temos que calcular o real número de pulsos que devem ser disparados para cada região da superfície. Para isso temos que levar em conta a capacidade real de deslocamento do feixe, a eficiência µ e a largura do feixe. Para mensurar a diferença entre superfície objetivo (desejada) e a superfície obtida, computamos o erro quadrático médio (EQM) entre a superfície desejada (T) e aquela obtida pela ablação simulada (A) usando a expressão:

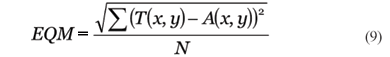
Onde N é o número total de pontos considerados e a somatória é realizada para todos os valores dentro da área de ablação.

 

RESULTADOS

Como mostrado na tabela 1 há vários fabricantes de laser e vários parâmetros do laser. Neste trabalho realizamos a simulação de lasers com perfil gaussiano e top-hat e utilizando parâmetros como largura do feixe (w) de 500 a 2.000 micrômetros, em passos de 50 micrômetros, de tal maneira a cobrir a maioria dos diâmetros disponíveis para lasers comerciais. Para a fluência de pico P₀ utilizamos um valor médio de 290 mJ/cm². Para a eficiência µ e para fluência de limiar F_th foram utilizados valores disponíveis na literatura⁽⁸⁾, 0,3 mµ e 60 mJ, respectivamente.

Todos estes diferentes parâmetros foram testados em diferentes superfícies objetivo, de acordo com a complexidade da superfície, ou seja, de acordo com a ordem das aberrações. Para isso geramos várias superfícies objetivo T variando os coeficientes de Zernike desde esfero-cilíndrico até aberrações de décima ordem. As primeiras 66 superfícies de Zernike podem ser vistas na figura 3. Como cada olho humano é singular no que tange aos tipos de aberrações, acreditamos que esta seja a maneira mais objetiva de testar nosso algoritmo, pois a maioria das aberrações desde olhos normais até olhos com ceratocone ou pós-ceratoplastia, podem ser representados por polinômios de Zernike até a décima ordem⁽²⁰⁾.

 

 

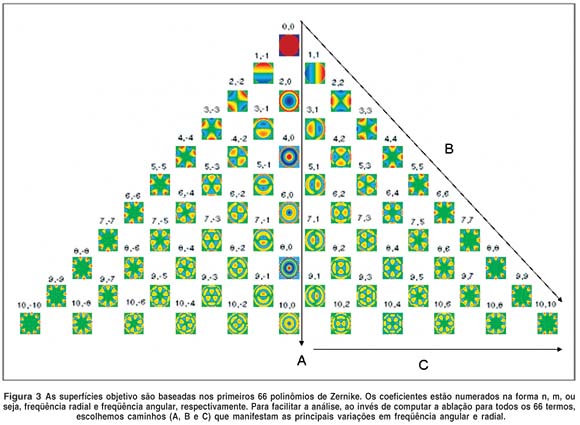
Como podemos ver pela figura 3 há 66 superfícies de Zernike para caracterizar variações da ordem tanto radial como angular até a décima ordem. Como vimos acima, o termo radial n varia de 0 a 10 (de cima para baixo na pirâmide) e o termo angular varia de -10 a 10 (da esquerda para direita na pirâmide). Não há necessidade, para averiguar a precisão do algoritmo, em simular todas estas 66 aberrações; apenas utilizando os caminhos A, B e C é possível avaliar o desempenho do algoritmo de forma mais compacta e levando em conta as características essencias das aberrações. No caminho A temos uma variação cresente de frequêcia radial, sem variação de freqüência angular, ou seja, são termos que contém apenas variação das aberrações esféricas e são rotacionalmente simétricos. Desta maneira fica ao mesmo tempo didático e eficiente o processo de análise quantitativa da precisão do algoritmo em função dos parâmetros do laser e das características da superfície. No caminho B temos variação cresente de freqüência angular e radial e no caminho B temos apenas variação de freqüência angular, mantendo a freqüência radial constante.

Com relação ao laser, como as nossas variáveis básicas são o tipo de perfil de fluência do laser (Top-Hat ou Gaussiano), o tamanho do spot (de 50 a 2.000 micrômetros), resolvemos então plotar 2 conjuntos de 3 gráficos diferentes: o primeiro conjunto (1) usa feixe gaussiano e o outro (2) usa feixe top-hat, mostrando o erro quadrátido médio para cada diâmetro do feixe em função da ordem da aberração para cada um dos caminhos (A, B e C). Estes gráficos podem ser vistos na figura 4.

 

 

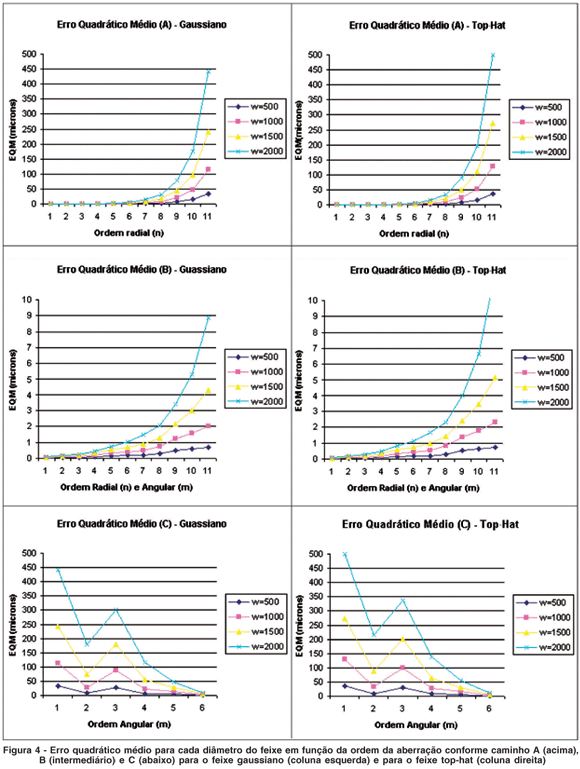
Estes gráficos mostram várias características interessantes do algoritmo de ablação, as quais analisamos na seção seguinte.

 

DISCUSSÃO

Diferenças entre feixe Gaussiano e Top-Hat

De maneira geral a comparação para cada caminho indica que o feixe gaussiano é mais preciso que o top-hat para todos os caminhos (A, B e C). Este aspecto já era esperado pois o feixe gaussiano permite " moldar" a superfície com maior precisão na interface entre pulsos de laser vizinhos, algo que já não é possível com o top-hat. Isto se deve ao próprio formato do perfil de ablação para cada feixe, sendo que no Gaussiano há uma decréscimo exponencial do perfil e no top-hat este decréscimo não existe. Por este motivo podemos concluir que, independentemente dos diâmetros de feixe disponíveis no laser comercial, o laser ideal seria aquele que tem feixes gaussianos ao invés de top-hat. Além disso, fica óbvio pelos gráficos que quão menor o diâmetro do feixe mais precisa a ablação, qualquer que seja a aberração. Isto também indica que, no caso específico de laser para cirurgia personalizada, o ideal seria o laser que tem o menor feixe de laser e que tenha perfil gaussiano. Infelizmente fenômenos ópticos como intereferência tornam a construção de lasers de feixe menores que 500 micrômetros extremamente complexa em termos ópticos, o quê obviamente tem consequências no custo final de sistemas que tenham feixes pequenos.

Diferenças para cada tipo de variação de aberrações (caminhos A, B e C)

Olhando para apenas a variação devido à complexidade das aberrações é interessante observar que, tanto para o feixe gaussiano como para o top-hat, as aberrações esféricas (caminho A) são as mais difíceis de se corrigir (Figura 4 (superior)). Pode-se observar no caminho A um aumento exponencial da imprecisão do laser com o aumento da frequência radial, chegando a valores de 450 micrômetros para o feixe Gaussiano e 500 micrômetros para o top-hat, para feixes de 2.000 micrômetros em diâmetro. A conclusão é óbvia: para feixes de 2.000 micrômetros em diâmetro e aberrrações esféricas de alta ordem a imprecisão é inadmissível, chegando a vaores próximos à própria espessura de uma córnea humana. E mesmo para feixes de 500 micrômetros em diâmetro, os erros chegam próximo a 50 micrômetros para aberrações de alta ordem; isso nos faz concluir que, para correção eficiente em pacientes com alta ordem de aberração esférica, faz-se necessário feixes com diâmetros menores que 500 micrômetros, algo que muitos fabricantes devem estar em processo de desenvolvimento.

Com relação à variações angulares e radiais de freqüência (caminho B) observamos um fenômeno interessante: não importa que a freqüência radial seja grande (até ordem 10) mas se a freqüência angular também for grande, as precisões nas ablações são maiores do que quando temos somente freqüência radial alta. Isto pode ser observado com ainda mais clareza no caminho C, onde não há variação da freqüência radial. Este fenômeno, em primeira instância, pode até causar surpresa pois era de se esperar o contrário; no entando, podemos observar pela figura 3, tanto no caminho B como C, que conforme as freqüências angular e radial aumentam, a região central dos mapas fica mais uniforme e as bordas passam a ficar bastante distorcida - pois é justamente este fenômeno que faz com que os erros sejam menores do que para o caminho A.

 

CONCLUSÃO

Desta maneira podemos concluir algo que parece até mes mo surpreendente: é mais fácil corrigir aberrações de um olho que tenha um conjunto de altas ordens de aberração esférica e astigmatismos irregulares do que se este paciente tivesse apenas aberração esférica de alta ordem! Parece incoerente, mas os gráficos demonstram que o laser teria maior precisão na zona óptica de casos que contenham também astigmatismo.

 

REFERÊNCIAS

1. Cherry PM, Britton R. Experimental radial keratectomy in rabbits for the correction of aphakia. Cornea. 1984;3(1):61-4.         

2. Teranishi C. [Study on the effects of different keratectomies for astigmatism in rabbits' eyes]. Hokkaido Igaku Zasshi. 1988;63(1):56-71. Japanese.         

3. Kriegerowski M, Bende T, Seiler T, Wollensak J. [The ablation behavior of various corneal layers]. Fortschr Ophthalmol. 1990;87(1):11-3. German.         

4. McDonald MB, Frantz JM, Klyce SD, Salmeron B, Beuerman RW, Munnerlyn CR, et al. One-year refractive results of central photorefractive keratectomy for myopia in the nonhuman primate cornea, Arch Ophthalmol. 1990;108(1): 40-7.         

5. Roberts C. Biomechanical customization: the next generation of laser refractive surgery. J Cataract Refract Surg. 2005;31(1):2-5.         

6. Carvalho L, Prado M, Cunha R, Costa A, Schor P, Chamon W. Finite element corneal model with regional young modulus predicts keratoconus. Invest Ophthalmol Vis Sci. 2006;47: E-Abstract 1334.         

7. Stojanovic A, Nitter TA. 200 Hz flying-spot technology of the LaserSight LSX excimer laser in the treatment of myopic astigmatism: six and 12 month outcomes of laser in situ keratomileusis and photorefractive keratectomy, J Cataract Refract Surg. 2001;27(8):1263-77.         

8. Huang D, Arif M. Spot size and quality of scanning laser correction of higher-order wavefront aberrations, J Cataract Refract Surg. 2002;28(3):407-16.         

9. Sabesan R, Carvalho LA, Jeong TM, Yoon G, Somasundaram R, Cox I. Correcting higher order aberrations using customized soft contact lenses in keratoconic eyes. Invest Ophthalmol Vis Sci. 2006;47:E-abstract 1205.         

10. Sabesan R, Jeong TM, Carvalho L, Cox IG, Williams DR, Yoon G. Vision improvement by correcting higher order aberrations with customized soft contact lenses in keratoconic eyes. Optics Letters [serial on the Internet]. 2007         

11. Customized Vision Correction Laboratory . Rochester, NY: University of Rochester; 2007. . Available from: http://www.cvs.rochester.edu/yoonlab        

12. The Mathworks accelerating the pace of engineering and science. MATLAB- The Language of technical computing. Natick, MA; Mathworks; 2007. . Available from: http://www.mathworks.com/products/matlab/?BB=1        

13. Carvalho LA, Stefani M, Romao AC, Carvalho L, de Castro JC, Tonissi S, et al. Videokeratoscopes for dioptric power measurement during surgery. J Cataract Refract Surg. 2002;28(11):2006-16.         

14. Carvalho LA, Schor P, Chamon W, Castro JC. Instrumento computadorizado para medidas in vivo do poder refrativo da córnea durante o ato cirúrgico. Rev Fís Apl Instrument. 2004;17(1):1-6.         

15. Carvalho L, Tonissi SA, Castro JC. Preliminary tests and construction of a computerized quantitative surgical keratometer, J Cataract Refract Surg. 1999; 25(6):821-6. Comment in: J Cataract Refract Surg. 2000;26(8):11045.         

16. Carvalho LA, Tonissi SA, Castro JC. Preliminary results of a computerized Placido disc surgical corneal topographer. In: 9º SPIE conference on Ophthalmic Technologies San Jose, California: January 1999. v.3591, p.53-62.         

17. Carvalho LA, Tonissi SA, Romão AC, Santos LE, Yasuoka F, Oliveira AC, et al. Desenvolvimento de um instrumento computadorizado para medida do poder refrativo da córnea (videoceratógrafo). Arq Bras Oftalmol. 1998;61(6) 640-54.         

18. Born M, Wolf E. Principles of optics: electromagnetic theory of propagation, interference and diffraction of light. 7ª ed. Cambridge: Cambridge University Press; 1999.         

19. Klein S. Optimal corneal ablation for eyes with arbitrary Hartmann-Shack aberrations. J Opt Soc Am A. 1998;15(9):2580-8.         

20. Carvalho LA. Accuracy of Zernike polynomials to characterize optical aberrations and the corneal surface of the eye. Invest Ophthalmol Vis Sci. 2005; 46(6):1915026.        

21. Mrochen M, Semshichen V, Funk RH, Seiler T. Limitations of erbium:YAG laser photorefractive keratectomy. J Refract Surg. 2000;16(1):51-9.         

22. Butkov E. Mathematical Physics. Facsimile ed. Massachusets: Addison Wesley; 1968. (Series in advanced physics).        

 

 

Endereço para correspondência:
Av. Trabalhador São Carlense, 400 - Caixa Postal 369
São Carlos (SP) CEP 13560-970
E-mail: [email protected]

Recebido para publicação em 08.10.2006
Última versão recebida em 02.05.2007
Aprovação em 09.08.2007

 

 

Trabalho realizado no Grupo de Óptica, Laborat