RESUMO

OBJETIVO: Embora tenha sido proposto que a vasculatura retínica apresenta estrutura fractal, nenhuma padronização do método de segmentação ou do método de cálculo das dimensões fractais foi realizada. Este estudo objetivou determinar se a estimação das dimensões fractais da vasculatura retínica é dependente dos métodos de segmentação vascular e dos métodos de cálculo de dimensão. MÉTODOS: Dez imagens retinográficas foram segmentadas para extrair suas árvores vasculares por quatro métodos computacionais ("multithreshold", "scale-space", "pixel classification" e "ridge based detection"). Suas dimensões fractais de "informação", de "massa-raio" e "por contagem de caixas" foram então calculadas e comparadas com as dimensões das mesmas árvores vasculares, quando obtidas pela segmentação manual (padrão áureo). RESULTADOS: As médias das dimensões fractais variaram através dos grupos de diferentes métodos de segmentação, de 1,39 a 1,47 para a dimensão por contagem de caixas, de 1,47 a 1,52 para a dimensão de informação e de 1,48 a 1,57 para a dimensão de massa-raio. A utilização de diferentes métodos computacionais de segmentação vascular, bem como de diferentes métodos de cálculo de dimensão, introduziu diferença estatisticamente significativa nos valores das dimensões fractais das árvores vasculares. CONCLUSÃO: A estimação das dimensões fractais da vasculatura retínica foi dependente tanto dos métodos de segmentação vascular, quanto dos métodos de cálculo de dimensão utilizados.

Descritores: Fractais; Retina; Técnicas de diagnósticos e procedimentos; Biometria

ABSTRACT

PURPOSE: Although it has been proposed that retinal vasculature is fractal, no method of standardization has been performed for vascular segmentation or for dimension calculation, thus resulting in great variability among values of fractal dimensions. The present study was designed to determine if estimation of retinal vessel fractal dimensions is dependent on vascular segmentation and dimensional calculation methods. METHODS: Ten eye fundus images were segmented to extract their vascular trees by four computational methods ("multithreshold", "scale-space", "pixel classification" and "ridge based detection"). Their information, mass-radius and box counting fractal dimensions were calculated and compared with those of the same vascular trees manually segmented (gold standard). RESULTS: The mean vascular tree dimension varied among the groups of different segmentation methods, from 1.39 to 1.47 for box counting, from 1.47 to 1.52 for information and from 1.48 to 1.57 for mass-radius dimensions. The utilization of different vascular segmentation methods and different dimension calculation methods introduced significant difference among fractal dimension of vessels. CONCLUSION: Estimation of retinal vessel fractal dimensions was dependent on both vascular segmentation and dimension calculation methods.

Keywords: Fractals; Retina; Diagnostic techniques and procedures; Biometry

---

 

 

INTRODUÇÃO

"A geometria fractal da natureza"

"Nuvens não são esferas, montanhas não são cones, linhas costeiras não são círculos, cascas de árvores não são suaves e nem mesmo a luz caminha em linha reta"

(Mandelbrot, Fractal Geometry of Nature, 1982)⁽¹⁾

A palavra fractal, cunhada por Benoit Mandelbrot, foi originada do radical fractus, particípio passado do verbo latino frangere, que quer dizer quebrar, produzir pedaços irregulares, em alusão à forma irregular e fragmentada dos objetos ditos fractais⁽¹⁾. Só recentemente introduzido na ciência, o termo carece ainda de uma definição rigorosa, universalmente aceita.

Segundo o próprio Mandelbrot, fractais são conjuntos em que a Dimensão de Hausdorff-Besicovitch excede a dimensão topológica⁽¹⁾ (o que será mais bem explicado adiante). Esta definição, por não oferecer ao médico uma idéia do que seriam os fractais, não é a melhor no presente contexto e, assim, na inexistência de uma definição precisa, considerar-se-ão os fractais como padrões ou estruturas gerados pela repetição de uma lei de construção e que apresentam complexidade crescente, na medida em que são observados em escalas menores. Mais ainda, os fractais são reconhecidos por compartilharem de algumas características, tais como^(2-3): a) auto-similaridade; b) lei de potência; c) propriedades estatísticas anômalas; d) dimensão fractal, em geral não inteira; e) lei ou algoritmo de construção.

A auto-similaridade significa que cada parte menor do objeto ou processo fractal se assemelha ao todo. Para exemplificar, considere-se um fractal bastante conhecido: a "curva de von Koch", criada pela substituição de um segmento de reta por quatro outros segmentos com um terço do comprimento original, conforme explicitado na figura 1. O fractal é o resultado da repetição ad infinitum desse processo, que, se construído sobre um triângulo eqüilátero, dá origem à "ilha" ou "floco de neve" de Koch⁽⁴⁾.

 

 

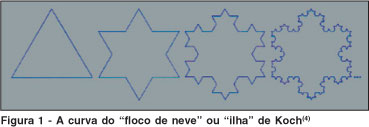
O floco de neve de Koch é uma figura complexa, com grande riqueza de detalhes, não sendo possível mapear todos os seus pontos, como na Geometria euclidiana e cartesiana clássicas, porque, a cada etapa, novas anfractuosidades aparecem onde antes se divisava apenas um segmento de reta⁽¹⁾. Mas é possível descrever a sua lei, ou algoritmo de criação^(1,5).

Outra característica interessante reside no fato de que, embora encerre uma área finita, o seu perímetro, de maneira aparentemente paradoxal, é infinito⁽⁴⁾. Propriedade em parte compartilhada por uma série de estruturas nos seres vivos, como os pulmões, os intestinos, a malha trabecular do olho etc., cuja estrutura imbricada e repleta de saliências e reentrâncias se mantém da escala macroscópica até a celular, aumentando as superfícies de trocas, sem aumento do volume do órgão⁽⁶⁾.

A resposta mais adequada à pergunta acerca do tamanho dessas estruturas biológicas é: não existe nenhum tamanho característico, a não ser que se especifique a escala de medida. Caso contrário, a variância das medidas tende ao infinito e nenhuma média existe: as propriedades estatísticas são anômalas. Tudo o que se pode fazer é quantificar como as medidas crescem na medida em que o fractal é observado com maior riqueza de detalhes, o que é expresso pela dimensão de auto-similaridade (ou dimensão fractal)⁽³⁾.

Quando um objeto geometricamente auto-similar é examinado com maior resolução, pequenas réplicas adicionais do todo podem ser distinguidas. A dimensão de auto-similaridade descreve quantas novas peças similares ao todo são distinguidas, na medida em que a resolução aumenta. Se, ao aumentar a resolução por um fator F (o que equivale a dizer que a escala de medida é dividida por esse fator F), passarem a ser observadas N peças similares ao original, então pode ser afirmado que a dimensão de auto-similaridade é dada por⁽⁷⁾:

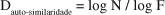
O que, expresso sob a forma de uma lei de potência, é o mesmo que:

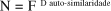
Com efeito, ao examinar a curva de Koch com resolução crescente (Figura 2), observa-se que, a cada iteração, quando se diminuem os segmentos que a compõe por 1/3 (F=3), podem ser observados mais quatro segmentos iguais ao original (N=4). Se a resolução é aumentada e se observam segmentos com 1/9 do tamanho original, então agora podem ser distinguidos N=16 segmentos similares ao original⁽⁵⁾. Donde resulta que a dimensão de auto-similaridade da curva de Koch é:

 

 

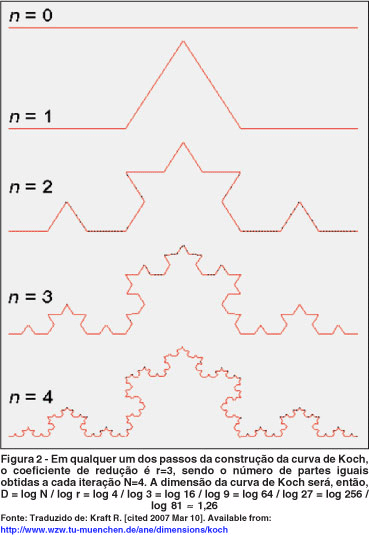
D_{auto-similaridade} = log N / log F = log 4 / log 3 = log 16 / log 9 = 1,2619

Isto significa que a curva de Koch, por ser mais "enrugada" que o segmento de reta, ocupa mais espaço do que uma simples linha reta (dimensão 1), mas menos espaço do que uma superfície (que tem dimensão 2). Note-se ainda que a curva de Koch tem dimensão topológica igual a 1, visto que pode ser dividida por um ponto (dimensão zero). Como a sua dimensão fractal de auto-similaridade (e, por conseguinte, a dimensão de Hausdorff) é maior que a topológica, então, pela definição de Mandelbrot⁽¹⁾, a curva de Koch é um fractal.

Objetos naturais dotados de características fractais não exibem auto-similaridade geométrica estrita, de tal maneira que não é possível calcular as suas dimensões fractais assim como foi feito para a curva de Koch. Porém, apresentam auto-similaridade estatística quando examinados em diversas escalas^(6,8), crescendo também segundo uma lei de potência, o que permite que sejam feitos os cálculos das suas dimensões.

Um dos métodos de cálculo de dimensão utilizados para objetos naturais é a dimensão de capacidade, muito próxima da dimensão de Hausdorff-Besicovitch e que será usada em lugar desta última (cujo formalismo matemático está fora do escopo deste trabalho). A dimensão de capacidade é obtida cobrindo-se com N(r) esferas o objeto fractal, onde N(r) é o número mínimo de esferas de raio r necessárias para cobrir todos os pontos do objeto fractal. Assim, na medida em que o raio dessas esferas diminui (1/r aumenta), maior será o número N(r) de pequenas esferas, necessário para que se cubra o objeto. Repete-se o procedimento com esferas de diferentes tamanhos e traça-se um gráfico log-log de N(r) em função de 1/r (raio das esferas). A inclinação desse gráfico é a dimensão de capacidade, que pode ser definida, formalmente, através da seguinte expressão⁽²⁾:

Há outros métodos para o cálculo da dimensão fractal de objetos naturais baseados em princípios semelhantes e os métodos empregados neste estudo serão mais bem descritos na seção Métodos.

Teleologia e morfogênese

Como codificar com apenas 100 mil genes, boa parte deles sem uma "função" específica, a existência de 100 bilhões de neurônios, formando uma rede com um quatrilhão de sinapses? Como codificar as sinapses dos 120 milhões de fotorreceptores, através das células bipolares, com o milhão e meio de células ganglionares, formando o verdadeiro extrator de caracteres que é a retina e traçar as vias paralelas através do corpo geniculado até o córtex cerebral e, aí, organizar as hiper-colunas de dominância ocular, responsáveis apenas por uma etapa primária da visão? Como desenhar ainda, com este número limitado de genes, os diversos tipos de células e tecidos e o intrincado padrão das árvores vasculares dos diversos órgãos? E como garantir que as árvores vasculares e os circuitos neurais assim pré-concebidos se ajustem às necessidades do organismo e às contingências do meio?

A solução para o problema do ajuste da rede é fazer com que seja realimentada (em sua construção e em seu funcionamento) com a informação acerca do seu "desempenho" pretérito: permitir que o fim "realimente" os meios. O melhor parâmetro é, portanto, a própria concentração tissular do oxigênio.

 

figura 3

 

A solução para o problema da economia de genes é a construção fractal: escrever, com o limitado "hardware" genético, um "software" básico, cuja iteração, isto é, cuja repetição seriada, faça emergir a complexidade. Com o detalhe de que é possível, com o uso de um algoritmo fractal, deixar espaço para pequeno grau de aleatoriedade⁽¹⁾. O que, associado à maquinaria genética da apoptose, torna possível o remodelamento segundo as contingências e as necessidades dos tecidos, ajustando, por exemplo, a arquitetura vascular à demanda tissular por oxigênio.

Da seleção natural, resulta a aparente teleologia dos seres vivos. A seleção natural é o "relojoeiro cego"; e "Ele" tem os seus métodos: construção fractal e seleção por apoptose é a provável base de toda a morfogênese biológica.

A Geometria fractal e a vasculatura retínica

Recentemente, alguns trabalhos têm proposto explícita ou implicitamente que, sendo a vasculatura retínica um fractal, as dimensões fractais seriam a medida natural da neovasogênese^(9-17).

Entretanto, a análise desses estudos mostra que não houve padronização do método de obtenção, nem do método de tratamento das imagens, assim como não houve padronização do método de segmentação da árvore vascular, nem do método de cálculo das suas dimensões, com grande variabilidade inter e intra-estudos.

Mais importante ainda é o fato de que a etapa primordial durante a criação de "softwares" para o diagnóstico automatizado das doenças retínicas (e também para a análise fractal da sua árvore vascular) consiste em conseguir filtrar, da imagem retinográfica, apenas aquilo que corresponde aos vasos^(18-21), processo denominado segmentação vascular. Não obstante esse processo de segmentação altere diretamente a "imagem da árvore vascular" a ser analisada⁽²²⁾, nenhum estudo foi dedicado a avaliar o efeito dos métodos de segmentação sobre a estimação das dimensões fractais da vasculatura, havendo a possibilidade de que as diferenças nos valores das dimensões fractais obtidas nos estudos prévios seja apenas efeito do uso de diferentes métodos de segmentação, ou mesmo que eventuais diferenças entre as dimensões fractais dos vasos de pessoas "normais" em relação aos de "doentes" sejam introduzidas pelo método de segmentação vascular, ao invés de refletirem reais diferenças entre as suas árvores vasculares.

Sendo assim, este trabalho objetivou determinar se a estimação das dimensões fractais da vasculatura retínica é dependente dos métodos de segmentação vascular e dos métodos de cálculo de dimensão.

 

MÉTODOS

As árvores vasculares de dez retinografias de fundos de olhos normais, de pacientes entre 18 e 38 anos, foram extraídas mediante segmentação manual por um pesquisador e por quatro métodos de segmentação automática, cujas estratégias computacionais adotadas foram denominadas "verification-based multithreshold"⁽²³⁾, "pixel classification"⁽²⁴⁾, "scale-space analysis"⁽²⁵⁾ e "ridge based vessel detection"⁽²⁶⁾. A figura 4 mostra as árvores vasculares obtidas quando uma mesma retinografia foi submetida a cada um dos diferentes métodos de segmentação.

Estas imagens podem ser consultadas na página eletrônica do Image Sciences Institute, http://www.isi.uu.nl e a descrição e dos algoritmos utilizados por esses métodos de segmentação, fora do escopo deste trabalho, está explicitada na página eletrônica mencionada e nas referências especificadas, em que estão detalhados os métodos computacionais e os resultados obtidos^{(23-25,27-29)}.

As árvores vasculares obtidas por cada um dos métodos de segmentação foram submetidas ao cálculo das suas dimensões por "contagem de caixas", de "informação" e de "massa-raio".

Para o método de "contagem de caixas", várias grades quadrangulares com comprimento do lado da caixa (r) variável foram superpostas às imagens, o maior tamanho de caixa correspondendo a um quarto da altura ou largura da imagem (o que fosse menor) e diminuindo-se o tamanho das caixas (escala de medida) segundo progressão geométrica, o que foi conseguido dividindo-se o tamanho das caixas por 1,3 a cada etapa. Cada grade foi girada em passos de 10 em 10 graus, contando-se o número de caixas ocupadas N(r) pela imagem dos vasos e anotando-se o número mínimo de caixas ocupadas, entre as nove medidas obtidas ao girar a grade, para cada um dos tamanhos de caixa (escalas).

Os valores do logaritmo neperiano de N(r) foram representados em função do logaritmo neperiano do inverso do comprimento do lado das caixas (1/r) e submetidos à regressão linear pelo método dos mínimos quadrados. O coeficiente de primeiro grau da função resultante é a dimensão fractal por "contagem de caixas".

Para a obtenção da dimensão de informação, foi contado o número de pixels presentes em cada caixa, calculando-se a dimensão de informação através da seguinte expressão:

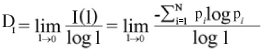
Onde 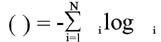é denominada entropia de Kolmogorov e p_i é a probabilidade de encontrar-se um ponto do objeto ou processo fractal em uma circunferência de raio l, quando l tende a zero.

A dimensão de massa-raio foi obtida construindo-se círculos de diferentes raios (centrados no disco óptico) e contando-se o número de pixels (massa) dentro de cada um desses círculos. Os valores do logaritmo da Massa em pixels, M (r) – que é o numero de pixels dentro do círculo de raio (r) – foram representados em função do logaritmo de r (usando-se os mesmos valores de r utilizados para os dois outros métodos de cálculo) e submetidos à regressão linear pelo método dos mínimos quadrados. O coeficiente de primeiro grau foi considerado como a dimensão de "massa-raio" da árvore vascular.

Os valores de dimensão fractal das árvores vasculares dos 10 olhos, obtidas por cada um dos métodos de segmentação, foram submetidos ao teste de Shapiro-Wilks, a fim de averiguar eventual distribuição gaussiana. Como isto foi confirmado, foram submetidos ao teste t para dados pareados, a fim de comparar os valores das dimensões fractais entre os diversos grupos, dois a dois.

Considerando-se que a caracterização da distribuição de amostras pequenas (com n menor que 30) como sendo gaussiana é motivo de controvérsias⁽³⁰⁾, procedeu-se à comparação entre os grupos também mediante o uso de teste não-paramétrico para dados pareados (teste de Wilcoxon para dados pareados). O nível de significância adotado foi a=0,05 e os valores p apresentados são os obtidos para o teste paramétrico, optando-se por indicar o valor p do teste não-paramétrico somente onde os resultados dos testes paramétrico e não-paramétrico fossem conflitantes, o que, adianta-se aqui, não ocorreu durante a comparação de nenhum dos grupos entre si.

 

RESULTADOS

Os valores das dimensões fractais por "contagem de caixas", de "informação" e de "massa-raio" seguiram uma distribuição gaussiana para todos os métodos empregados e encontram-se discriminados nas tabelas 1, 2 e 3, respectivamente. As árvores vasculares apresentaram menores valores de dimensão quando segmentadas pelos métodos "pixel classification" e "ridge-based detection" e os maiores valores de dimensão quando segmentadas manualmente ou por "scale-space". Houve diferença estatisticamente significativa entre os valores das dimensões fractais por "contagem de caixas" e de "informação", quando os vasos foram segmentados manualmente ou pelas técnicas de "pixel classification", "ridge-based detection" ou "multithreshold", porém não houve diferença estatisticamente significante entre os valores de dimensão fractal, quando os vasos foram segmentados manualmente ou pela técnica automática de "scale-space".

Os valores de dimensão de informação foram maiores que os valores de dimensão estimados por contagem de caixas para as árvores vasculares de todos os pacientes e para todos os métodos de segmentação empregados e essa diferença foi estatisticamente significativa (p<0,01), para o nível de significância adotado.

O cálculo da dimensão fractal pelo método de "massa-raio" apresentou menor reprodutibilidade em relação ao cálculo das dimensões de "informação" e por "contagem de caixas", o que pode ser comprovado pela observação de que a variância da dimensão de "massa-raio" foi significativamente maior que a observada para os métodos de "informação" e por "contagem de caixas".

 

DISCUSSÃO

Comparação entre os métodos de segmentação

Como se pode depreender dos resultados apresentados nas tabelas 1, 2 e 3, a estimação da dimensão fractal foi dependente do método de segmentação empregado. Este resultado coloca um problema para o uso das dimensões fractais, sugerido em outros trabalhos^{(9-11,13,15-16)} como possível parâmetro em tentativas futuras de diagnóstico computadorizado das doenças vasculares retínicas.

Com efeito, é possível que a estimação das dimensões fractais seja mais sensível a diferenças entre os métodos de segmentação do que as diferenças reais entre os vasos, introduzidas por eventual doença.

É necessário, portanto, que qualquer tentativa de análise fractal e eventual comparação entre olhos "sadios" e "doentes" se fundamente num método padronizado de segmentação vascular. Por esse motivo é que todos os métodos foram comparados com a segmentação manual, considerada o padrão áureo^(24,31). O método computacional "scale-space" não apresentou diferença em relação à segmentação manual, sugerindo-se que seja preferencialmente utilizado quando se desejar segmentar os vasos da retina para fins de cálculo das suas dimensões fractais.

Outro problema que necessita investigação consiste na possibilidade de que alterações introduzidas pela doença alterem a eficácia dos softwares na segmentação dos vasos. Com efeito, exsudatos duros criam uma alteração nos gradientes (nas derivadas dos valores de brilho) das imagens, podendo ser equivocadamente classificados como "vasos" pelos softwares de segmentação^(24,31).

As hemorragias retínicas, por sua vez, podem produzir dois efeitos paradoxais: diminuem a possibilidade de observação dos vasos, cuja imagem pode ficar oculta sob elas, mas, por outro lado, adicionam áreas de aumento no gradiente das imagens, podendo ser, também, equivocadamente segmentadas como "vasos"^{(19,24,29,31)}.

Aqueles que tentem desenvolver softwares para o diagnóstico computadorizado das doenças vasculares da retina podem tentar reverter estas dificuldades em proveito próprio.

Assim, é possível que, após a submissão da imagem retínica ao software de segmentação, pixels que não estejam colocados de maneira "alinhada", sejam subtraídos da árvore vascular e classificados como "hemorragia", "exsudatos" ou "manchas algodonosas". Em imagens coloridas, sejam elas do tipo RGB, cor de 8 bits ou "full color", os gradientes de cada canal de cor podem ser usados separadamente (e eventualmente associados a operações de Morfologia matemática) para se classificarem esses três sinais de doença.

Do que foi exposto, resta dizer que as dimensões fractais expressam alterações do conjunto dos vasos retínicos. Sua análise em conjunto com outras operações, tais como a extração computadorizada de sinais oftalmoscópicos de doença e o cálculo da tortuosidade e calibre vasculares, poderá contribuir para o desenvolvimento de softwares que se prestem ao diagnóstico automatizado das doenças vasculares da retina.

Comparação entre os métodos de cálculo de dimensão

Durante a padronização do método de cálculo das dimensões fractais foi escolhido variar o tamanho das caixas em progressão geométrica, iniciando-se com uma caixa mínima de 2 pixels (equivalente aos menores capilares que podiam ser observados, com cerca de 40 micra) e multiplicando-se este valor por 1,3 a cada etapa. Isso foi feito para que se obtivessem intervalos logarítmicos iguais para a subseqüente regressão linear.

Por definição, a dimensão "de caixas" ("box dimension") é obtida pela "melhor cobertura", ou seja, a cobertura do objeto com o menor número possível de "caixas" de um determinado tamanho linear (r). Como a sobreposição de uma grade quadrangular não permite essa "cobertura ótima", a grade foi girada, anotando-se, para cada tamanho de caixa, o menor valor de N(r), de maneira a aproximar o valor de dimensão assim obtido, dimensão por "contagem de caixas" ("grid dimension") do valor "ideal" que se obteria pela "cobertura ótima" do objeto⁽³²⁾.

A variância dos valores da dimensão de "massa-raio" foi maior que a obtida para os outros dois métodos. Esta maior variância foi observada em virtude de o método massa-raio ser bastante dependente do ponto a partir de onde são centrados os círculos concêntricos para o cálculo da "massa" (em pixels) da figura. Neste estudo, esse ponto de partida foi fixado no disco óptico, uma vez que a sua colocação no centro da imagem fá-lo-ia coincidir com a zona avascular foveal, o que implicaria na contagem de poucos pixels para os círculos inicias. Destarte, o crescimento da "massa" em pixels com os círculos subseqüentes seria anormalmente superestimado, retornando valores absurdos de dimensão, tais como D>4,00, por exemplo. Maior variância dos valores de dimensão calculados pelo método "massa-raio" também foi observada em outro trabalho⁽¹³⁾. Essa maior variância foi compatível com o fato de que o método de massa-raio é mais adequado para caracterização de objetos que mantém simetria em relação a um ponto central, o que não é o caso das imagens retinográficas⁽³²⁾. Tudo isso torna os resultados do método de cálculo "massa-raio" de menor reprodutibilidade na determinação da dimensão fractal da árvore vascular retínica, sugerindo-se que, doravante, seja preterido em favor dos métodos de "informação" e "por contagem de caixas".

Como a dimensão por contagem de caixas não leva em conta o número de pixels em cada caixa, procedeu-se também, neste estudo, ao cálculo da dimensão de informação, que considera o "peso" (quantidade de pixels) de cada caixa e é mais adequada para a caracterização de fractais não homogêneos em sua invariância de escala^(2,32). Os dados obtidos poderão ser usados futuramente na investigação de possível "multifractalidade" da árvore vascular.

Projeção da imagem retínica no "plano" da fotografia

Importante consideração a fazer, no que respeita ao cálculo das dimensões fractais da árvore vascular, é a de que se está examinando a representação, no plano, de uma imagem que corresponde, na verdade, à "casca" de uma superfície aproximadamente esférica. Esta transformação topológica da "casca" de uma esfera num plano já foi extensivamente tratada por Besicovitch e, mais recentemente, por Falconer⁽³²⁾. A dimensão fractal da projeção de um objeto não é alterada, desde que essa dimensão seja menor que a dimensão Euclidiana do espaço em que é projetada^(1,32). Como a dimensão fractal da vasculatura retínica, em torno de 1,5, é menor que a dimensão euclidiana do espaço em que é projetada (o plano, com dimensão = 2), então a dimensão fractal calculada não é alterada.

Dimensões fractais inferiores às relatadas em outros estudos

Os valores de dimensão fractal obtidos no presente estudo foram significativamente inferiores aos obtidos em estudos prévios^{(10-11,13-17)}.

Importa questionar se os valores de dimensão fractal da árvore vascular poderiam ter sido "desviados" para baixo em virtude de um possível "efeito das margens" da imagem, uma vez que foram analisadas áreas retangulares de imagens retinográficas circunferenciais, estando as margens da imagem "livres" de vasos. Importa questionar também se a restrição da análise fractal a uma região de interesse circunferencial geraria valores mais altos de dimensão, anulando um eventual "efeito das margens", o que será objeto de um estudo posterior pelos autores.

Por hora, vale lembrar que nenhuma medida foi utilizada nos estudos anteriores em análise fractal da retina para anular esse possível "efeito das margens" e que, portanto, a diferença entre os valores de dimensão obtidos no presente estudo e os obtidos nos estudos anteriores não se deve a esse aludido "efeito das margens".

É provável que os valores mais elevados de dimensão obtidos nos estudos anteriores seja resultado do emprego do método de cálculo de "massa-raio"^(13,17), que como já foi comentado, pode originar valores equivocadamente altos, se os círculos para contagem da "massa" são colocados na zona avascular foveal. Porém não há descrição específica, nesses estudos, a respeito do tamanho e localização dos círculos utilizados.

Outra possível explicação para a obtenção de valores mais altos de dimensão em alguns estudos anteriores reside na utilização, nesses estudos^(9,13-15,17), de imagens de angiofluoresceinografia, em que o vazamento de contraste, ou mesmo a hiperfluorescência a partir da cório-capilar,⁽³³⁾ pode induzir à segmentação equivocada de alguns pixels como "vasos", desviando para cima o cálculo da dimensão fractal da vasculatura.

Multifractalidade?

A este respeito, importa observar que simples fractais gerariam um padrão de grandes vazios quando vistos em grandes escalas⁽¹⁶⁾ e de vazios muito pequenos quando vistos em escalas muito pequenas, de tal sorte que o padrão possivelmente teria, do ponto de vista teleológico, poucas "vantagens econômicas" em termos de oferta de oxigênio e nutrientes. Espera-se, pois, que a árvore tenha características distintas, quando comparados os padrões dos grandes vasos com aquele dos capilares, o que é compatível com o fato de que artérias e capilares devem cumprir funções complementares, mas diferentes⁽³⁴⁾. É esperado, portanto, que a estrutura siga um padrão multifractal.

Some-se a isso a demonstração dada pelo próprio Mandelbrot⁽¹⁾ de que "árvores" originadas por ramificação dicotômica podem aumentar a sua dimensão fractal até se tornarem estruturas do tipo "space-filling", através de uma simples transformação topológica, que consiste na alteração do ângulo das ramificações. Assim, aumentando progressivamente este ângulo até 90 graus, pode-se obter uma curva que preenche totalmente o plano^(1,5).

É possível, portanto, que os capilares formem, na verdade, uma estrutura do tipo "space-filling"^(1,32), o que é compatível com a necessidade de levar nutrientes e drenar os subprodutos do metabolismo celular por todo o tecido. Sendo assim, é de se esperar que os capilares se disponham como uma rede do tipo "quasi-regular lattice"^(1,32), com poros não superiores a um determinado valor e com capilares próximos a cada célula do tecido. Isso poderá ser investigado mediante o exame dos vasos retínicos em cortes histológicos, devendo-se esperar que a dimensão fractal tenda a dois, ou seja, a estrutura preencha totalmente o "plano" da retina, quando forem usados tamanhos de caixa não inferiores ao tamanho dos "poros" da rede vascular.

A hipótese de que os vasos retínicos sigam um padrão multifractal já foi sugerida em outros trabalhos^(35-36). Entretanto, a adequada análise multifractal necessita que o tamanho do "foreground", ou seja, da parte da imagem segmentada como "vaso" seja maior que um milhão de pixels^(1,32), valor bem acima do encontrado neste trabalho e nos trabalhos supra-citados. Além disso, os aparelhos de retinografia habitualmente utilizados fornecem imagens cujo tamanho e resolução estão bem abaixo^(37-38) da necessária para a realização de uma adequada análise "multifractal".

São as dimensões fractais a medida natural da neovasogênese?

O argumento em que se baseiam os trabalhos que defendem o uso das dimensões fractais como o "parâmetro natural" para o diagnóstico da neovasogênese não é válido. De fato, esses trabalhos afirmam implícita ou explicitamente que "sendo os vasos retínicos fractais, a dimensão fractal é a medida natural da neovasogênese". Afirmação que erra duas vezes: na matéria e na forma, isto é, nos dados e no raciocínio.

Erra nos dados porque considera como fato comprovado a proposição "os vasos retínicos são fractais", proposição que não foi definitivamente comprovada; e erra no raciocínio porque, ainda que os vasos retínicos fossem fractais, disso não decorreria que as dimensões fractais fossem a sua medida natural, menos ainda a medida natural da neovasogênese.

O que foi dito acima pode ser mais bem evidenciado dissecando-se o argumento utilizado, em que se tenta montar um polissilogismo onde a conclusão de um silogismo serve de premissa menor para o que lhe sucede. A seqüência de silogismos é:

Todo objeto cujo gráfico bi-logarítmico se ajusta à reta é fractal;

Ora, os gráficos bi-logarítmicos dos vasos retínicos se ajustam à reta;

Logo, a vasculatura retínica é fractal.

Segundo silogismo:

Todo objeto fractal tem como medida natural as suas dimensões fractais;

Ora, a vasculatura retínica é fractal;

Logo, as dimensões fractais são a medida natural da neovasogênese.

O primeiro silogismo é inválido porque não teve a sua premissa maior definitivamente demonstrada. Sua conclusão, inválida, é usada como premissa menor do segundo silogismo, invalidando-o de saída. Ademais, também a premissa maior do segundo silogismo – "todo objeto fractal tem como medida natural a sua dimensão fractal" – carece de comprovação. Ou seja, ainda que se provasse serem os vasos retínicos fractais (o que não foi definitivamente estabelecido), isso não implicaria necessariamente que as dimensões fractais fossem a sua medida natural, haja vista a possibilidade de existirem outros parâmetros que poderiam eventualmente melhor caracterizá-los. Faz-se assim um silogismo non sequitur, ao admitir, como verdade consabida, uma premissa que, camuflada sob a forma de entimema, não teve a sua veracidade estabelecida. Como se isso tudo não bastasse, ainda pior é a mudança de objeto – de vasculatura retínica para neovasogênese – que é feita, sem nenhuma explicação, na passagem da premissa menor do segundo silogismo à sua conclusão.

Em suma, pode-se afirmar que embora as dimensões fractais dos vasos retínicos possam ser usadas como auxiliar em métodos para o diagnóstico automatizado das doenças retínicas, a afirmação de que as referidas dimensões são a medida natural da neovasogênese carece de sustentação. A este respeito, vale lembrar que outros parâmetros poderiam ser eventualmente mais adequados, seja para o diagnóstico, seja para o entendimento da neovasogênese.

No que concerne ao melhor entendimento da neovasogênese, lembre-se que um dos aspectos fundamentais dos fractais é o de serem construídos segundo um algoritmo. Assim, se é desejado compreender a lei morfogenética da vasculatura, a lei de formação do fractal, será fundamental, entre outras coisas, estabelecer as relações entre: os calibres dos vasos parentais e os de seus ramos, os ângulos de bifurcação e os fatores hemodinâmicos, os comprimentos dos ramos vasculares e os dos vasos parentais; e, enfim, elaborar um programa cuja iteração faça emergir a "imagem" da vasculatura.

Já no que tange à criação de métodos de diagnóstico automatizado, embora as dimensões fractais possam servir como parâmetro auxiliar, cumpre lembrar que os sinais clínicos de doença, já consabidos pelos oftalmologistas, deverão ser empregados pelos métodos computacionais de diagnóstico, uma vez que é esperado que, para que ocorram mudanças nas dimensões fractais da vasculatura, é preciso que ocorram modificações acentuadas na arquitetura da árvore vascular inteira, enquanto os sinais iniciais de doença são freqüentemente mais localizados^(33,39), o que torna as dimensões fractais possivelmente menos sensíveis na detecção dos sinais iniciais das doenças.

Assim, apesar de a hipótese do padrão fractal para as células e vasos da retina ser atraente e de os autores serem levados a crer que toda a modelagem em Biologia se dê por construção fractal e seleção por apoptose, é preciso muita parcimônia ao se afirmar que os vasos retínicos seguem um padrão fractal. Objetos fractais mantêm invariância quando observados ao longo de várias escalas e, se isto é verdade para o caso aqui posto, o é para uma faixa limitada de escalas, não mais do que duas dezenas.

Com efeito, o fato de os valores de N(r) obedecerem a uma lei de potência e originarem uma função linear quando log_n N(r) é plotado em função de log_n 1/r é condição necessária, mas não suficiente para caracterizar algo como fractal. Não deve ser visto jamais como "prova" do aspecto fractal dessa estrutura (em que pese a inadequação do uso do vocábulo "prova" em ciência) e as medidas de dimensão aqui tratadas devem ser vistas apenas como formas de quantificar a maneira pela qual estes vasos preenchem o espaço, ou a maneira como crescem em complexidade quando vistos em escalas cada vez menores.

Portanto, se é pretendido averiguar o valor das dimensões fractais para o diagnóstico automatizado, será importante realizar trabalhos que comparem, por um método padronizado, as dimensões fractais das árvores vasculares "sadias" com as de pessoas com doença vascular retínica. Este esforço deve ser levado a cabo com a perspectiva de que a Geometria Fractal, por descrever as leis morfogenéticas de estruturas complexas, possa vir a ser utilizada na modelagem matemática da vasogênese e na criação de métodos de diagnóstico automatizado das doenças retínicas, metas que, alcançadas, teriam grande impacto no campo da prevenção da cegueira^(19,22).

 

CONCLUSÃO

A estimação das dimensões fractais da vasculatura retínica foi dependente tanto dos métodos de segmentação vascular, quanto dos métodos de cálculo de dimensão utilizados.

 

REFERÊNCIAS

1. Mandelbrot BB. The fractal geometry of nature. New York: WH Freeman; 1982.        

2. Bassingthwaighte JB, Liebovitch LS, West BJ. Fractal physiology. New York: Oxford University Press; 1994.        

3. Iannaccone PM, Khokha MK. Fractal geometry in biological systems: an analytical approach. Boca Raton, FL: CRC Press; 1996.        

4. Peitgen H-O, Richter PH. The beauty of fractals: images of complex dynamical systems. Berlin; New York: Springer-Verlag; 1986.        

5. Mandelbrot B. Objectos fractais, forma, acaso e dimensão seguido de panorama da linguagem fractal. Lisboa: Gradiva; 1991.        

6. Kaandorp JA. Fractal modelling: growth and form in biology. Berlin: Springer-Verlag; 1994.        

7. West BJ. Fractal physiology and chaos in medicine. Singapore; New Jersey: World Scientific; 1990.        

8. Sandau K, Kurz H. Measuring fractal dimension and complexity—an alternative approach with an application. J Microsc. 1997;186(Pt 2):164-76.        

9. Avakian A, Kalina RE, Sage EH, Rambhia AH, Elliott KE, Chuang EL, et al. Fractal analysis of region-based vascular change in the normal and non-proliferative diabetic retina. Curr Eye Res. 2002;24(4):274-80.        

10. Daxer A. Characterisation of the neovascularisation process in diabetic retinopathy by means of fractal geometry: diagnostic implications. Graefes Arch Clin Exp Ophthalmol. 1993;231(12):681-6.        

11. Daxer A. The fractal geometry of proliferative diabetic retinopathy: implications for the diagnosis and the process of retinal vasculogenesis. Curr Eye Res. 1993;12(12):1103-9.        

12. Daxer A. Mechanisms in retinal vasculogenesis: an analysis of the spatial branching site correlation. Curr Eye Res. 1995;14(4):251-4.        

13. Family F, Masters BR, Platt DE. Fractal pattern formation in human retinal vessels. Physica D. 1989;38:98-103.        

14. Landini G, Misson GP, Murray PI. Fractal analysis of the normal human retinal fluorescein angiogram. Curr Eye Res. 1993;12(1):23-7.        

15. Landini G, Murray PI, Misson GP. Local connected fractal dimensions and lacunarity analyses of 60 degrees fluorescein angiograms. Invest Ophthalmol Vis Sci. 1995;36(13):2749-55.        

16. Masters BR. Fractal analysis of the vascular tree in the human retina. Annu Rev Biomed Eng. 2004;6:427-52.        

17. Mainster MA. The fractal properties of retinal vessels: embryological and clinical implications. Eye. 1990;4(Pt 1):235-41.        

18. Sinthanayothin C, Boyce JF, Williamson TH, Cook HL, Mensah E, Lal S, Usher D. Automated detection of diabetic retinopathy on digital fundus images. Diabet Med. 2002;19(2):105-12.        

19. Teng T, Lefley M, Claremont D. Progress towards automated diabetic ocular screening: a review of image analysis and intelligent systems for diabetic retinopathy. Med Biol Eng Comput. 2002;40(1):2-13.        

20. Usher D, Dumskyj M, Himaga M, Williamson TH, Nussey S, Boyce J. Automated detection of diabetic retinopathy in digital retinal images: a tool for diabetic retinopathy screening. Diabet Med. 2004;21(1):84-90.        

21. Walter T, Klein JC, Massin P, Erginay A. A contribution of image processing to the diagnosis of diabetic retinopathy—detection of exudates in color fundus images of the human retina. IEEE Trans Med Imaging. 2002;21(10):1236-43.        

22. Frame AJ, Undrill PE, Cree MJ, Olson JA, McHardy KC, Sharp PF, Forrester JV. A comparison of computer based classification methods applied to the detection of microaneurysms in ophthalmic fluorescein angiograms. Comput Biol Med. 1998;28(3):225-38.        

23. Jiang X, Mojon D. Adaptive local thresholding by verification-based multithreshold probing with application to vessel detection in retinal images. IEEE Trans Pattern Anal Mach Intell. 2003;25(1):131-7.        

24. Niemeijer MS, Staal J, van Ginneken B, Loog M, Abramoff MD. Comparative study of retinal vessel segmentation methods on a new publicly available database. SPIE Med Imaging. 2004;5370:648-56.        

25. Martínez-Pérez M, Hughes A, Stanton A, Thom S, Bharath A, Parker D. Scale-space analysis for the characterisation of retinal blood vessels. In: Taylor C, Colchester A, editors. Medical Image Computing and Computer-Assisted Intervention - MICCAI'99. 1999. pp.90-7.        

26. Staal J, Abramoff MD, Niemeijer M, Viergever MA, van Ginneken B. Ridge-based vessel segmentation in color images of the retina. IEEE Trans Med Imaging. 2004;23(4):501-9.        

27. Zana F, Kein JC. Segmentation of vessel-like patterns using mathematical morphology and curvature evaluation. IEEE Trans Image Process. 2001;10: 1010-9        

28. Chaudhuri S, Chatterjee S, Katz N, Nelson M, Goldbaum M. Detection of blood vessels in retinal images using two-dimensional matched filters. IEEE Trans Med Imaging. 1989;8(3):263-9.        

29. Soares JV, Leandro JJ, Cesar Junior RM, Jelinek HF, Cree MJ. Retinal vessel segmentation using the 2-D Gabor wavelet and supervised classification. IEEE Trans Med Imaging. 2006;25(9):1214-22.        

30. Zar JH. Biostatistical analysis. 4ht ed. Upper Saddle River, N.J.: Prentice Hall, c1999.        

31. Kirbas C, Quek F. A review of vessel extraction techniques and algorithms. ACM Comput Surv (CSUR). 2004;36(2):81-121.        

32. Falconer K. Fractal geometry: mathematical foundations and applications. 2nd ed. West Sussex; New York: Wiley; c2003.        

33. Ryan SJ. Retina. 2nd ed. St. Louis: Mosby; 1994.        

34. Wise GN, Dollery CT, Henkind P. The retinal circulation. New York: Harper & Row; 1971.        

35. Stosic T, Stosik BD. Multifractal analysis of human retinal vessels. IEEE Trans Med Imaging. 2006;25(8):1101-7.        

36. Zamir M. Fractal dimensions and multifractility in vascular branching. J Theor Biol. 2001;212(2):183-90.        

37. Alezzandrini AA, Nicoli C. [Retinography with fluorescein]. Arch Oftalmol B Aires. 1965;40(11):363-82. Spanish.        

38. Al Sabti K, Raizada S, Wani VB, Al Ajmi M, Gayed I, Sugathan TN. Efficacy and reliability of fundus digital camera as a screening tool for diabetic retinopathy in Kuwait. J Diabetes Complications. 2003;17(4):229-33.        

39. Yannuzzi LA, Guyer DR, Green WR. The retina atlas. St. Louis: Mosby; 1995.        

 

 

Endereço para correspondência:
Av. Presidente Kennedy, 263/202
Jaboatão dos Guararapes (PE) CEP 54420-050
E-mail: [email protected]

Recebido para publicação em 11.08.2005
Última versão recebida em 27.12.2006
Aprovação em 15.01.2007

 

 

Nota Editorial: Depois de concluída a análise do artigo sob sigilo editorial e com a anuência do Dr. Laurentino Biccas Neto sobre a divulgação de seu nome como revisor, agradecemos sua participação neste processo.
Trabalho realizado na Universidade Federal de Pernambuco - UFPE - Recife (PE) - Brasil e Universidade Federal do Rio Grande do Norte - UFRN - Natal (RN) - Brasil.